湘教版七（下）数学第一章整式的乘法单元测试提升卷

试卷更新日期：2026-01-05 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列运算不正确的是（）

A、 $x^{2} \cdot x^{3} = x^{5}$ B、 ${(x^{2})}^{3} = x^{6}$ C、 ${(- 2 x)}^{3} = - 8 x^{3}$ D、 $x^{3} + x^{3} = 2 x^{6}$

查看试题解析
2. 已知 $4^{m} = a$ ， $8^{n} = b$ ，其中 $m$ ， $n$ 为正整数，则 $2^{2 m + 6 n} =$ （）

A、 $a b^{2}$ B、 $a + b^{2}$ C、 $a^{2} b^{3}$ D、 $a^{2} + b^{3}$

查看试题解析
3. 计算 ${(- 1 \frac{1}{2})}^{2023} \times {(\frac{2}{3})}^{2025}$ 的结果等于（）

A、1 B、 $- 1$ C、 $- \frac{9}{4}$ D、 $- \frac{4}{9}$

查看试题解析
4. “白色污染”的主要来源有食品包装袋、泡沫塑料填充物等．已知一个塑料快餐盒的污染面积为 $200 {cm}^{2}$ ，如果30万名游客每人丢弃一个快餐盒，那么造成污染的最大面积用科学记数法表示为（　　）

A、 $6 \times 10^{7} {cm}^{2}$ B、 $0.6 \times 10^{6} {cm}^{2}$ C、 $6 \times 10^{6} {cm}^{2}$ D、 $60 \times 10^{6} {cm}^{2}$

查看试题解析
5. 若 $(x + 1) (x^{2} - 3 a x + a)$ 的乘积中不含 $x^{2}$ 项，则常数a的值为（）

A、3 B、 $- \frac{1}{3}$ C、 $\frac{1}{3}$ D、－3

查看试题解析
6. 若 $x^{2} - k x - 24 = (a x + 12) (x - 2)$ ，则 $k$ 的值是（）

A、10 B、-10 C、 $\pm 10$ D、14

查看试题解析
7. 下列各式能用平方差公式计算的是（）

A、 $(- a + 3) (a - 3)$ B、 $(- a + 3) (3 + a)$ C、 $(- a + 3) (3 - a)$ D、 $(a + 3) (- 3 - a)$

查看试题解析
8. 代数式 $(- x + 3 y) (x + 3 y)$ 化简的结果是（）

A、 $x^{2} + 9 y^{2}$ B、 $- x^{2} + 9 y^{2}$ C、 $x^{2} - 9 y^{2}$ D、 $- x^{2} - 9 y^{2}$

查看试题解析
9. 如图，正方形 ABCD 与正方形 CEFH 的面积和为 58，点 C 在线段 BE 上，点 H 在线段 CD 上，延长 FH 交 AB 于点 G. 若 $B E = 10$ ，则长方形 BCHG 的面积为（）

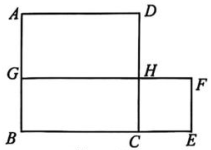A、21 B、24 C、34 D、42

查看试题解析
10. 小明将 ${(2023 x + 2024)}^{2}$ 展开后得到 $a_{1} x^{2} + b_{1} x + c_{1}$ ；小亮将 ${(2024 x - 2023)}^{2}$ 展开后得到 $a_{2} x^{2} + b_{2} x + c_{2}$ ，若两人计算过程无误，则 $c_{1} - c_{2}$ 的值为（）

A、2023 B、2024 C、4047 D、1

查看试题解析

二、填空题（每题3分，共24分）

11. 已知 $4^{m} = 2$ ， $8^{n} = 5$ ，则 $2^{2 m + 3 n} =$ ．

查看试题解析
12. 光的速度约为 $3 \times 1 0^{5} k m / s$ ，太阳光照到地球上要 $5 \times 1 0^{2} s$ ，那么太阳与地球的距离为 $k m$ （用科学记数法表示）．

查看试题解析
13. 若 $(x - 1) (x - 2) = x^{2} + m x + n$ ，则 $n^{m}$ 的值为．

查看试题解析
14. 设 $M = (x + 3) (x - 7) ， N = (x + 1) (x - 5)$ ，则M与N的大小关系为．

查看试题解析
15. 将边长分别为m ， $n (m > n)$ 的两个正方形按如图所示方式摆放，其中点B ， C ， E在同一条直线上，点G在 $C D$ 上，记阴影部分面积为S ．若 $m + n = 10$ ， $m^{2} + n^{2} = 54$ ，则 $S^{2}$ 的值为．

查看试题解析
16. 如图，已知正方形 $A B C D$ 和 $B E F G$ ，点 $A$ ， $B$ ， $E$ 三点共线， $A E = 12.8$ ， $C G = 5$ ，则 $△ A B D$ 与 $△ B E F$ 的面积差是．

查看试题解析
17. 已知 $m + 3 - \frac{2}{m} = 0$ ，则 $m^{2} + \frac{4}{m^{2}}$ 的值为.

查看试题解析
18. 如图，若大正方形与小正方形的面积之差为20，则阴影部分的面积是．

查看试题解析

三、解答题（共8题，共66分）

19. 计算：

(1)、 $2 m \cdot (m n)^{2}$

(2)、 $2 a^{2} b (\frac{1}{2} a b - 3 a b^{2})$ 。

查看试题解析
20. 用乘法公式计算：

(1)、 ${(x - 2 y)}^{2}$

(2)、 $102^{2}$

查看试题解析
21. 先化简、再求值：［（2a+b）² $-$ （2a+b）（2a-6）］÷2b，其中a=2，b=-1.

查看试题解析
22. 在等式的运算中规定：若 $a^{x} = a^{y} (a > 0$ 且 $a \neq 1, x, y$ 是正整数），则 $x = y$ ，利用上面结论解答下列问题：

(1)、若 $9^{x} = 3^{10}$ ，求 $x$ 的值；

(2)、若 $3^{x + 2} - 3^{x + 1} = 162$ ，求 $x$ 的值.

查看试题解析
23. 小明计算一道整式乘法的题 $(2 x - a) (3 x - 2)$ ，由于小明在解题过程中，抄错了第一个多项式中a前面的符号，把“ $-$ ”写成了“ $+$ ”，得到的结果为 $6 x^{2} - x - a b$ ，求a，b的值．

查看试题解析
24. 如图1是一个长为2a，宽为2b的长方形（ $a > b$ ），沿图中虚线前成四块完全一样的小长方形，然后按图2的方式拼成一个正方形.

(1)、图2中阴影部分的正方形的边长是；

(2)、利用图2中阴影部分的面积的两种不同计算方法，写出下列三个代数式 $(a + b)^{2}$ ， $(a - b)^{2}, a b$ 之间的数量关系是.

(3)、利用（2）中的结论，对于实数x、y，当 $x - y = 2, x y = 0.25$ 时，求 $x + y$ 的值.

查看试题解析
25. 若 $n + a = x^{2}$ ， $n - a = y^{2}$ $(n ， a ，$ $x^{2}$ ， $y^{2}$ 是自然数），则称 $x^{2}$ ， $y^{2}$ 为一组“兄弟平方数”，n为这组“兄弟平方数”的“中介数”。
例如： $5 + 4 = 9 = 3^{2}$ ， $5 - 4 = 1 = 1^{2}$ ，则9和1是一组“兄弟平方数”，5是“中介数”.

(1)、试求“兄弟平方数”49和25的“中介数”.

(2)、若“中介数”为52，试求符合要求的“兄弟平方数”

(3)、若“中介数”n，将它分别加上42或减去42，所得的两个数是一组“兄弟平方数”，请直接写出符合要求的所有“兄弟平方数”和相应“中介数”
温馨提示：参考公式х²-y²=（x+у）x-y）

查看试题解析
26. 乘法公式的探究及应用．
数学活动课上，老师准备了若干张如图 $1$ 所示的三种纸片， $A$ 种纸片是边长为 $a$ 的正方形， $B$ 种纸片是边长为 $b$ 的正方形， $C$ 种纸片是长为 $b$ ，宽为 $a$ 的长方形，并用一张 $A$ 种纸片，一张 $B$ 种纸片，两张 $C$ 种纸片拼成了如图 $2$ 所示的大正方形．

(1)、请用两种不同的方法求图 $2$ 中大正方形的面积：（用含 $a ， b$ 的式子表示）
方法 $1$ ：                           ；
方法 $2$ ：                            ．

(2)、观察图 $2$ ，请写出代数式 ${(a + b)}^{2}$ ， $a^{2} + b^{2}$ ， $a b$ 之间的等量关系式                                 ；

(3)、根据（ $2$ ）中的等量关系，解决如下问题：
$①$ 已知 $a + b = 6$ ， $a^{2} + b^{2} = 26$ ，求 $a b$ 的值；
$②$ 已知 ${(x - 2022)}^{2} + {(x - 2024)}^{2} = 48$ ，求 ${(x - 2023)}^{2}$ 的值．

查看试题解析

湘教版七（下）数学第一章 整式的乘法 单元测试提升卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共24分）

三、解答题（共8题，共66分）

湘教版七（下）数学第一章整式的乘法单元测试提升卷