人教版八(下)数学第二十章 勾股定理 单元测试提升卷
试卷更新日期:2026-01-04 类型:单元试卷
一、单选题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. 在中,斜边 , 则的值为( )A、 B、 C、 D、无法计算2. 在正方形网格中,的位置如图所示,到两边距离相等的格点应是( )
 A、点M B、点N C、点P D、点Q3. 如图,在高为 , 坡面长为的楼梯表面铺地毯,地毯的长度至少需要( )
A、点M B、点N C、点P D、点Q3. 如图,在高为 , 坡面长为的楼梯表面铺地毯,地毯的长度至少需要( ) A、 B、 C、 D、4. 我国古代数学名著《九章算术》中记载:“今有户高多余广六尺八寸(一尺等于十寸),两隅相去适一丈(一丈等于十尺).问户高、广各几何?” 意为“现有一扇门,高比宽多了六尺八寸,门的对角线长刚好为一丈.求门的高和宽各为多少?”如图,设户广为x尺,可列出方程( )
A、 B、 C、 D、4. 我国古代数学名著《九章算术》中记载:“今有户高多余广六尺八寸(一尺等于十寸),两隅相去适一丈(一丈等于十尺).问户高、广各几何?” 意为“现有一扇门,高比宽多了六尺八寸,门的对角线长刚好为一丈.求门的高和宽各为多少?”如图,设户广为x尺,可列出方程( ) A、 B、 C、 D、5. 某平板电脑支架如图所示, , 为了使用的舒适性,可调整的大小. 若 , 则AD的长度为( )
A、 B、 C、 D、5. 某平板电脑支架如图所示, , 为了使用的舒适性,可调整的大小. 若 , 则AD的长度为( ) A、12 B、18 C、 D、156. 如图,将有一边重合的两张直角三角形纸片放在数轴上,纸片上的点A表示的数是-2, , 若以点A为圆心,的长为半径画弧,与数轴交于点E(点E位于点A右侧),则点E表示的数为( )
A、12 B、18 C、 D、156. 如图,将有一边重合的两张直角三角形纸片放在数轴上,纸片上的点A表示的数是-2, , 若以点A为圆心,的长为半径画弧,与数轴交于点E(点E位于点A右侧),则点E表示的数为( ) A、 B、 C、 D、7. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为 , 梯子顶端到地面的距离为 . 如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离为 , 则小巷的宽为( ).
A、 B、 C、 D、7. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为 , 梯子顶端到地面的距离为 . 如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离为 , 则小巷的宽为( ). A、 B、 C、 D、8. 如图,在四边形中, , 分别以四边形的四条边为边向外作四个正方形,面积分别为 , , , . 若 , , 则为( )
A、 B、 C、 D、8. 如图,在四边形中, , 分别以四边形的四条边为边向外作四个正方形,面积分别为 , , , . 若 , , 则为( ) A、8 B、10 C、12 D、149. 如图,在底面周长约为6米的石柱上,有一条雕龙从柱底沿立柱表面盘绕2圈到达柱顶正上方,每根华表刻有雕龙的部分的柱身高约16米,则雕刻在石柱上的巨龙至少为( )
A、8 B、10 C、12 D、149. 如图,在底面周长约为6米的石柱上,有一条雕龙从柱底沿立柱表面盘绕2圈到达柱顶正上方,每根华表刻有雕龙的部分的柱身高约16米,则雕刻在石柱上的巨龙至少为( )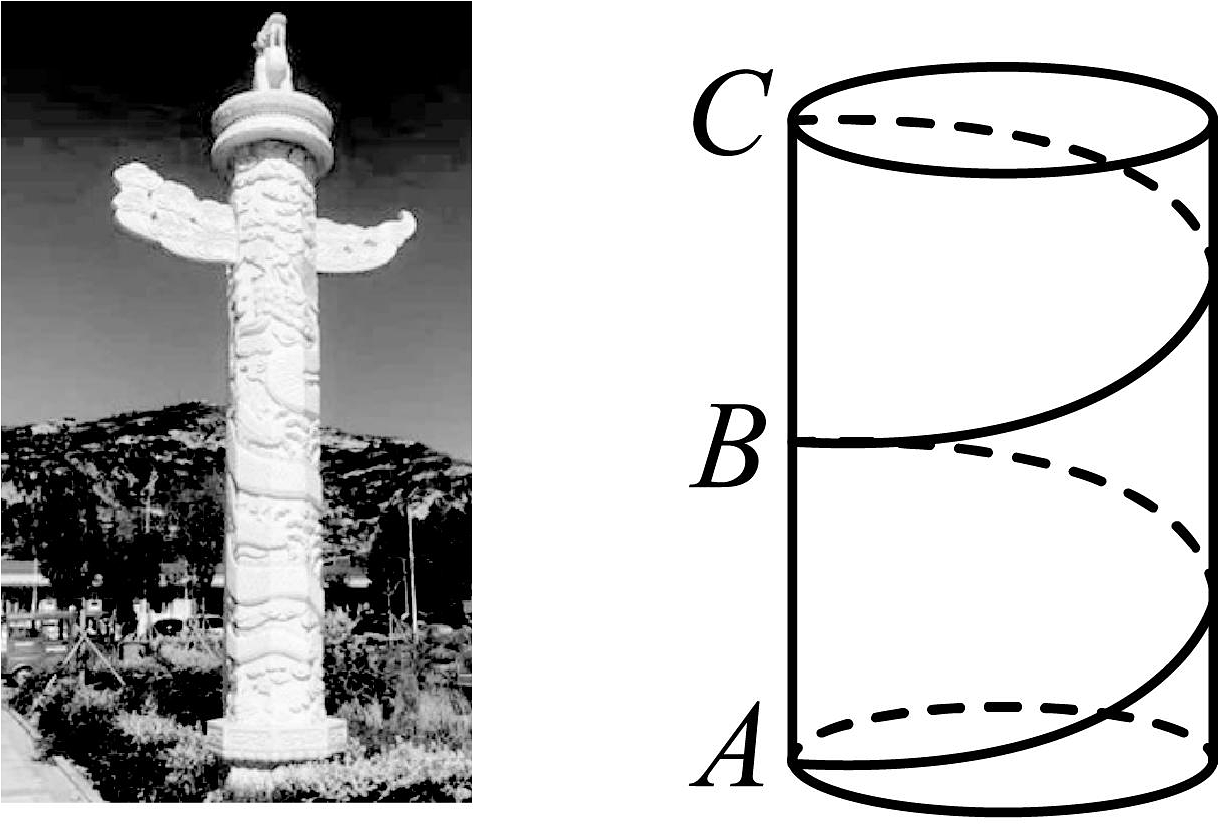 A、20米 B、25米 C、30米 D、15米10. 我国是最早了解勾股定理的国家之一,在《周髀算经》中记载了勾股定理的公式与证明,相传是由商高发现,故又称之为“商高定理”.下列四幅图中,不能证明勾股定理的是( )A、
A、20米 B、25米 C、30米 D、15米10. 我国是最早了解勾股定理的国家之一,在《周髀算经》中记载了勾股定理的公式与证明,相传是由商高发现,故又称之为“商高定理”.下列四幅图中,不能证明勾股定理的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题:本大题共5小题,每小题3分,共15分。
-
11. 如图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若 , , 将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图所示的“数学风车”,则这个风车的外围周长是 .
 12. 如图,每个小正方形的边长为1, , , 是小正方形的顶点,则的度数为 .
12. 如图,每个小正方形的边长为1, , , 是小正方形的顶点,则的度数为 .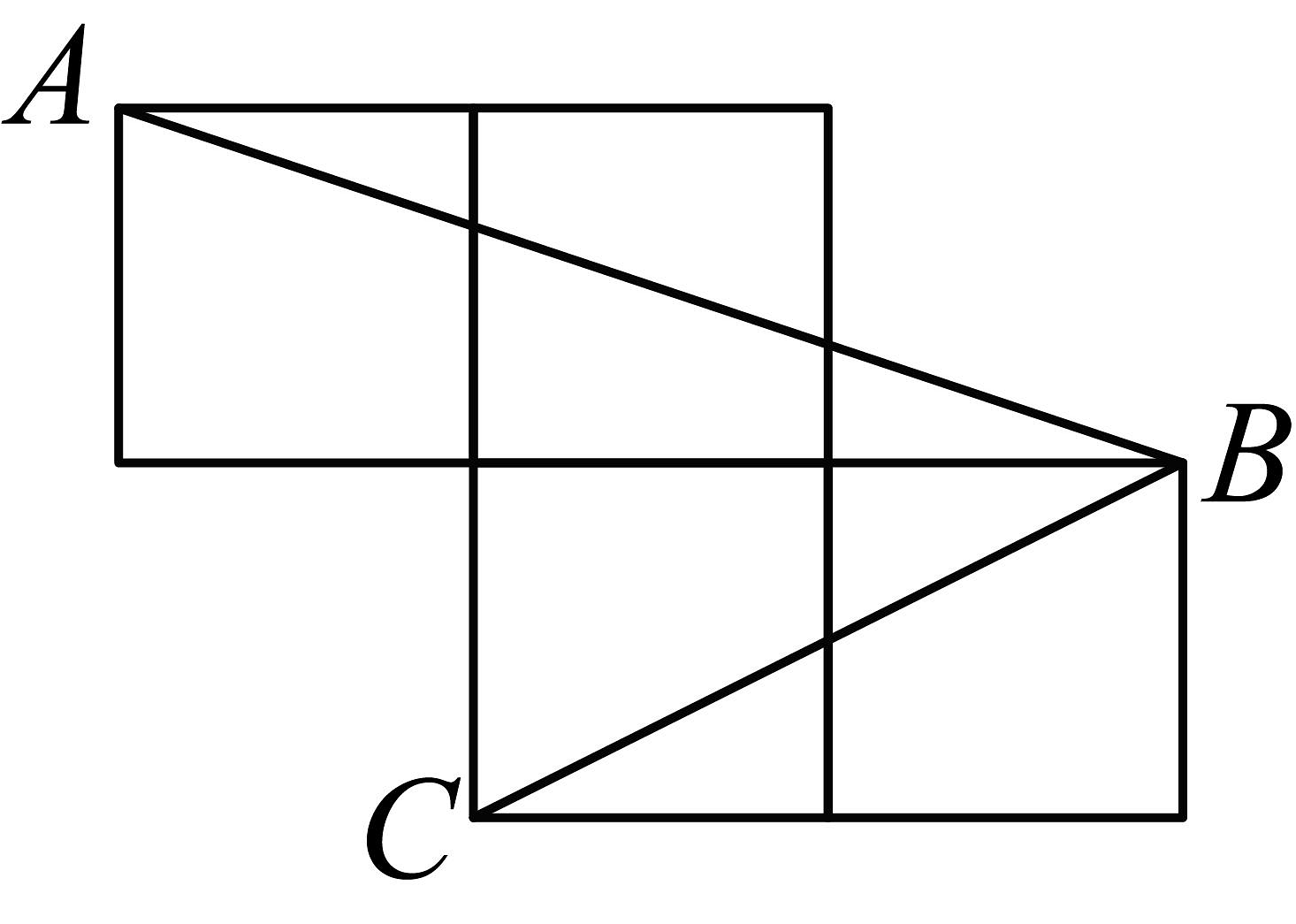 13. 如图,图1是北京国际数学家大会的会标,它取材于我国古代数学家赵爽的“弦图”,是由四个全等的直角三角形拼成.若图1中大正方形的面积为22,小正方形的面积为2,现将这四个直角三角形拼成图2,则图2中大正方形的面积为 .
13. 如图,图1是北京国际数学家大会的会标,它取材于我国古代数学家赵爽的“弦图”,是由四个全等的直角三角形拼成.若图1中大正方形的面积为22,小正方形的面积为2,现将这四个直角三角形拼成图2,则图2中大正方形的面积为 . 14. 如图,在一个长方形草坪ABCD上,放着一根长方体的木块,已知米,米,该木块的较长边与AD平行,横截面是边长为1米的正方形,一只蚂蚁从点A爬过木块到达C处需要走的最短路程是米
14. 如图,在一个长方形草坪ABCD上,放着一根长方体的木块,已知米,米,该木块的较长边与AD平行,横截面是边长为1米的正方形,一只蚂蚁从点A爬过木块到达C处需要走的最短路程是米 15. 如图,已知在中, , , , 是上的一点, , 点从点出发沿射线方向以每秒2个单位的速度向右运动,设点的运动时间为 . 过点作于点 . 在点P的运动过程中,当t为时,能使?
15. 如图,已知在中, , , , 是上的一点, , 点从点出发沿射线方向以每秒2个单位的速度向右运动,设点的运动时间为 . 过点作于点 . 在点P的运动过程中,当t为时,能使?
三、解答题:本大题共8小题,共75分。
-
16. 如图,C 为线段 BD 上一动点,分别过点 B,D 作AB⊥BD,ED⊥BD,连接AC,EC,已知AB=5,DE=1,BD=8,设CD=x.
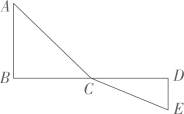 (1)、用含x 的代数式表示AC+CE 的长.(2)、请问:点C 满足什么条件时,AC+CE 的值最小?(3)、根据(2)中的规律和结论,请构图求出代数式 的最小值.17. 我们知道,四边形内角和为360°,若某个四边形有一组对角互补,则另一组对角也必然互补,因此,我们把有一组对角满足互补关系的四边形称为“双补四边形”,例如:在四边形PQRS中,若∠P+∠R=180°(或∠Q+∠S=180°),则称四边形PQRS为“双补四边形”.
(1)、用含x 的代数式表示AC+CE 的长.(2)、请问:点C 满足什么条件时,AC+CE 的值最小?(3)、根据(2)中的规律和结论,请构图求出代数式 的最小值.17. 我们知道,四边形内角和为360°,若某个四边形有一组对角互补,则另一组对角也必然互补,因此,我们把有一组对角满足互补关系的四边形称为“双补四边形”,例如:在四边形PQRS中,若∠P+∠R=180°(或∠Q+∠S=180°),则称四边形PQRS为“双补四边形”. (1)、已知四边形EFGH是“双补四边形”.
(1)、已知四边形EFGH是“双补四边形”.①若∠E:∠F:∠G=7:4:2,则∠H=;
②如图1,若∠F=90°,FG=8,GH= , EH= , 则EF=;
(2)、如图2,在四边形EFGH中,FH平分∠EFG,EH=GH.求证:四边形EFGH是“双补四边形”;(3)、如图3,四边形EFGH是“双补四边形”,EF=FG,点M,N分别在边EH,GH上,且满足EM+GN=MN.试探究∠MFN和∠H之间满足的数量关系,并证明你的结论.18. 实验探究:实验情景示意图

实验使用装置
①一根不可伸缩的绳子绕过定滑轮A,一端固定在滑块B上,另一端固定在物体C上;(、B、C可以视作三个点)
②滑块B可在水平直轨道上左右滑动,以调节物体C的高度.
初始状态
图1物体C静止在轨道上,其到滑轮A的垂直距离为 , 且 .
实验条件
绳子始终绷紧,滑轮、滑块及物体的大小均可忽略.
任务
(1)求绳子的总长度;
(2)图2若物体C升高 , 求滑块B向左滑动的距离.
19. 综合与实践【问题情境】数学活动课上,老师让同学们以“三角形平移与旋转”为主题开展数学活动,和是两个等边三角形纸片,其中, , .

【解决问题】
(1)、勤奋小组将和按图1所示的方式摆放(点A , C , B在同一条直线上),连接AE , BD , 请直接写出AE、BD之间的数量关系.(2)、如图2,创新小组在勤奋小组的基础上继续探究,将绕着点C逆时针方向旋转,当点E恰好落在CD边上时,求的面积.(3)、【拓展延伸】如图3,缜密小组在创新小组的基础上,提出一个问题:“将沿CD方向平移acm得到 . 连接AB' , B'C , 当恰好是以AB'为斜边的直角三角形时,请你求出a的值及AB'长度.
20. 如图,在四边形中, , 相交于点为边上一点,且 . (1)、求证:;(2)、求的度数(用含的代数式表示);(3)、若 , , 求的长.21. 在数学学习中,观察实验猜想证明是研究几何图形性质的一般思路.某班同学运用这个思路对三角形三边平方的关系展开了研究:
(1)、求证:;(2)、求的度数(用含的代数式表示);(3)、若 , , 求的长.21. 在数学学习中,观察实验猜想证明是研究几何图形性质的一般思路.某班同学运用这个思路对三角形三边平方的关系展开了研究:【观察】在直角三角形中,两条直角边长的平方和等于斜边长的平方(设直角边长分别为 , 斜边为 , 那么 . 对于一般的三角形 , 三边长分别为 , 且 , 其边长的平方是否也存在某种关系.
【实验操作】小组成员通过测量不同类型三角形(锐角三角形,钝角三角形)三边的长度,计算它们的平方并进行比较,猜想三边平方之间的关系:
当是锐角三角形时,三边之间的关系是:;
当是钝角三角形时,三边之间的关系是: ① .
【证明思路】为了将锐角三角形与我们熟悉的直角三角形联系起来,过点作 , 垂足为 . 这样就把锐角分成了两个直角三角形和 , 从而可以运用勾股定理进行边的关系推导.
以下是小组成员的证明过程:
如图①,过点作 , 垂足为 . 设 .
在中, ,
在中, ② , ② .
化简得, .
.
.
.

(1)其中,①是_______;②是_______.
【知识迁移】(2)如图②,当是钝角三角形时,请证明与之间的关系.
22. 轴对称变换是现实世界运动变化的三种常见形式之一,在数学活动课上,同学们研究利用轴对称变化探究图形中线段的数量关系.【初步感知】
(1)如图1,四边形中, , 平分 , 求证: .
①如图2,小明同学想到了翻折 , 给出如下解题思路:在上截取 , 连接;
②如图3,小丽同学想到了翻折 , 给出了如下解题思路:延长线段到点 , 使 , 连接;
请你选择一名同学的解题思路,写出证明过程;

【深入探究】
(2)如图4,中, , 平面内有点(点和点在的同侧),连接 , , , . 求证:;

【拓展延伸】
(3)如图5,在(2)的条件下,若平分 , , 请求出线段的长度.
 23. 如图,在 , , , 是上一动点,以为底,在的右侧作等腰直角 , 的延长线交于点 .
23. 如图,在 , , , 是上一动点,以为底,在的右侧作等腰直角 , 的延长线交于点 .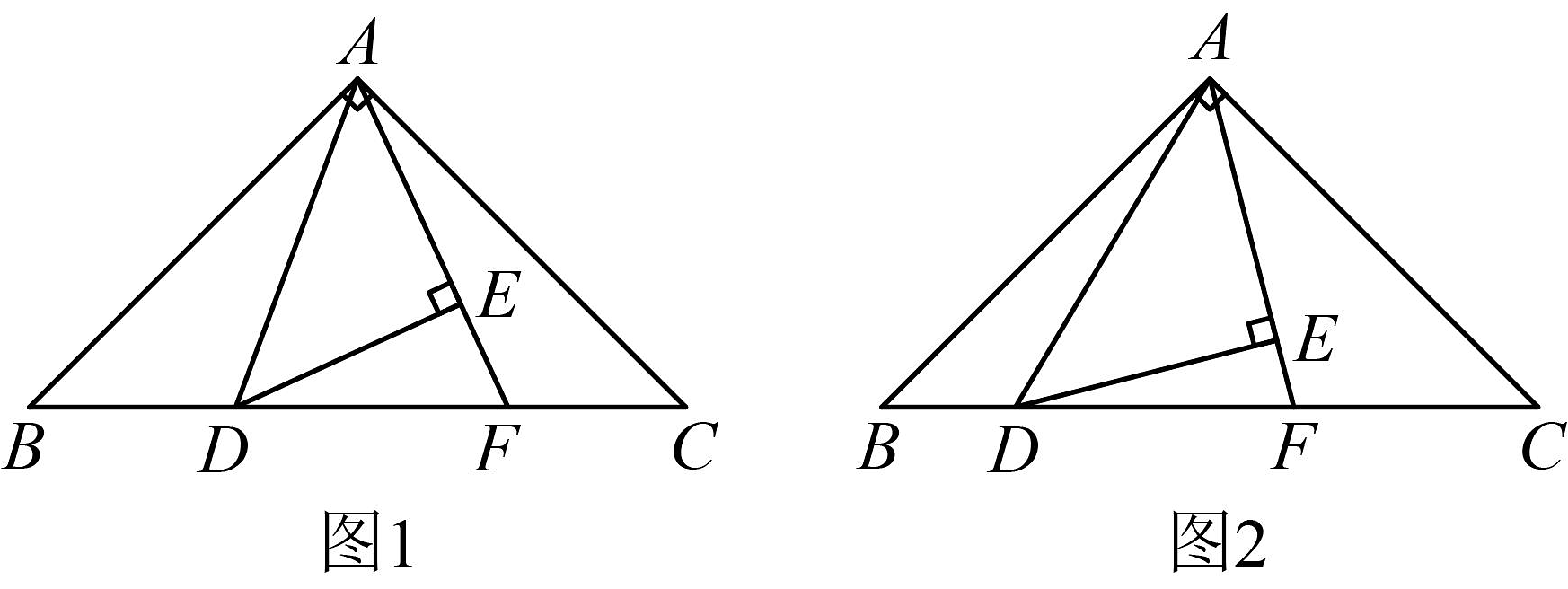 (1)、如图1;当时,
(1)、如图1;当时,①求证:;
②若 , 求线段的长;
(2)、如图2,若 , , 求线段的长;