冀教版七(下)数学 第七章 相交线与平行线 单元测试提升卷
试卷更新日期:2026-01-04 类型:单元试卷
一、选择题(本大题共12小题,每小题3分,共36分))
-
1. 宇树机器人“G1”如图所示,将它通过平移可得到的图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 如图,在观测站发现客轮、货轮分别在它北偏西、西南方向,则的度数是( )
2. 如图,在观测站发现客轮、货轮分别在它北偏西、西南方向,则的度数是( ) A、 B、 C、 D、3. 如图,在所标注的角中,可以看成是一对内错角的是( )
A、 B、 C、 D、3. 如图,在所标注的角中,可以看成是一对内错角的是( ) A、∠1和∠2 B、∠2和∠3 C、∠1和∠3 D、∠2 和∠44. 如图,已知a//b,直角三角板的直角顶点在直线b上,若∠1=52°,则下列结论正确的是( )
A、∠1和∠2 B、∠2和∠3 C、∠1和∠3 D、∠2 和∠44. 如图,已知a//b,直角三角板的直角顶点在直线b上,若∠1=52°,则下列结论正确的是( ) A、∠3=48° B、∠4=132° C、∠5=48° D、∠2=52°5. 如图,B点在处的南偏西方向,处在处的南偏东方向,处在北偏东方向,则( )
A、∠3=48° B、∠4=132° C、∠5=48° D、∠2=52°5. 如图,B点在处的南偏西方向,处在处的南偏东方向,处在北偏东方向,则( ) A、 B、 C、 D、6. 如图,直线l∥AB,∠A=2∠B.若∠1=108°,则∠2的度数为( )
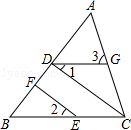
A、 B、 C、 D、6. 如图,直线l∥AB,∠A=2∠B.若∠1=108°,则∠2的度数为( ) A、36° B、46° C、72° D、82°7. 如图, , 分别交于点 , 链接 , 点G是线段CD上的点,连接FG,若 , , 则结论① , ② , ③ , 正确的是( )
A、36° B、46° C、72° D、82°7. 如图, , 分别交于点 , 链接 , 点G是线段CD上的点,连接FG,若 , , 则结论① , ② , ③ , 正确的是( ) A、①② B、②③ C、①③ D、①②③8. 如图,探照灯、锅形天线、汽车灯以及其他很多灯具都与抛物线形状有关,如图所示是一探照灯灯碗的纵剖面,从位于O点的灯泡发出的两束光线OB,OC经灯碗反射以后平行射出.如果图中∠ABO=α,∠DCO=β,则∠BOC的度数为( )
A、①② B、②③ C、①③ D、①②③8. 如图,探照灯、锅形天线、汽车灯以及其他很多灯具都与抛物线形状有关,如图所示是一探照灯灯碗的纵剖面,从位于O点的灯泡发出的两束光线OB,OC经灯碗反射以后平行射出.如果图中∠ABO=α,∠DCO=β,则∠BOC的度数为( ) A、180°-α-β B、α+β C、(α+β) D、90°+(β-α)9. 如图,则与的数量关系是( )
A、180°-α-β B、α+β C、(α+β) D、90°+(β-α)9. 如图,则与的数量关系是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共4小题,每小题3分,共12分)
-
10. 如图,AB∥CD,BC∥ED,∠B=80°,则∠D=.
 11. 图1是一款充电夹子式折叠台灯,图2为其平面示意图,该台灯放在水平的桌面MN上,AB,BC,CD为支架连杆,DE为台灯灯面,它们可绕连接点B,C,D旋转,已知 , 台灯长 , 在旋转接点B,C,D的过程中,点B,E之间的最大距离是cm.若 , 则度.
11. 图1是一款充电夹子式折叠台灯,图2为其平面示意图,该台灯放在水平的桌面MN上,AB,BC,CD为支架连杆,DE为台灯灯面,它们可绕连接点B,C,D旋转,已知 , 台灯长 , 在旋转接点B,C,D的过程中,点B,E之间的最大距离是cm.若 , 则度. 12. 已知直线 , 点、分别在、上,如图所示,射线按顺时针方向以每秒的速度旋转至便立即回转,并不断往返旋转;射线按顺时针方向每秒旋转至停止.此时射线也停止旋转,若射线先转秒,射线才开始转动,当射线旋转的时间为秒时, .
12. 已知直线 , 点、分别在、上,如图所示,射线按顺时针方向以每秒的速度旋转至便立即回转,并不断往返旋转;射线按顺时针方向每秒旋转至停止.此时射线也停止旋转,若射线先转秒,射线才开始转动,当射线旋转的时间为秒时, .
三、解答题(本大题共8小题,共72分)
-
13. 如图,在的方格中,每个小正方形边长均为1个单位长度.的顶点、点和点都在格点上.仅用无刻度直尺作图,保留作图痕迹,不写作法.
 (1)、过点作的垂线段;(2)、过点作的平行线.14. “苍南1号”是我国第一个平价海上风电项目,服务于国家“双碳”战略,具有显著的环境效益和经济效益.如图1所示,风电机的塔架垂直于海平面,叶片 , , 可绕着轴心旋转,且 .
(1)、过点作的垂线段;(2)、过点作的平行线.14. “苍南1号”是我国第一个平价海上风电项目,服务于国家“双碳”战略,具有显著的环境效益和经济效益.如图1所示,风电机的塔架垂直于海平面,叶片 , , 可绕着轴心旋转,且 . (1)、如图2,当时,求的度数.(2)、叶片从图3位置(与重合)开始绕点顺时针旋转,若旋转后与互补,则旋转的最小角度是多少度?15. 如图,已知GF⊥AB,CD⊥AB,∠CDE和∠CGF互补.
(1)、如图2,当时,求的度数.(2)、叶片从图3位置(与重合)开始绕点顺时针旋转,若旋转后与互补,则旋转的最小角度是多少度?15. 如图,已知GF⊥AB,CD⊥AB,∠CDE和∠CGF互补. (1)、判断 DE与 BC是否平行,并说明理由;(2)、若∠CDE=36°,求∠B的度数.16. 如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°.
(1)、判断 DE与 BC是否平行,并说明理由;(2)、若∠CDE=36°,求∠B的度数.16. 如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°. (1)、求证:EF∥AB;(2)、若∠CEF=70°,求∠ACB的度数.17. 综合与实践.
(1)、求证:EF∥AB;(2)、若∠CEF=70°,求∠ACB的度数.17. 综合与实践.主题:探究平行线的性质与判定.素材:一副三角尺(一块含 , 一块含)、两根相同的长木棒.
步骤1:如图,摆放两根木棒使(可上下平移调节距离).

步骤2:将一副三角尺按如图方式进行摆放,恰好满足 , .
(1)、的度数为 , 的度数为 ;(2)、试判断与的位置关系,并说明理由.