冀教版七（下）数学第七章相交线与平行线单元测试基础卷

试卷更新日期：2026-01-04 类型：单元试卷

进入出卷网下载

一、选择题(本大题共12小题，每小题3分，共36分)

1. 对于命题“若a²＞b² ，则a＞b”，下面四组关于a ， b的值中，能说明这个命题是假命题的是（　　）

A、a=3，b=2 B、a=－3，b=2 C、a=3，b=－1 D、a=－1，b=3

查看试题解析
2. 如图，下列说法中，错误的是（）

A、∠1与∠2是同位角 B、∠2与∠3是同位角 C、∠1与∠4是内错角 D、∠2与∠4是同旁内角

查看试题解析
3. 如图，已知 $A B ∥ E D$ ， $∠ E C F = 65 °$ ，则 $∠ B A C$ 的度数为（）

A、 $115 °$ B、 $60 °$ C、 $65 °$ D、 $75 °$

查看试题解析
4. 在跳远比赛中，某同学从点C处起跳后，在沙池留下的脚印如图所示，测量线段 $A B$ 的长度作为他此次跳远成绩（最近着地点到起跳线的最短距离），依据的数学原理是（）

A、垂线段最短 B、两点确定一条直线 C、两点之间，线段最短 D、两直线平行，内错角相等

查看试题解析
5. 如图，将三角形ABC沿BC方向平移得到三角形DEF，若BF=7，EC=1，则平移的距离是（）

A、3 B、4 C、6 D、8

查看试题解析
6. 下列窗棂图案中，可以看作由一个“基本图案”经过平移得到的是（）

A、
四钱纹样式 B、
梅花纹样式 C、
拟日纹样式 D、
海棠纹样式

查看试题解析
7. 如图，某条行车路线共拐了三次弯，最后行车路线与开始的路线是平行的．已知第一次转过的角度为120°，第三次转过的角度为135°，则第二次转过的角度为（ )

A、75° B、60° C、135° D、120°

查看试题解析
8. 如图所示，某住宅小区内有一长方形地块，想在长方形地块内修筑同样宽的两条“之”字形路，余下部分绿化，道路的宽为 $2 m$ ，则绿化的面积为（） $m^{2}$

A、 $564$ B、 $550$ C、 $544$ D、 $540$

查看试题解析
9. 如图，正五边形 $A B C D E$ 的顶点 $B$ 、 $D$ 分别在一把直尺的两边上 $($ 直尺为长方形 $)$ ，若 $∠ 1 = 50 °$ ，则图中 $∠ 2$ 的度数为( )

A、 $20 °$ B、 $22 °$ C、 $25 °$ D、 $30 °$

查看试题解析
10. 如图，AB//CD，点E是CD上一点，点F是AB上一点，∠AEC与∠FED互余，已知∠AFE=39°，则∠AEC的度数是（）

A、51° B、61° C、39° D、141°

查看试题解析
11. 生活中常见一种折叠拦道闸如图1所示．若想求解某些特殊状态下的角度，需将其抽象为如图2所示的几何图形，其中 $B A ⊥ A E$ ，垂足为A， $C D ∥ A E$ ，则 $∠ A B C + ∠ B C D =$ （）

A、 $270 °$ B、 $250 °$ C、 $230 °$ D、 $200 °$

查看试题解析
12. 如图，四边形ABCD中，BD与AC相交于点O，AE∥CF，E，F在BD上，下列条件中能推出AB∥CD的是 ( )

A、∠1=∠2 B、∠3=∠4 C、∠DAE=∠BCF D、∠BAD=∠DCB

查看试题解析

二、填空题(本大题共4小题，每小题3分，共12分)

13. 判断命题“如果 $n < 2$ ，那么 $n^{2} - 4 < 0$ ”是假命题，举出一个反例，反例中的 $n$ 可以为．

查看试题解析
14. 已知直线 A D 与 B E 交于点 $O, ∠ D O E = 2 8^{°}, ∠ B O F = 7 0^{°}$ ，则 $∠ A O F =$ °。

查看试题解析
15. 如图，∠1=140°，∠2=40°，∠3=108°，则∠4=时，AB∥EF.

查看试题解析

三、解答题(本解答题(本大题共8小题，共72分)

16. 如图，由若干个小正方形构成的网格中有一个 $△ A B C$ ， $△ A B C$ 的三个顶点都在格点上，按要求进行下列作图：（只借助于网格，需写出结论）

(1)、过点B画出 $A C$ 的平行线 $B D$ ；

(2)、画出先将 $△ A B C$ 向右平移2格，再向上平移3格后的 $△ A^{'} B^{'} C^{'}$ ．

查看试题解析
17. 下列各语句中，哪些是命题，哪些不是命题？是命题的，请先将它改写为“如果……那么……”的形式，再指出命题的条件和结论.

(1)、同号两数的和一定不是负数；

(2)、若x＝2，则10－5x＝0；

(3)、在直线AB上任取一点P.

查看试题解析
18. 如图，已知∠1+∠2=180°，且∠3=∠B．

(1)、试判断EF和BC的位置关系，并说明理由；

(2)、若CE平分∠ACB，且∠2=108°，∠3=52°，求∠AFE的度数．

查看试题解析
19. 如图，已知 $B C / / D F, ∠ B = ∠ D, A, F, B$ 三点共线，连结AC交DF于点 $E$ ．

(1)、试说明 $∠ A = ∠ A C D$ ．

(2)、若 $F G / / A C, ∠ A + ∠ B = 11 0^{°}$ ，求 $∠ E F G$ 的度数．

查看试题解析
20. 现有一块含 $30 °$ 角的直角三角尺 $A O B$ ， $∠ A O B$ 是直角，其顶点 $O$ 在直线 $l$ 上，请解决下列问题：

(1)、如图1，请直接写出 $∠ 1$ 、 $∠ 2$ 的数量关系；

(2)、如图2，分别过点 $A$ 、 $B$ 作直线 $l$ 的垂线，垂足分别为 $C$ 、 $D$ ，请写出图中分别与 $∠ 1$ 、 $∠ 2$ 相等的角，并说明理由；

(3)、如图3， $A C$ 平分 $∠ O A B$ ，将直角三角尺 $A O B$ 绕着点 $O$ 旋转，当 $A C ∥ l$ 时，请直接写出 $O B$ 与直线 $l$ 所成锐角的度数．

查看试题解析
21. 如图①，把一块含 $30 °$ 角的直角三角尺 $A B C$ 的 $B C$ 边放置于长方形直尺 $D E F G$ 的 $E F$ 边上．

(1)、填空： $∠ 1 =$ ______°， $∠ 2 =$ ______°；

(2)、现把三角尺绕点 $B$ 逆时针旋转 $n$ ．
①如图②．当 $0 ° < n < 90 °$ ，且点 $C$ 恰好落在 $D G$ 边上时，求 $∠ 1$ ， $∠ 2$ 的度数（结果用含 $n$ 的式子表示）；
②当 $0 ° < n < 180 °$ 时，是否会存在三角尺某一边所在的直线与直尺（有四条边）某一边所在的直线垂直？如果存在，请直接写出所有 $n$ 的值和对应的那两条垂线；如果不存在，请说明理由．

查看试题解析
22. 实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等．如图1，一束光线 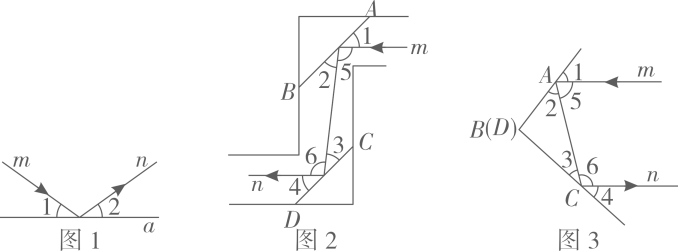$m$ 射到平面镜 $a$ 上，被 $a$ 反射后的光线为 $n$ ，则入射光线 $m$ 、反射光线 $n$ 与平面镜 $a$ 所夹的锐角 $∠ 1 = ∠ 2$ ．

(1)、利用这个规律人们制作了潜望镜，图2是潜望镜的工作原理示意图，AB、CD是平行放置的两面平面镜．已知光线经过平面镜反射时，有 $∠ 1 = ∠ 2, ∠ 3 = ∠ 4$ ，请判断入射光线 $m$ 和反射光钱 $π$ 是否平行，并说明理由．

(2)、显然，改变两面平面镜AB、CD之间的位置关系、经过两次反射后，入射光线 $m$ 与反射光线 $n$ 之间的位置关系会随之改变，如图3，一束光线 $m$ 射到平面镜AB上，被AB反射到平面镜CD上，又被CD反射．若被CD反射出的光线 $n$ 和光线 $m$ 平行，且 $∠ 1 = 4 7^{°}$ ，则 $∠ 6 =$ °， $∠ A B C =$ °．

(3)、试猜想：在图3中，当两平面镜AB，CD的夹角 $∠ A B C$ 的度数是多少时，可以使任何入射光线 $m$ 经过平面镜AB、CD的两次反射后，与反射光线 $n$ 平行？请说明理由．

查看试题解析

冀教版七（下）数学 第七章 相交线与平行线 单元测试基础卷

一、选择题(本大题共12小题，每小题3分，共36分)

二、填空题(本大题共4小题，每小题3分，共12分)

三、解答题(本解答题(本大题共8小题，共72分)

冀教版七（下）数学第七章相交线与平行线单元测试基础卷