《旋转》精选典型题——人教版九年级上学期数学期末复习

试卷更新日期：2025-12-30 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图，P为等边 $△ A B C$ 内一点，且 $P B = 6 ， P C = 8 ， ∠ B P C = 150 °$ ， M、N为边 $A B 、 A C$ 上的动点，且 $A M = A N$ ，则 $P M + P N$ 的最小值为（）

A、10 B、8 C、6 D、4

查看试题解析
2. 如图所示， $A_{1} (1, \sqrt{3})$ ， $A_{2} (\frac{3}{2}, \frac{\sqrt{3}}{2})$ ， $A_{3} (2, \sqrt{3})$ ， $A_{4} (3, 0)$ ．将折线 $O A_{1} A_{2} A_{3} A_{4}$ 绕点 $A_{4}$ 顺时针旋转 $180^{\circ}$ 得出新的折线，再将新的折线绕点 $A_{8}$ 顺时针旋转 $180^{\circ}$ ……以此类推，得到一个大的折线．现有一动点 $P$ 从原点 $O$ 出发，沿着折线以每秒1个单位的速度移动，设运动时间为 $t$ ．当 $t = 2024$ 时，点 $P$ 的坐标为（　　）

A、 $(1012, - \sqrt{3})$ B、 $(1012.5, - \frac{\sqrt{3}}{3})$ C、 $(1013, - \sqrt{3})$ D、 $(1014, 0)$

查看试题解析
3. 如图，矩形 $A B C D$ 中，顶点 $A (0, 4)$ ， $B (- 2, 0)$ ， $C (- 4, 1)$ ，将矩形 $A B C D$ 绕点O逆时针旋转，每秒旋转 $45 °$ ，则第100秒旋转结束时，点D的坐标为( )

A、 $(- 2, 5)$ B、 $(2, - 5)$ C、 $(1, - 6)$ D、 $(- 2, - 5)$

查看试题解析

二、填空题

4. 如图，在四边形ABCD中， $A D / / B C$ ，点E在在四边形ABCD的内部，且 $D E = E C$ ， $∠ D E C = ∠ A E B = 12 0^{°}$ ，已知 $A D = 4, B C = 6$ ，则AB的长为.

查看试题解析
5. 如图，在正方形 $A B C D$ 中， $A D = 2 \sqrt{3}$ ，把边 $B C$ 绕点B逆时针旋转 $30 °$ 得到线段 $B P$ ，连接 $A P$ 并延长交 $C D$ 于点E，则线段 $P E$ 的长为．

查看试题解析
6. 如图，正方形ABCD中，AB=5cm，以B为圆心，2cm长为半径画⊙B，点P在⊙B上移动，连接AP，并将AP绕点A逆时针旋转90°至AP^' ，连接BP^' ．在点P移动的过程中，BP^'长度的最小值为cm．

查看试题解析
7. 如图，四边形 $A B C D$ 和四边形 $A E F G$ 均为正方形，点 $D$ 为 $E F$ 的中点，若 $A B = \sqrt{5}$ ，连接 $B F$ ，则 $B F$ 的长为．

查看试题解析
8. 如图，将矩形 $A B C D$ 绕点A旋转至矩形 $A B^{^{'}} C^{^{'}} D^{^{'}}$ 位置，此时 $A C^{'}$ 的中点恰好与D点重合， $A B^{'}$ 交 $C D$ 于点 $E .$ 若 $A B = 3$ ，则 $△ A E C$ 的面积为．

查看试题解析
9. 如图，把正方形铁片OABC置于平面直角坐标系中，顶点A的坐标为（3，0），点P（1，2）在正方形铁片上，将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°，第一次旋转至图①位置，第二次旋转至图②位置···，则正方形铁片连续旋转2017次后，点P的坐标为．

查看试题解析

三、解答题

10. 四边形 $A B C D$ 是菱形， $∠ A = 45 °$ ，点 $E$ 是 $A B$ 边上一点，连接 $D E, C E$ ．

(1)、如图1，若菱形边长为4，当 $D E ⊥ A B$ 时，求线段 $C E$ 的长；

(2)、线段 $D E$ 绕点 $D$ 逆时针旋转 $45 °$ 得到线段 $D F$ ，如图2，连接 $A F$ ，点 $G$ 是 $A F$ 中点，连接 $D G$ ．求证： $C E = 2 D G$ ；

(3)、如图3，将线段 $D E$ 绕点 $D$ 逆时针旋转 $90 °$ 得到线段 $D F$ ，连接 $C F$ ，点 $E$ 在射线 $A B$ 上运动的过程中，当 $C F$ 取最小值时，直接写出 $\frac{S_{△ B E C}}{S_{△ A D E}}$ 的值．

查看试题解析
11. 定义：如果两个正方形满足，一个正方形的边长与另一个正方形的对角线长相等，那么称这两个正方形互为“完美嵌套”

(1)、若两个互为“完美嵌套”正方形的边长分别为a，b，则a，b满足的关系式为；

(2)、如图1，正方形ABCD和正方形AEFG互为“完美嵌套”，边AE在边AB上，且AB=12.将正方形AEFG绕点A逆时针旋转α(0°≤α≤45°)
①在旋转的过程中，当∠BEA=120°时，试求BE的长；
②BE的延长线交直线DG于点Q，当正方形AEFG由图1绕点A逆时针旋转45°，请求出在旋转过程中四边形BDQA面积的最大值.

查看试题解析
12. 【问题情景】1643年，法国数学家费马曾提出一个著名的几何问题：给定不在同一条直线上的三个点A，B，C，求平面上到这三个点的距离之和最小的点的位置，意大利数学家和物理学家托里拆利给出了分析和证明，该点也被称为“费马点”或“托里拆利点”，该问题也被称为“将军巡营”问题．
【理解运用】
（1）下面是该问题的一种常见的解决方法，请补充以下推理过程：
当 $△ A B C$ 的三个内角均小于 $120 °$ 时，如图1，将 $△ A P C$ 绕点 $C$ 顺时针旋转 $60 °$ 得到 $△ A^{'} P^{'} C$ ，连接 $P P^{'}$ ，由 $P C = P^{'} C ， ∠ P C P^{'} = 60 °$ ，可知 $△ P C P^{'}$ 为_______（选“直角”或“等边”）三角形，故 $P P^{'} = P C$ ，又 $P^{'} A^{'} = P A$ ，故 $P A + P B + P C = P^{'} A^{'} + P B + P P^{'} \geq A^{'} B$ ，由_______（选“两点之间线段最短”或“三角形两边之和大于第三边”）可知，当 $B ， P ， P^{'} ， A^{'}$ 在同一条直线上时， $P A + P B + P C$ 取最小值，如图2，最小值为 $A^{'} B$ ，此时的 $P$ 点为该三角形的“费马点”，且有 $∠ A P C = ∠ B P C = ∠ A P B =$ _______（填写角度数）；已知当 $△ A B C$ 有一个内角大于或等于 $120 °$ 时，“费马点”为该三角形的某个顶点．如图3，若 $B A C \geq 120 °$ ，则该三角形的“费马点”为_______（选“A”或“B”或“C”）点；
【深入探究】
（2）如图4，在 $△ A B C$ 中，三个内角均小于 $120 °$ ，且 $A C = 3 ， B C = 4 ， ∠ A C B = 30 °$ ，已知点 $P$ 为 $△ A B C$ 的“费马点”，求 $P A + P B + P C$ 的值．

查看试题解析
13. 在数学综合与实践活动课上，同学们用两个完全相同的矩形纸片展开探究活动：
【实践探究】：（1）小红将两个矩形纸片摆成图1的形状，连接 $A G 、 A C$ ，则 $∠ A C G =$ __________ $°;$
【解决问题】：（2）将矩形 $A Q G F$ 绕点A顺时针转动，边 $A F$ 与边 $C D$ 交于点M，连接 $B M$ ， $A B = 10, A D = 6$ ．
①如图2，当 $B M = A B$ 时，求证： $A M$ 平分 $∠ D M B$ ，写出证明过程；
②如图3，当点F落在 $D C$ 上时，连接 $B Q$ 交 $A F$ 于点O，则 $A O =$ __________；
【迁移应用】：（3）如图4，正方形 $A B C D$ 的边长为 $5 \sqrt{2}, E$ 是 $B C$ 边上一点（不与点 $B 、 C$ 重合），连接 $A E$ ，将线段 $A E$ 绕点E顺时针旋转 $90 °$ 至 $F E$ ，作射线 $F C$ 交 $A B$ 的延长线于点G，则 $B G =$ __________；
（4）如图5，在菱形 $A B C D$ 中， $∠ A = 120^{°}, E$ 是 $C D$ 边上一点（不与点 $C 、 D$ 重合），连接 $B E$ ，将线段 $B E$ 绕点E顺时针旋转 $120 °$ 至 $F E$ ，作射线 $F D$ 交 $B C$ 的延长线于点G，若 $B G = 6 \sqrt{3}$ ，求 $C G$ 的长并说明理由．

查看试题解析
14. 矩形ABCD中， $C B = 6, A B = 8$ ，矩形ABCD绕点 $A$ 逆时针旋转得到矩形 $A B^{^{'}} C^{^{'}} D^{^{'}} (B$ 与 $B^{^{'}}$ 对应， $C$ 与 $C^{^{'}}$ 对应)，连接 $C C^{^{'}} 、 B B^{^{'}}$ 交于点 $M$ .

(1)、如图1，当 $D^{^{'}}$ 落在边AB上时， $B B^{^{'}}$ 与 $C^{^{'}} D^{^{'}}$ 交于点 $N$ ，求证： $M C = M C^{^{'}}$

(2)、当矩形 $A B^{^{'}} C^{^{'}} D^{^{'}}$ 旋转到如图2时，若点 $E$ 为AC的中点，连接ME，求ME的长；

(3)、将矩形ABCD绕点A逆时针旋转一周的过程中，当 $∠ A C C^{^{'}} = 6 0^{°}$ 时，则 $B^{^{'}} M$ 的长为.

查看试题解析
15. 小明在一次数学活动中，进行了如下的探究活动：如图，在矩形 $A B C D$ 中， $A B = 5$ ， $A D = 3$ ，以点 $B$ 为中心，顺时针旋转矩形 $A B C D$ ，得到矩形 $B G F E$ ，点 $A$ 、 $D$ 、 $C$ 的对应点分别为 $G$ 、 $F$ 、 $E$ ．

(1)、如图①，当点 $G$ 落在 $C D$ 边上时，求 $D G$ 的长；

(2)、如图②，当点 $G$ 落在线段 $D F$ 上时， $B G$ 与 $C D$ 交于点 $H$ ．求 $D H$ 的长．

(3)、记点 $K$ 为矩形 $A B C D$ 对角线的交点，连接 $K G$ 、 $K F$ ，记 $△ K G F$ 面积为 $S$ ，求 $S$ 的取值范围．

查看试题解析
16. 阅读下面材料，并解决问题：

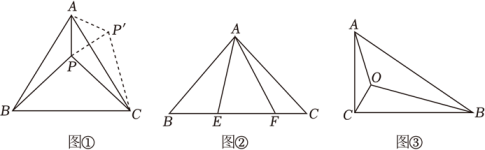(1)、如图①等边 $Δ A B C$ 内有一点 $P$ ，若点 $P$ 到顶点 $A$ ， $B$ ， $C$ 的距离分别为3，4，5，求 $∠ A P B$ 的度数．
为了解决本题，我们可以将 $Δ A B P$ 绕顶点 $A$ 旋转到 $Δ A C P^{'}$ 处，此时 $Δ A C P^{'} ≅ Δ A B P$ ，这样就可以利用旋转变换，将三条线段 $P A$ ， $P B$ ， $P C$ 转化到一个三角形中，从而求出 $∠ A P B =$ ；

(2)、基本运用
请你利用第（1）题的解答思想方法，解答下面问题
已知如图②， $Δ A B C$ 中， $∠ C A B = 90 °$ ， $A B = A C$ ， $E$ ， $F$ 为 $B C$ 上的点且 $∠ E A F = 45 °$ ，求证： $E F^{2} = B E^{2} + F C^{2}$ ；

(3)、能力提升
如图③，在 $R t Δ A B C$ 中， $∠ C = 90 °$ ， $A C = 1$ ， $∠ A B C = 30 °$ ，点 $O$ 为 $R t Δ A B C$ 内一点，连接 $A O$ ， $B O$ ， $C O$ ，且 $∠ A O C = ∠ C O B = ∠ B O A = 120 °$ ，求 $O A + O B + O C$ 的值．

查看试题解析
17. 【阅读理解】
半角模型是指有公共顶点，锐角等于较大角的一半，且组成这个较大角的两边相等．通过旋转或截长补短，将角的倍分关系转化为角的相等关系，并进一步构成全等三角形，用以解决线段关系、角度、面积等问题，
【初步探究】
如图1，在正方形 $A B C D$ 中，点 $E, F$ 分别在边 $B C, C D$ 上，连接 $A E, A F, E F$ ．若 $∠ E A F = 45 °$ ，将 $△ A D F$ 绕点 $A$ 顺时针旋转 $90 °$ ，点 $D$ 与点 $B$ 重合，得到 $△ A B G$ ．易证： $△ A E F ≌ △ A E G$ ．
（1）根据以上信息，填空：
① $∠ E A G =$ _______°；
②线段 $B E 、 E F 、 D F$ 之间满足的数量关系为_______；
【迁移探究】
（2）如图2，在正方形 $A B C D$ 中，若点 $E$ 在射线 $C B$ 上，点 $F$ 在射线 $D C$ 上， $∠ E A F = 45 °$ ，猜想线段 $B E 、 E F 、 D F$ 之间的数量关系，请证明你的结论；
【拓展探索】
（3）如图3，已知正方形 $A B C D$ 的边长为 $3 \sqrt{2}, ∠ E A F = 45 °$ ，连接 $B D$ 分别交 $A E 、 A F$ 于点 $M 、 N$ ，若点 $M$ 恰好为线段 $B D$ 的三等分点，且 $B M < D M$ ，求线段 $M N$ 的长．

查看试题解析
18. 如图，正方形 $A B C D$ 中，点E在边 $A D$ 上（不与端点A，D重合），点A关于直线 $B E$ 的对称点为点F，连接 $C F$ ，设 $∠ A B E = α$ ．

(1)、求 $∠ B C F$ 的大小（用含 $α$ 的式子表示）；

(2)、将 $△ A B E$ 绕点B顺时针旋转 $90 °$ 得到 $△ C B H$ ，点E的对应点为点H，画出旋转后的 $△ C B H$ ；

(3)、在（2）的条件下连接 $B F$ ， $H F$ ．当E为 $A D$ 的中点时，判断 $△ B F H$ 的形状，并说明理由．

查看试题解析
19. 综合与实践
【主题】折纸问题探究
【素材】
①一张三角形纸片（如图①）；
②一张矩形纸片（如图③）．
【实践操作】
步骤1：如图①，将三角形纸片 $A B C (A B > A C)$ 沿过点A的直线折叠，使得 $A C$ 落在 $A B$ 边上，折痕为 $A D$ ，展开纸片；
步骤2：如图②，在第一次的折叠基础上第二次折叠该三角形纸片，使点A和点D重合，折痕为 $E F$ ，展平纸片后得到 $△ A E F$ ．
步骤3：如图③，将矩形纸片 $A B C D$ 沿过点B的直线折叠，使点A落在 $B C$ 边上的点F处，折痕为 $B E$ ；
步骤4：如图④，再沿过点E的直线折叠，使点D落在 $B E$ 上的点 $D^{'}$ 处，折痕为 $E G$ ；
步骤5：如图⑤，再展平纸片．
【实践探索】

(1)、观察与发现：在图②中，试判断 $△ A E F$ 的形状，并说明理由．

(2)、实践与计算：在图⑤中，求 $∠ α$ 的大小．

查看试题解析
20. 在等边 $△ A B C$ 中，

(1)、如图1，D为 $△ A B C$ 外一点， $∠ B D C = 120 °$ ．求证； $A D = D B + D C$ ；

(2)、如图2，D为 $A B$ 边上一动点，连 $C D$ ，将 $C D$ 绕着D逆时针旋转 $120 °$ 得到 $D E$ ，连 $B E$ ，取 $B E$ 中点 F，连 $D F$ ，猜想 $A D$ 与 $D F$ 的数量关系，并证明你的猜想；

(3)、如图3， $∠ P O Q = 60 °$ ，过C作 $C D ⊥ O P$ 于D，作 $C E ⊥ O Q$ 于E， $(O D > O A, O E > O B)$ ，若 $A D = n B E$ ，求 $\frac{O A}{O B}$ 的值．（用含n的代数式表示）

查看试题解析
21. 如图1，在 $Rt △ A B C$ 中， $∠ A = 90 °$ ， $A B = A C$ ，点 $D$ 、 $E$ 分别在边 $A B$ 、 $A C$ 上， $A D = A E$ ，连接 $D C$ ，点 $M$ 、 $P$ 、 $N$ 分别为 $D E$ 、 $D C$ 、 $B C$ 的中点．

(1)、观察猜想：图1中，线段 $P M$ 与 $P N$ 的数量关系是，位置关系是；

(2)、探究证明：把 $△ A D E$ 绕点A逆时针方向旋转到图2的位置，连接 $M N$ ， $B D$ ， $C E$ ，判断 $△ P M N$ 的形状，并说明理由；

(3)、拓展延伸：把 $△ A D E$ 绕点A在平面内自由旋转，若 $A D = 2$ ， $A B = 4$ ，直接写出 $△ P M N$ 面积的最大值．

查看试题解析
22. 已知，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 3$ ， $B C = 4$ ． P是 $B C$ 边上一动点（P不与B、C重合），将 $△ A C P$ 沿 $A P$ 折叠得 $△ A D P$ ，点C的对应点为D ．

(1)、【特例感知】
如图1，当点D落在 $A B$ 上时，求 $C P$ 的长；

(2)、【类比迁移】
如图2，当点D在 $A B$ 上方且满足 $∠ B = 2 ∠ B A D$ 时，求 $C P$ 的长；

(3)、【拓展提升】
如图3，将线段 $A P$ 绕点A逆时针旋转 $90 °$ 得 $A E$ ，连接 $D E$ ．当 $△ A D E$ 为等腰三角形时，直接写出 $C P$ 长；

查看试题解析
23. 如图，已知 $△ A B C$ 为等腰直角三角形， $∠ B A C = 90 °$ ， $A B = A C$ ，点D、E分别为边 $A B$ 、 $B C$ 上的一动点（且满足 $∠ C E D < 90 °$ ），连接 $D E$ ，将线段 $D E$ 绕点D逆时针旋转 $90 °$ 得到线段 $D F$ ，连接 $E F$ 、 $B F$ ．

(1)、如图1，当点D与点A重合时，求证：① $C E = B F$ ；② $∠ C B F = 90 °$ ；

(2)、如图2，当点D与点A不重合时，结论 $∠ C B F = 90 °$ 是否仍然成立？请说明理由：

(3)、如图3，在（2）的条件下，过点D作 $D M ⊥ B F$ ，垂足为M．试探究线段 $B E$ 、 $B F$ 、 $M F$ 之间的数量关系，并证明你的结论．

查看试题解析