2025-2026学年北师大版数学九年级上册期末测试模拟题一[范围:九年级全册]
试卷更新日期:2025-12-27 类型:期末考试
一、选择题(每题3分,共36分)
-
1. 关于x的方程根的情况为( )A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、只有一个实数根2. 已知点(﹣2,y1),(3,y2),(7,y3)都在二次函数y=﹣(x﹣2)2+c的图象上,则y1 , y2 , y3的大小关系是( )A、y1>y2>y3 B、y1>y3>y2 C、y2>y1>y3 D、y3>y2>y13. 如图所示,在矩形中, , 点 , 分别在边 , 上.连接 , 将四边形沿翻折,点 , 分别落在点 , 处.则的值是( )
 A、2 B、 C、 D、4. 如图,为的直径,点B,D在上, , , 则的长为( )
A、2 B、 C、 D、4. 如图,为的直径,点B,D在上, , , 则的长为( ) A、2 B、 C、 D、45. 如图,用四个全等的直角三角形拼成“赵爽弦图”,得到大正方形ABCD和小正方形EFGH,连接BD交CH于点P. 若 , 则的值是( )
A、2 B、 C、 D、45. 如图,用四个全等的直角三角形拼成“赵爽弦图”,得到大正方形ABCD和小正方形EFGH,连接BD交CH于点P. 若 , 则的值是( ) A、 B、 C、 D、6. 如图,在平面直角坐标系中,O为坐标原点,Rt△OBA的直角边OB在x轴上,AO、AB分别与反比例函数y=(k>0,x>0)的图象相交于点C、D , 且C为AO的中点,过点C作x轴的垂线,垂足为E , 连接DE . 若△BDE的面积为 , 则k的值为( )
A、 B、 C、 D、6. 如图,在平面直角坐标系中,O为坐标原点,Rt△OBA的直角边OB在x轴上,AO、AB分别与反比例函数y=(k>0,x>0)的图象相交于点C、D , 且C为AO的中点,过点C作x轴的垂线,垂足为E , 连接DE . 若△BDE的面积为 , 则k的值为( )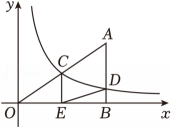 A、 B、 C、5 D、107. 如图,是的弦,过圆心O作于点H,交于点A, , 点M是上异于C,D的一点,连接 , , 则的值是( )
A、 B、 C、5 D、107. 如图,是的弦,过圆心O作于点H,交于点A, , 点M是上异于C,D的一点,连接 , , 则的值是( ) A、 B、 C、 D、8. 如图,已知某山峰的海拔高度为米,一位登山者到达海拔高度为米的点处.测得山峰顶端的仰角为 . 则、两点之间的距离为( )
A、 B、 C、 D、8. 如图,已知某山峰的海拔高度为米,一位登山者到达海拔高度为米的点处.测得山峰顶端的仰角为 . 则、两点之间的距离为( )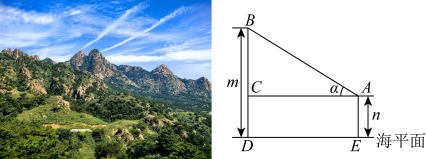 A、米 B、米 C、米 D、米9. 对于抛物线y=2(x﹣1)2+3,下列说法正确的是( )A、抛物线的开口向下 B、抛物线的顶点坐标为(1,3) C、抛物线的对称轴为直线x=﹣1 D、当x>﹣3时,y随x的增大而增大10. 在△ABC中,∠C=90°,tanA , AC=2 , 则BC的长为( )A、1 B、2 C、 D、511. 如图所示,正方形与(其中边 , 分别在 , 轴的正半轴上)的公共顶点在反比例函数的图象上,直线与 , 轴分别相交于点 , . 若这两个正方形的面积之和是 , 且 . 则的值是( )
A、米 B、米 C、米 D、米9. 对于抛物线y=2(x﹣1)2+3,下列说法正确的是( )A、抛物线的开口向下 B、抛物线的顶点坐标为(1,3) C、抛物线的对称轴为直线x=﹣1 D、当x>﹣3时,y随x的增大而增大10. 在△ABC中,∠C=90°,tanA , AC=2 , 则BC的长为( )A、1 B、2 C、 D、511. 如图所示,正方形与(其中边 , 分别在 , 轴的正半轴上)的公共顶点在反比例函数的图象上,直线与 , 轴分别相交于点 , . 若这两个正方形的面积之和是 , 且 . 则的值是( ) A、5 B、1 C、3 D、212. 已知二次函数(a , b , c为常数,)图像的顶点坐标是 , 且经过 , 两点, . 有下列结论:
A、5 B、1 C、3 D、212. 已知二次函数(a , b , c为常数,)图像的顶点坐标是 , 且经过 , 两点, . 有下列结论:①关于x的一元二次方程有两个不相等的实数根;
②当时,y的值随x值的增大而减小;③;
④;⑤对于任意实数t , 总有 .
以上结论正确的有( )
A、5个 B、4个 C、3个 D、2个二、填空题(每题3分,共18分)
-
13. 如图,点A,B,C,D在⊙O上,OC⊥AB,∠AOC=60°,则sin∠BDC的值为.
 14. 已知二次函数 的图象经过点(c,0),但不经过原点,则该二次函数的表达式可以是.(写出一个即可)15. 一块梯形木板 , 按如图方式设计一个矩形桌面(点在边上).当时,矩形桌面面积最大.
14. 已知二次函数 的图象经过点(c,0),但不经过原点,则该二次函数的表达式可以是.(写出一个即可)15. 一块梯形木板 , 按如图方式设计一个矩形桌面(点在边上).当时,矩形桌面面积最大. 16. 如图,在△ABC中,tanC= , D是边BC上一点,将△ACD沿AD翻折得到△AED使线段AE、BC相交于点F若CF=5,EF=2,则AC=.
16. 如图,在△ABC中,tanC= , D是边BC上一点,将△ACD沿AD翻折得到△AED使线段AE、BC相交于点F若CF=5,EF=2,则AC=. 17. 如图,在平面直角坐标系xOy中,点A,B分别在x轴和y轴上,点C为AB的中点,反比例函数的图象经过点C.若点B的坐标为(0,6),OC=5,则.
17. 如图,在平面直角坐标系xOy中,点A,B分别在x轴和y轴上,点C为AB的中点,反比例函数的图象经过点C.若点B的坐标为(0,6),OC=5,则. 18. 如图,在□ABCD中,E是AD上一点,DE=2AE,CE、BA的延长线相交于点F若AB=2,则AF=.
18. 如图,在□ABCD中,E是AD上一点,DE=2AE,CE、BA的延长线相交于点F若AB=2,则AF=.
三、解答题(共6题,共66分)
-
19.(1)、计算:(2)、解方程:x2-2x-1=020. 如图,直线与双曲线交于 , 两点.
 (1)、求和直线的表达式;(2)、根据函数图象直接写出不等式的解集;(3)、求△的面积.21. 如图,点A , B , C , D在⊙O上,BD是直径, , 过点C作CE∥BD交AB的延长线于点E.
(1)、求和直线的表达式;(2)、根据函数图象直接写出不等式的解集;(3)、求△的面积.21. 如图,点A , B , C , D在⊙O上,BD是直径, , 过点C作CE∥BD交AB的延长线于点E.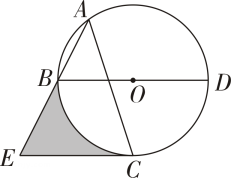 (1)、求证:CE是⊙O的切线.(2)、若 , 求图中阴影部分的面积.22. 四边形ABCD是正方形,点E是边AD上一动点(点D除外)、△EFG是直角三角形,EG=EF,点G在CD的延长线上.
(1)、求证:CE是⊙O的切线.(2)、若 , 求图中阴影部分的面积.22. 四边形ABCD是正方形,点E是边AD上一动点(点D除外)、△EFG是直角三角形,EG=EF,点G在CD的延长线上.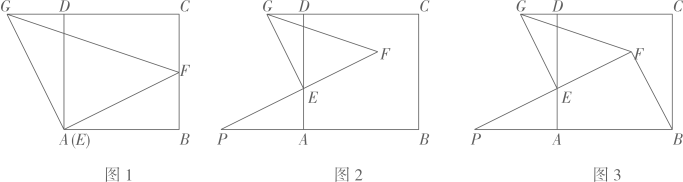 (1)、如图1,当点E与点A重合,且点F在边BC上时,写出BF和DG的数量关系,并说
(1)、如图1,当点E与点A重合,且点F在边BC上时,写出BF和DG的数量关系,并说明理由:
(2)、如图2,当点E与点A不重合,且点F在正方形ABCD内部时,FE的延长线与BA的延长线交于点P,如果EF=EP,写出AE和DG的数量关系,并说明理由;(3)、如图3,在(2)的条件下,连接BF,写出BF和DG的数量关系,并说明理由.23. 综合与实践【主题】雨天撑伞的学问
【情境】图(1)、图(2)是小丽在雨天水平撑伞的示意图,她的身体侧面可以近似看作矩形MNPQ , 米,米,雨伞撑开的宽度米,伞柄的OG部分长为0.45米,点O为AC中点, , 点G到地面的距离是1.35米,手臂可以水平向前最长伸出0.5米,雨线AB与地面的夹角为 , 雨线AB与CD平行,AC与地面BD平行.
 (1)、【问题感知】
(1)、【问题感知】①在图(1)、图(2)中,点C到地面的距离是米;
②如图(1)所示, , 若小丽将伞拿在胸前(OG与NP在同一条直线上),则小丽身体被雨水淋湿的部分米.(参考数据: , , )
(2)、【问题探究】如图(2)所示, , 设小丽将手臂水平前伸了x米(即线段EG的长度),身体被雨水淋湿部分PK的长度为y米,求y与x的函数表达式,并写出头部不被淋湿情况下的取值范围.
(3)、【问题解决】在(2)的条件下,小丽发现水平撑伞身体始终有部分会被淋湿,于是她将雨伞绕点G顺时针旋转一定角度(点G到地面的距离保持不变),使得AC与雨线AB垂直,如图(3)所示,试问:小丽在旋转雨伞后,是否可以通过调节手臂水平前伸长度,使得全身都不会被雨淋湿?如果可以,请求出EG的最小值;如果不可以,请说明理由.
24. 如图,抛物线过点、点 , 交y轴于点C . (1)、求b , c的值.(2)、点是抛物线上的动点
(1)、求b , c的值.(2)、点是抛物线上的动点①当取何值时,的面积最大?并求出面积的最大值;
②过点P作轴,交于点E , 再过点P作轴,交抛物线于点F , 连接 , 问:是否存在点P , 使为等腰直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.