浙江省数学八年级上册期末常考题型真题分类专项特训三

试卷更新日期：2025-12-25 类型：复习试卷

进入出卷网下载

一、三角形中的三线

1. 如图，在锐角 $△ A B C$ 中， $A D$ 为 $B C$ 边上的中线，则（）

A、 $B D = A D$ B、 $B D = C D$ C、 $A D = A C$ D、 $A B = B C$

查看试题解析
2. 如图，为了促进当地旅游发展，某地要在三条公路围城的一块三角形平地 $A B C$ 上修建一个度假村．要使这个度假村到三条公路的距离相等，应该修在（）

A、 $△ A B C$ 三边中线的交点 B、 $△ A B C$ 三个角的平分线的交点 C、 $△ A B C$ 三边高线的交点 D、 $△ A B C$ 三边垂直平分线的交点

查看试题解析
3. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ，以 $A$ 为圆心，任意长为半径画弧，分别交 $A C$ ， $A B$ 于点 $G$ ， $F$ ，再分别以 $G$ ， $F$ 为圆心，大于 $\frac{1}{2} G F$ 长为半径画弧，两弧交于点 $E$ ，作射线 $A E$ ，交 $B C$ 于点 $D$ ，已知 $C D = 3$ ， $A B = 8$ ，则 $△ A B D$ 的面积为（）

A、8 B、10 C、12 D、24

查看试题解析
4. 如图， $B D$ 是 $△ A B C$ 的中线，点E，F分别为 $B D ， C E$ 的中点，若 $△ A E F$ 的面积为 ${4cm}^{2}$ ，则 $△ A B C$ 的面积是 ${cm}^{2}$ ．

查看试题解析
5. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ B A C$ ，过点 $D$ 作 $D E ⊥ A B$ 于点 $E$ ，若 $B C = 9$ ， $D E = 4$ ，则 $B D$ 的长为（）

A、 $4$ B、 $5$ C、 $6$ D、 $7$

查看试题解析
6. 如图，△ABC的三边AB、BC、CA长分别为40、50、60．其三条角平分线交于点O，则S_△ABO：S_△BCO：S_△CAO= ．

查看试题解析

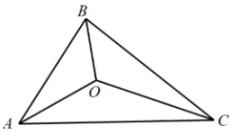
二、三角形面积问题

7. 如图，在数学活动课上，小沐同学画了两个三角形，它们面积之间的关系是（）

A、 $S_{△ A B C} > S_{△ D E F}$ B、 $S_{△ A B C} < S_{△ D E F}$ C、 $S_{△ A B C} = S_{△ D E F}$ D、不能确定

查看试题解析
8. 过 $∠ B A C$ 内一定点D，作一条直线 $E F$ ，交 $A B$ 于点E，交 $A C$ 于点F，下列四种作法， $△ A E F$ 面积最小的是（）

A、 B、 C、 D、

查看试题解析
9. 如图，在 $△ A B C$ 中，点 $D$ ， $E$ ， $F$ 分别是 $B C$ ， $A D$ ， $B E$ 的中点，若 $△ C E F$ 的面积为 $1$ ，则 $△ A B C$ 的面积为( )

A、 $2$ B、 $3$ C、 $4$ D、 $5$

查看试题解析
10. 如图，在 $△ A B C$ 中，已知 $A D$ 平分 $∠ B A C$ ，且 $A D ⊥ B D$ 于点D， $△ A D C$ 的面积是8，则 $△ A B C$ 的面积是．

查看试题解析
11. 如图，在四边形 $A B E D$ 中，点C在边 $A D$ 上，连接 $B C$ ， $B D$ ．已知 $△ A B C ≌ △ D B E$ ，若 $D E = 3$ ， $A D = 10$ ．记 $S_{1} = S_{△ B C D}$ ， $S_{2} = S_{△ A B C} + S_{△ D B E}$ ，则 $S_{1}$ 和 $S_{2}$ 的大小关系是（）

A、 $S_{1} > S_{2}$ B、 $S_{1} = S_{2}$ C、 $S_{1} < S_{2}$ D、无法确定

查看试题解析

三、三角形全等的证明

12. 如图， $A B = A C$ ， $A D = A E$ ，则 $△ A B E ≌ △ A C D$ 的理由是（）

A、 $SAS$ B、 $SSS$ C、 $ASA$ D、 $HL$

查看试题解析
13. 如图，某公园有一个池塘，A，B两点分别位于这个池塘的两端，为测量出池塘的宽AB，小明在池塘的两端分别系上两根绳子AE、BF，两根绳子相交处记为点C，满足CD=CB，AC=EC.连接DE，则线段ED的长即为A，B两点间的距离，此处判定三角形全等的依据是（）

A、SSS B、SAS C、ASA D、AAS

查看试题解析
14. 如图，在四边形 $A B C D$ 中， $A D ∥ B C$ ，连接 $B D$ ，取 $B E = A D$ ，连接 $C E$ ，下列条件中不一定能判定 $△ A B D ≌ △ E C B$ 的是（）

A、 $B D = C B$ B、 $A B = E C$ C、 $∠ A B C = ∠ D E C$ D、 $∠ A B D = ∠ E C B$

查看试题解析
15. 如图，测量一池塘的宽度，测量点B，F，C，E在直线l上，测量点A，D在直线l的异侧，且 $A C = D F$ ， $∠ A = ∠ D$ ， $A B ∥ D E$ ．

(1)、求证： $△ A B C$ ≌ $△ D E F$ ；

(2)、若 $B E = 110$ ， $B F = 30$ ，求 $C F$ 的长．

查看试题解析
16. 如图，在 $△ A B C$ 中，作 $D E ∥ A B$ 分别交于 $A C, B C$ 于点 $D, E$ ，延长 $B C$ 至点 $F$ ，连接 $F D$ ，使得 $∠ F = ∠ A$ ，若 $F D = A C$ ，

(1)、求证： $B C = D E$ ；

(2)、若 $C D$ 平分 $∠ E D F$ ，且 $∠ B = 105 °$ ，求 $∠ D C B$ 的度数．

查看试题解析
17. 如图，点A，D，B，E在一条直线上， $A C = D F$ ， $A D = B E$ ， $∠ A = ∠ E D F$ ，求证： $∠ C = ∠ F$ ．

查看试题解析

四、垂直平分线的应用

18. 如图，在 $△ A B C$ 中， $∠ C = 9 0^{°}$ ， DE垂直平分AB交于 $D$ ，交AB于 $E$ ， $∠ C A D = 4 0^{°}$ ，则 $∠ B$ 等于（）

A、 $4 0^{°}$ B、 $3 0^{°}$ C、 $2 5^{°}$ D、 $1 0^{°}$

查看试题解析
19. 如图，在 $△ A B C$ 中， $A B = 5$ ， $B C = 10$ ， $A C = 9$ ， $M N$ 为边 $B C$ 的垂直平分线，点D为直线 $M N$ 上一动点，则 $△ A B D$ 的周长的最小值为（）

A、10 B、12 C、14 D、15

查看试题解析
20. 小吴在数学实践课上用直尺和圆规作图（如图所示）．已知 $A C = 5$ ， $B C = 12$ ，根据尺规作图痕迹，可求得 $△ A C D$ 的周长是（）

A、24 B、17 C、22 D、19

查看试题解析
21. 如图，在 $△ A B C$ 中，边 $A C$ 的垂直平分线交 $A C$ 于点 $E$ ，交 $B C$ 于点 $D$ ，若 $A B = 6$ ， $△ A B D$ 的周长为18，则 $B C$ 的长为．

查看试题解析