《三角形角的运算》精选压轴题——人教版八年级上学期数学期末复习
试卷更新日期:2025-12-24 类型:复习试卷
一、单选题
-
1. 如图,与的角平分线交于点P, , , 则为( )
 A、 B、 C、 D、2. “三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒 , 组成,两根棒在点相连并可绕转动,点固定, , 点 , 可在槽中滑动,若 , 则的度数是( )
A、 B、 C、 D、2. “三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒 , 组成,两根棒在点相连并可绕转动,点固定, , 点 , 可在槽中滑动,若 , 则的度数是( ) A、60° B、65° C、75° D、80°3. 如图,已知C,A,G三点共线,C,B,H三点共线,2∠CAD=∠BAD,2∠CBD=∠ABD,∠GAE=2∠BAE,∠EBH=2∠EBA,则∠D和∠E的关系满足( )
A、60° B、65° C、75° D、80°3. 如图,已知C,A,G三点共线,C,B,H三点共线,2∠CAD=∠BAD,2∠CBD=∠ABD,∠GAE=2∠BAE,∠EBH=2∠EBA,则∠D和∠E的关系满足( ) A、2∠E+∠D=320° B、2∠E+∠D=340° C、2∠E+∠D=360° D、2∠E+∠D=300°4. 如图,在中,将沿直线m翻折,点B落在点D的位置,若 , 则的度数是( )
A、2∠E+∠D=320° B、2∠E+∠D=340° C、2∠E+∠D=360° D、2∠E+∠D=300°4. 如图,在中,将沿直线m翻折,点B落在点D的位置,若 , 则的度数是( ) A、 B、 C、 D、60°5. 如图,在中, , , 的平分线与的垂直平分线交于点 , 将沿(在上,在上)折叠,点与点恰好重合,则为( )
A、 B、 C、 D、60°5. 如图,在中, , , 的平分线与的垂直平分线交于点 , 将沿(在上,在上)折叠,点与点恰好重合,则为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
6. 如图,在△ABC中,∠A=58°,∠B=80°,将纸片的一角折叠,使顶点C落在△ABC 外点C'处,若∠2=26°,则∠1度数是°.
 7. 如图,在中, , , 是射线上的一个动点,连接 , 将沿着翻折得到 , 当的三边与的三边有一组边垂直时,则 .
7. 如图,在中, , , 是射线上的一个动点,连接 , 将沿着翻折得到 , 当的三边与的三边有一组边垂直时,则 . 8. 如图,中, , 点D为边上一点,将沿直线折叠后,若 , 则的度数为 .
8. 如图,中, , 点D为边上一点,将沿直线折叠后,若 , 则的度数为 . 9. 如图,将沿直线折叠,使顶点的对应点落在边上,此时直线与边 , 分别相交于点 , . 若 , 则的度数为 .
9. 如图,将沿直线折叠,使顶点的对应点落在边上,此时直线与边 , 分别相交于点 , . 若 , 则的度数为 . 10. 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=
10. 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=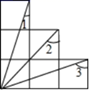 11. 如图,将三角形纸片沿折叠,使点落在点处,连接 , 平分 , 平分 , 若 , 则的度数为 .
11. 如图,将三角形纸片沿折叠,使点落在点处,连接 , 平分 , 平分 , 若 , 则的度数为 . 12. 如图,△ABC是边长为4cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿线段AB,BC运动,且它们的速度都为1cm/s.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s).当t= 时,△PBQ是直角三角形.
12. 如图,△ABC是边长为4cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿线段AB,BC运动,且它们的速度都为1cm/s.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s).当t= 时,△PBQ是直角三角形. 13. 如图,在中, , 、、分别平分的外角 , 内角 , 外角 , 以下结论:①;②;③;④ , 其中正确的结论有 .
13. 如图,在中, , 、、分别平分的外角 , 内角 , 外角 , 以下结论:①;②;③;④ , 其中正确的结论有 .
三、解答题
-
14. 如图,四边形ABCD,BE、DF分别平分四边形的外角∠MBC和∠NDC,若∠BAD=α,∠BCD=β.
 (1)、如图1,若α+β=105°,求∠MBC+∠NDC的度数;(2)、如图1,若BE与DF相交于点G,∠BGD=45°,请直接写出α,β所满足的数量关系式;(3)、如图2,若α=β,判断BE,DF的位置关系,并说明理由.15. 在△ABC中,∠C>∠B.
(1)、如图1,若α+β=105°,求∠MBC+∠NDC的度数;(2)、如图1,若BE与DF相交于点G,∠BGD=45°,请直接写出α,β所满足的数量关系式;(3)、如图2,若α=β,判断BE,DF的位置关系,并说明理由.15. 在△ABC中,∠C>∠B.
 (1)、如图1,AE、AD分别是△ABC的高和角平分线,若∠B=40°,∠C=80°,求∠DAE的度数;(2)、如图2,AD平分∠BAC,P是AD延长线上一点,过P作PE⊥BC,直接写出∠P与∠C,∠B的数量关系 .16. 如图所示,AB,CD相交于点O,∠A=48°,∠D=46°.
(1)、如图1,AE、AD分别是△ABC的高和角平分线,若∠B=40°,∠C=80°,求∠DAE的度数;(2)、如图2,AD平分∠BAC,P是AD延长线上一点,过P作PE⊥BC,直接写出∠P与∠C,∠B的数量关系 .16. 如图所示,AB,CD相交于点O,∠A=48°,∠D=46°. (1)、若BE平分∠ABD交CD于F,CE平分∠ACD交AB于G,则∠BEC的度数为;(2)、延长AC至点H,若直线BM平分∠ABD交CD于F,CM平分∠DCH交直线BF于M,求∠BMC的度数.17. 【问题背景】
(1)、若BE平分∠ABD交CD于F,CE平分∠ACD交AB于G,则∠BEC的度数为;(2)、延长AC至点H,若直线BM平分∠ABD交CD于F,CM平分∠DCH交直线BF于M,求∠BMC的度数.17. 【问题背景】(1)如图1的图形我们把它称为“8字形”,请说明;
【简单应用】
(2)如图2,分别平分 , 若 , 求的度数;
【问题探究】
(3)如图3,直线平分的外角平分的外角 , 若 , 请猜想的度数,并说明理由.
【拓展延伸】
(4)在图4中,若设 , 平分平分的外角 , 猜想与的关系,直接写出结论(用表示).
 18.
18.【问题呈现】
小明在学习中遇到这样一个问题:
如图1,在中, , 平分 , 于D,猜想、、的数量关系.
 (1)小明阅读题目后,没有发现数量关系与解题思路.于是尝试代入、的值求值,得到下面几组对应值:
(1)小明阅读题目后,没有发现数量关系与解题思路.于是尝试代入、的值求值,得到下面几组对应值:/度
10
30
30
20
20
/度
70
70
60
60
80
/度
30
a
15
20
30
上表中 ▲ , 于是得到与、的数量关系为 ▲ .
【变式应用】
(2)小明继续研究,在图2中, , , 其他条件不变,若把“于D”改为“F是线段上一点,于D”,求的度数,并写出与、的数量关系:【思维发散】
(3)小明突发奇想,交换B、C两个字母位置,在图3中,若把(2)中的“点F在线段上”改为“点F是延长线上一点”,其余条件不变,当 , 时,∠F度数为 ▲ °.【能力提升】
(4)在图4中,若点F在 的延长线上,于D, , , 其余条件不变,从别作出 和的角平分线,交于点P,试用 x、y表示 ▲ .19. 定义:在一个三角形中,如果有一个角是另一个角的 , 我们称这两个角互为“友爱角”,这个三角形叫作“友爱三角形”.例如:在△ABC中,如果∠A=80°,∠B=40°,那么∠A与∠B互为“友爱角”,△ABC为“友爱三角形”. (1)、如图1,△ABC是“友爱三角形”,且∠A与∠B互为“友爱角”(∠A>∠B),∠ACB=90°.
(1)、如图1,△ABC是“友爱三角形”,且∠A与∠B互为“友爱角”(∠A>∠B),∠ACB=90°.
①求∠A、∠B的度数.
②若CD是△ABC中AB边上的高,则△ACD、△BCD都是“友爱三角形”吗?为什么?
(2)、如图2,在△ABC中,∠ACB=70°,∠A=66°,D是边AB上一点(不与点A , B重合),连接CD , 若△ACD是“友爱三角形”,直接写出∠ACD的度数.
四、实践探究题
-
20. 【原题再现】课本第42页有这样一道题:
如图1,将△ABC纸片沿DE折叠,使点A落在四边形BCDE内点的位置.试探索∠A与∠1+∠2之间的数量关系,并说明理由.

小明提出一种正确的解题思路:
连接 , 则∠1、∠2分别为、的外角,……
请你按照小明的思路解决上述问题.
【变式探究】如图2,若将原题中“点A落在四边形BCDE内点A'的位置”变为“点A落在四边形BCDE外点的位置”,试猜想此时∠A与∠1、∠2之间的数量关系,并说明理由.
【结论运用】将四边形纸片ABCD( , AB与CD不平行)沿EF折叠成图3的形状,若 , , 请直接写出∠ABC的度数.