浙江省数学七年级上册期末常考题型真题分类专项特训五

试卷更新日期：2025-12-15 类型：复习试卷

进入出卷网下载

一、代数式的几何问题

1. 在长方形 $A B C D$ 中放入3个正方形如图所示，若 $A I = C J$ ， $M N = P Q$ ，则知道下列哪条线段的长就可以求出图中阴影部分的周长和（）

A、 $B F$ B、 $E H$ C、 $A B$ D、 $B C$

查看试题解析
2. 如图1，两个正方形分别由①，②两种规格小长方形纸片拼成，现将它们放入一个长为a，宽为b的大长方形中，如图2，其中阴影部分恰好为正方形，则大长方形中未被纸片覆盖部分甲的周长为 .（用含a，b的代数式表示）

查看试题解析
3. 如图，长为 $y$ 、宽为 $x$ 的大长方形被分割为7个小长方形，除阴影 $A$ ， $B$ 外，其余5个是形状、大小完全相同的小长方形，其宽为4．下列说法：①小长方形的长为 $y - 12$ ；②阴影 $A$ 的宽和阴影 $B$ 的宽和为 $x - y + 4$ ；③若 $x$ 为定值，则阴影 $A$ 和阴影 $B$ 的周长为定值．其中正确的是（）

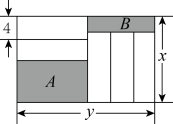A、①③ B、②③ C、①② D、①②③

查看试题解析
4. 如图，在一个大长方形中放入了标号为①，②，③，④，⑤五个四边形，其中①，②为两个长方形，③，④，⑤为三个正方形，相邻图形之间互不重叠也无缝隙．若想求得长方形②的周长，甲、乙、丙、丁四位同学提出了自己的想法：
甲说：只需要知道①与③的周长和；
乙说：只需要知道①与⑤的周长和；
丙说：只需要知道③与④的周长和；
丁说：只需要知道⑤与①的周长差；
下列说法正确的是（）

A、只有甲正确 B、甲和乙均正确 C、乙和丙均正确 D、只有丁正确

查看试题解析
5. 如图，将图1中的长方形纸片剪成①号、②号、③号、④号正方形和⑤号长方形，并将它们按图2的方式无重叠地放入另一个大长方形中，若需求出没有覆盖的阴影部分的周长，则下列说法中错误的是（　　）

A、只需知道③号正方形的边长即可 B、只需知道④号正方形的边长即可 C、只需知道⑤号长方形的周长即可 D、只需知道图1中大长方形的周长即可

查看试题解析
6. 如图，在正方形 $A B C D$ 中放入正方形 $A E F G$ 和正方形 $B H I E$ ，点 $E$ 在 $A B$ 上，且点 $F, I, E$ 在一条直线上．若阴影部分面积为 $6 x, D G = 2$ ，则阴影部分周长为．（用含 $x$ 的代数式表示）

查看试题解析

二、代数式一题多解

7. 已知 $| x | = 2 ， | y | = 5 ，$ 且 $x ＞ y ，$ 则 $x + y =$ .

查看试题解析
8. 已知 $| a | = 9 ， | b | = 3$ ，则 $| a - b | = b - a$ ，则 $a + b$ 的值．

查看试题解析
9. 若 $| a | = 3$ ， $| b | = 4$ ，且 $a$ ， $b$ 异号，则 $| a + b | =$ ．

查看试题解析
10. 已知有理数 $x$ ， $y$ 满足： $| x - 2 | = 3$ ， ${(y + 1)}^{2} = 4$ 且 $| x + y | = x + y$ ，则 $x - y =$ ．

查看试题解析
11. 已知 $a^{2} + b c = 14 ， b^{2} - 2 b c = - 6$ ，则 $3 a^{2} + 4 b^{2} - 5 b c$ =.

查看试题解析
12. 已知 $|a| = 1$ ， $|b| = 2$ ， $|c| = 3$ ，且 $a > b > c$ ，那么 $a + b - c =$ ．

查看试题解析
13. 已知 $A = 3 x + x y - 2 y$ ，小明在计算 $2 A - B$ 时，误将其按 $2 A + B$ 计算，结果得到 $7 x + 4 x y - y$ ．

(1)、求多项式 $B$ ．

(2)、求 $2 A - B$ 的正确结果是多少？

查看试题解析
14. 已知 4 个互不相等的非零整数 $a, b, c, d$ 满足 $a^{2} + b^{2} + c^{5} + d^{2025} = {(2 \times 0 + 2 \times 5)}^{2}$ ，其中 $c > 0, |d| \leq 1$ ，则 $a + b + c + d$ 的最小值是．

查看试题解析

三、定义新运算

15. 四四跟同学在某餐厅吃饭，如图为此餐厅的菜单，若他们所点的餐点总共为16份意大利面，x杯饮料，y个蛋挞，则他们点了几份A餐
A餐：一份意大利面
B餐：一份意大利面加一杯饮料
C餐：一份意大利面加一杯饮料与两个蛋挞

A、16-x B、16-x- $\frac{y}{2}$ C、16- $\frac{y}{2}$ D、16-x+ $\frac{y}{2}$

查看试题解析
16. 对任意一个三位正整数 $m$ ，如果 $m$ 的百位数字等于十位数字的2倍与个位数字之和，那么称这个数 $m$ 为“神奇数”．例如： $m = 311$ ，因为 $1 \times 2 + 1 = 3$ ，所以311是“神奇数”．例如： $m = 514$ ，因为 $1 \times 2 + 4 = 6 \neq 5$ ，所以514不是“神奇数”．

(1)、判断917和642是不是“神奇数”，并说明理由；

(2)、若 $m$ 是“神奇数”，且 $m$ 与13的和能被11整除，求满足条件的所有“神奇数” $m$ ．

查看试题解析
17. 定义运算： $a ※ b = b - 2 a$ ，下面给出了关于这种运算的四个结论：
① $(- 2) ※ (- 5) = - 1$ ； ② $a ※ b = b ※ a$ ；
③若 $a + b = 0$ ，则 $(a ※ a) + (b ※ b) = 0$ ； ④若 $3 ※ x = 0$ ，则 $x = 6$ ．
其中，正确结论的序号是（填上你认为所有正确结论的序号）．

查看试题解析
18. 小明有以下8张卡牌，第一组卡牌上标有数，第二组卡牌上标有多项式，请你根据要求完成以下任务．
任务1：请在第一组卡牌中选择3张卡牌，使所标数的积最小，请列出算式并求得结果；
任务2：请在第一组中选择1张卡牌，在第二组中选择2张卡牌，使这3张卡牌上所标的数与多项式相加，化简后结果为二项式，请列出算式并求其结果．

查看试题解析
19. 有一个数值转换器，运算流程如下：

(1)、在 $- 1$ ， 2，4，16中选择3个合适的数分别输入 $x$ ，求对应输出 $y$ 的值．

(2)、若输出 $y$ 的值为 $- \sqrt{3}$ ，求输入 $x$ 的值．

查看试题解析

四、代数式的应用

20. 某学校准备在网上订购一批某品牌羽毛球拍和羽毛球，在查阅网店后发现该品牌羽毛球拍每副定价100元，羽毛球每个定价5元，现有甲，乙两家网店均提供包邮服务，并提出了各自的优惠方案：
甲网店：买1副羽毛球拍送3个羽毛球；
乙网店：羽毛球拍与羽毛球都按定价的 $90 %$ 付款．
已知学校要购买羽毛球拍20副，羽毛球 $x$ 个（ $x > 60$ ）．

(1)、若在甲网店购买，需付款______元；若在乙网店购买，需付款______元；（用含x的式子表示）

(2)、若 $x = 100$ 时，请你通过计算，说明此时在哪家网店购买较为合算？

(3)、若 $x = 150$ 时，你能给出一种最省钱的购买方案吗？请说明理由．

查看试题解析
21. 某种窗户由上下两部分组成，其上部是用木条围成的半圆形，且半圆形内部由三根等长的木条分隔，下部是用木条围成的边长相等的四个小正方形，木条的宽度和厚度不计．已知下部每个小正方形的边长为a米．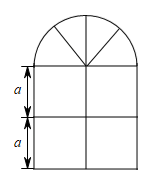

(1)、用含a的代数式分别表示窗户的面积和所用木条的总长度；

(2)、若 $a = 1$ 米，窗户上安装的是玻璃，玻璃25元/平方米，木条20元/米，求制作这个窗户需要的总钱数（ $π$ 值取3，计算结果精确到个位）．

查看试题解析
22. A，B，C，D四个车站的位置如图所示，车站 B 距车站A，D的距离分别为 $(a + b) k m$ ，
$(5 a + 3 b) k m$ ，车站C 与车站D 的距离为(3a+2b) km.其中a，b均是不为0的实数.

(1)、求B，C两站之间的距离(用含a，b的代数式表示).

(2)、若B，D两个车站之间的距离比A，B两个车站之间的距离长8km，求出B，C两个车站相距多少千米.

查看试题解析
23. 如图，用三种大小不同的五个正方形和一个长方形（图中阴影部分）拼成长方形 $A B C D$ ，已知 $E F = 7 cm$ ，较小正方形的边长为 $x cm$ ．

(1)、填空： $F G =$ __________ $cm$ ， $D G =$ __________ $cm$ （用含有 $x$ 的代数式分别表示）．

(2)、先用含有 $x$ 的代数式表示出长方形 $A B C D$ 的周长．当 $x = 9 cm$ 时，求长方形 $A B C D$ 的周长．

查看试题解析