《二次函数》精选压轴题（一）—浙江省九（上）数学期末复习

试卷更新日期：2025-12-14 类型：复习试卷

进入出卷网下载

一、选择题

1. 已知抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的顶点在第一象限，且过点 $(0, 1)$ 和 $(- 1, 0)$ ，则 $P = a + b + c$ 的值的范围是（）

A、 $- 1 < P < 0$ B、 $- 1 < P < 1$ C、 $1 < P < 2$ D、 $0 < P < 2$

查看试题解析
2. 二次函数 $y = a x^{2} + b x + c$ （ $a$ ， $b$ ， $c$ 为常数，且 $a \neq 0$ ），满足 $a - b = a b = c$ ，则以下结论正确的是（）

A、若 $a = - 2$ ，该函数图象经过点 $(1, 2)$ B、若 $c = 2$ ，该函数图象经过点 $(1, 2)$ C、若 $a$ ， $b$ ， $c$ 的绝对值相等，则该函数图象可能经过点 $(1, 2)$ D、若 $a$ ， $b$ ， $c$ 中有两数相等，则该函数图象可能经过点 $(1, 2)$

查看试题解析
3. 已知抛物线 $y = a x^{2} - 2 a x (a > 0)$ 经过点 $A (m, y_{1})$ ， $B (m + 1, y_{2})$ ，若 $y_{1} < y_{2} < 0$ ，则 $m$ 的取值范围是（）

A、 $m > \frac{1}{2}$ B、 $\frac{1}{2} < m < 1$ C、 $\frac{1}{2} < m < 2$ D、 $1 < m < 2$

查看试题解析
4. 已知抛物线 $y = a {(x + 1)}^{2} + b$ 经过点 $P (x_{1}, y_{1})$ ， $Q (x_{2}, y_{2})$ ，且 $|x_{1} + 1| < |x_{2} + 1|$ ，则下列不等式一定成立的是（）

A、 $y_{1} - y_{2} > 0$ B、 $y_{1} - y_{2} < 0$ C、 $a (y_{1} - y_{2}) > 0$ D、 $a (y_{1} - y_{2}) < 0$

查看试题解析
5. 已知二次函数 $y = - (x - a) (x - b) + 3 (a, b$ 是实数，且 $a \neq b)$ ，设该函数的最大值为 $k$ ，则下列说法正确的是（）

A、若 $3 < a < 5, 3 < b < 5$ ，则 $k < 3$ B、若 $3 < a < 5, 3 < b < 5$ ，则 $k > 4$ C、若 $3 < a < 5, 5 < b < 7$ ，则 $k > 3$ D、若 $3 < a < 5, 5 < b < 7$ ，则 $3 < k < 7$

查看试题解析
6. 已知抛物线 $y = a x^{2} + b x + b - a (a < 0)$ ，当 $- 1 \leq x \leq 4$ 时，最大值与最小值的差为 $a^{2}$ ，若将抛物线向左平移4个单位后经过点 $(- 1, 0)$ ，则a的值为（）

A、 $- 8$ B、 $- 9$ C、 $- 10$ D、 $- 11$

查看试题解析
7. 如图，二次函数 $y = a x^{2} + b x + c (a > 0)$ 的图象与 $x$ 轴的正半轴交于点 $A (m, 0), m < 3$ ，与 $y$ 轴的负半轴交于点 $B$ ，对称轴为直线 $x = 1$ ．其中判断错误的是（）

A、 $3 a + c > 0$ B、若点 $P (4, 2 n), Q (- 1, 4 n + 2)$ 在图象上，则 $n < - 1$ C、 $3 b < 2 c$ D、若点 $P (1 + 2 k, 2 n)$ ， $Q$ $(1 - 2 k, 4 n + 2)$ 在图象上，则 $a - c \geq 2$

查看试题解析
8. 如图，在边长为 $6$ 的正方形 $A B C D$ 中，点 $E$ ， $F$ 分别为边 $A D$ ， $C D$ 上的点，且 $A E = D F$ ， $B F$ 与 $C E$ 交于点 $G$ ，连结 $E F$ ．取 $E F$ 的中点 $M$ ，连结 $D M$ ， $G M$ ，则 $D M + G M$ 的最小值为（）

A、6 B、 $3 \sqrt{2}$ C、3 D、 $3 \sqrt{5} - 3$

查看试题解析
9. 如图，在平面直角坐标系中 $y = - \frac{3}{4} (x - 4) (x + 1)$ ，与 $x$ 轴交于 $A, B$ 两点（A在 $B$ 的左侧），与 $y$ 轴交于点 $C$ ，点 $P$ 是 $B C$ 上方抛物线上一点，连结 $A P$ 交 $B C$ 于点 $D$ ，连结 $A C, C P$ ，记 $△ A C D$ 的面积为 $S_{1}$ ， $△ P C D$ 的面积为 $S_{2}$ ，则 $\frac{S_{2}}{S_{1}}$ 的最大值为（）

A、 $\frac{3}{4}$ B、 $\frac{3}{5}$ C、 $\frac{4}{5}$ D、1

查看试题解析
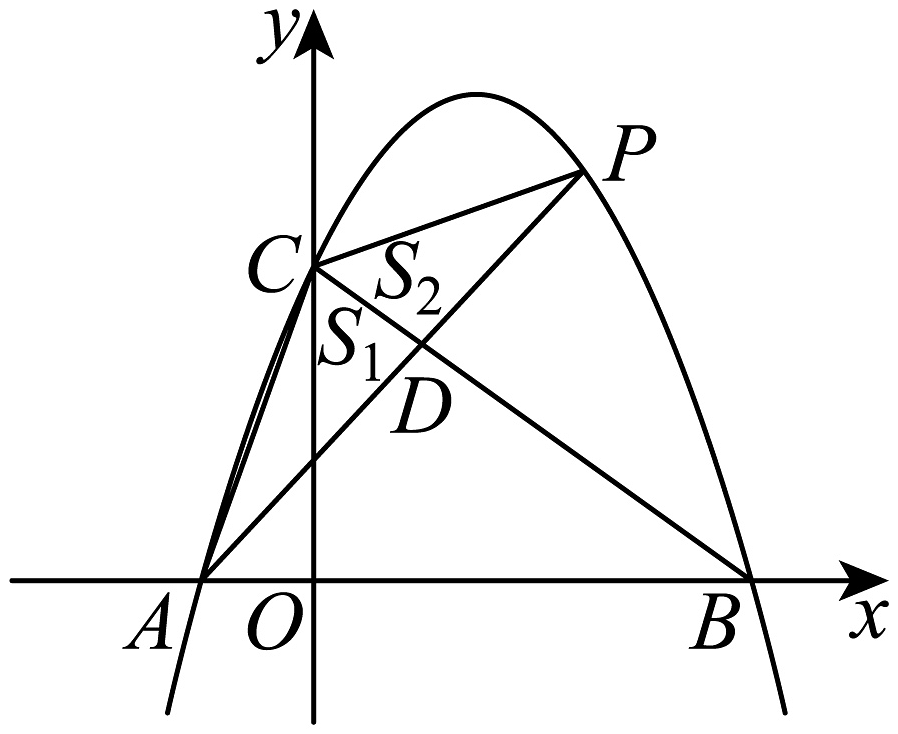10. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ ，图象的一部分如图所示，该函数图象经过点 $(- 2, 0)$ ，对称轴为直线 $x = - \frac{1}{2}$ 对于下列结论：① $a b c < 0$ ；② $2 a + c = 0$ ；③ $a m^{2} + b m < \frac{1}{4} (a - 2 b)$ （其中 $m \neq - \frac{1}{2}$ ）；④若 $A (x_{1}, y_{1})$ 和 $B (x_{2}, y_{2})$ 均在该函数图象上，且 $x_{1} > x_{2} > 1$ ，则 $y_{1} > y_{2}$ 其中正确结论的个数共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 在直角坐标系中，二次函数 $y = 2 x^{2} - 4 x + c$ 的图象过点 $A (2, y_{1})$ ，点 $B (- 2, y_{2})$ ，点 $C (m, n)$ ．若 $y_{1} < n < y_{2}$ ，则 $m$ 的取值范围是．

查看试题解析
12. 已知抛物线 $y = - \frac{1}{2} x^{2} + b x + 4$ （ $b$ 为常数），直线 $L : y = b + 4$ ，当 $x \leq \frac{1}{2} b$ 时，抛物线的最高点到直线 $L$ 的距离为2，则 $b$ 的值是

查看试题解析
13. 在平面直角坐标系中，我们称 $|y| = - x^{2} + m (- \sqrt{m} \leq x \leq \sqrt{m})$ 为“m蛋型”抛物线，如： $|y| = - x^{2} + 2 (- \sqrt{2} \leq x \leq \sqrt{2})$ 称“2蛋型”抛物线，如图所示，点A在“4蛋型”抛物线的第一象限上，其横坐标为1，现将“4蛋型”抛物线绕O点顺时针旋转 $θ$ 度，A旋转后的对应点为 $A^{'}$ ，过 $A^{'}$ 作x轴的平行线，交旋转后的“4蛋型”抛物线于 $B^{'}$ ，若 $\tan θ = 2$ ，则 $A^{'} B^{'}$ 的值是．

查看试题解析
14. 如图1，在扇形 $O A B$ 中，点P从A点出发，沿 $\overset{⌢}{A B}$ 运动至B点，再沿线段 $B O$ 运动至O点．当点P运动到B点时，点Q从O点出发，沿 $O A$ 方向运动（当点P到达O点时，P，Q同时停止运动）．已知 $∠ A O B = 135 °$ ，点P的速度为5个单位长度每秒，点Q的速度为4个单位长度每秒．P点到O点的距离d与运动时间t（秒）的关系如图2所示．
（1）m的值为．
（2） $△ P Q O$ 面积的最大值为．

查看试题解析

三、解答题

15. 定义：对于点 $P (m, p)$ 与拋物线 $y = a x^{2} + b x + c$ 上一点 $Q (m, q)$ ，若 $| p - q | \leq 1$ ，则称点 $P (m, p)$ 为抛物线 $y = a x^{2} + b x + c$ 的一个纵邻点．例如：对于点 $(2, 3.5)$ 和抛物线 $y = x^{2}$ 上的点 $(2, 4)$ 满足 $| 3.5 - 4 | \leq 1$ ，则点 $(2, 3.5)$ 是拋物线 $y = x^{2}$ 的一个纵邻点．

(1)、试判断 $(1, 3)$ 是不是拋物线 $y = 2 x^{2} - 1$ 的纵邻点，并说明理由；

(2)、若 $E (e, 6)$ ， $F (f, 6)$ 都是抛物线 $y = 2 x^{2} - 1$ 的纵邻点，求 $e - f$ 的最大值；

(3)、若点A坐标为 $(n, h)$ ，点B坐标为 $(n + 1, h)$ ，线段 $A B$ 上的所有点都是拋物线 $y = {(x - 2)}^{2} + 1$ 的纵邻点，求h的最大值和最小值，以及相应的n的值．

查看试题解析