《三角形的综合》精选压轴题（二）—浙江省八（上）数学期末复习

试卷更新日期：2025-12-14 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图，在 $△ A B C$ 中， $A C = 2$ ， $A B = 4$ ，分别以 $A C$ ， $B C$ 为边向外作正 $△ A C D$ 和正 $△ B C E$ ，连结 $A E$ ，在 $△ A B C$ 的边 $B C$ 变化过程中，当 $A E$ 取最长时，则 $B C$ 的长为（）

A、 $2 \sqrt{7}$ B、 $\sqrt{29}$ C、 $\sqrt{19}$ D、 $2 \sqrt{5}$

查看试题解析
2. 如图，正方形 $A B C D$ 是由四个全等的直角三角形和小正方形 $E F G H$ 拼成，连接 $A C$ ， $E C$ ，若想求出图中阴影部分的面积，只需知道（）

A、 $A B$ 的长 B、 $A E$ 的长 C、 $E F$ 的长 D、 $C E$ 的长

查看试题解析
3. 如图，在 $△ A B C$ 中， $D$ 为 $A C$ 上一点， $B D = C D$ ， $E$ 为 $B D$ 上一点， $∠ A = ∠ D E C$ ，若要求 $△ A B D$ 和 $△ E C D$ 的周长之差，则只需要知道（）

A、 $A D - E D$ 的值 B、 $A B - E D$ 的值 C、 $B C - B E$ 的值 D、 $C D - B E$ 的值

查看试题解析
4. 如图， $C$ 为线段 $A E$ 上一动点（不与点 $A$ ， $E$ 重合），在 $A E$ 同侧分别作等边 $△ A B C$ 和等边 $△ C D E$ ， $A D$ 与 $B E$ 交于点 $O$ ， $A D$ 与 $B C$ 交于点 $P$ ， $B E$ 与 $C D$ 交于点 $Q$ ，连接 $P Q$ ，下列结论错误的是（）

A、 $A D = B E$ B、 $∠ D O E = 60 °$ C、 $D E = D P$ D、 $P Q ∥ A E$

查看试题解析
5. 如图，在平面直角坐标系中，点 $A (- 3, 0), B (0, 3 \sqrt{3}) ， C$ 为y轴上一动点，当 $A C + \frac{1}{2} B C$ 取到最小值时，点C的纵坐标为（）

A、 $\frac{3}{2} \sqrt{3}$ B、 $\frac{2 \sqrt{3}}{3}$ C、 $\sqrt{3}$ D、 $\sqrt{5}$

查看试题解析
6. 如图，在 $Rt △ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ C A B$ 交 $B C$ 于点 $D$ ，点 $E$ 在边 $A B$ 上， $A E = B E = B D$ ， $D E = \frac{2}{3}$ ，则 $A D$ 的长度为（）

A、 $\sqrt{2}$ B、 $\frac{4}{3}$ C、 $\frac{3}{2}$ D、 $\sqrt{3}$

查看试题解析
7. 如图，在 $△ A B C$ 中， $A B = A C = 5$ ， $B C = 8$ ，点 $D$ 在 $A B$ 边上，连结 $C D$ ．点 $E$ 是 $C D$ 的中点，连接 $A E$ ．若 $A B ⊥ A E$ ，则 $A E$ 的长是（）

A、2 B、 $\frac{12}{5}$ C、 $\frac{5}{2}$ D、 $\frac{8}{3}$

查看试题解析
8. 如图，在等边 $△ A B C$ 中， $B F$ 是 $A C$ 边上的中线，点D在 $B F$ 上，连接 $A D$ ，在 $A D$ 的右侧作等边 $△ A D E$ ，连接 $E F$ ，当 $△ A E F$ 周长最小时，则 $∠ F A E$ 的大小是（）

A、 $30 °$ B、 $45 °$ C、 $60 °$ D、 $90 °$

查看试题解析
9. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A D$ 是 $B C$ 边上的高线， $E F$ 垂直平分 $A B$ ，分别交 $A B$ ， $A C$ ， $A D$ 于点 $E$ ， $F$ ， $G$ ．若 $∠ B A C = 45 °$ ， $E G = 1$ ，则 $C F =$ （）

A、 $\sqrt{2}$ B、 $\frac{7}{5}$ C、 $\frac{4}{3}$ D、 $\frac{3}{2}$

查看试题解析
10. 如图，在直角坐标系中，点 $A$ 、 $B$ 分别是 $x$ 轴、 $y$ 轴上的两个动点，分别以 $O B$ 、 $A B$ 为直角边在第一、第二象限作等腰直角 $△ B O D$ 和等腰直角 $△ A B C$ ，连接 $C D$ 交 $y$ 轴于点 $P$ ，连接 $C O$ 、 $A D$ ．下列说法：① $△ B C O$ ≌ $△ B A D$ ；② $C O ⊥ A D$ ；③ $P C = P D$ ；④若 $A (- 8, 0)$ ，则 $B P = 4$ ．其中正确的有（）

A、①②④ B、①②③ C、①③④ D、①②③④

查看试题解析

二、填空题

11. 如图， $△ A B C$ 中， $A C = B C$ ， $B E ⊥ A C$ ， E为垂足，点D在 $B C$ 上，且 $A B = A D$ ，若 $C E = 3 C D$ ， $A E = 2$ ，则 $B C$ 的长为．

查看试题解析
12. 如图，在等腰 $Rt △ A B C$ 中， $A B = B C = 5$ ， $∠ A B C = 90 °$ ， D是射线 $B C$ 上一点，连结 $A D$ ，过点A作 $A E ⊥ A D, A E = A D$ ，连结 $C E$ 与直线 $A B$ 交于点F，若 $A B = 4 B F$ ，则 $B D$ 的长是．

查看试题解析
13. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 100 °$ ，点 $D$ 为三角形内部一点且 $∠ B D C = 140 °$ ，点 $E$ 为 $B C$ 中点，连接 $A D$ ， $D E$ ，作 $∠ F D C = ∠ E D C$ ，且 $D F = 2 D E$ ，当 $∠ A D B =$ 时， $△ D F C$ 为直角三角形．

查看试题解析
14. 如图，在 $△ A B C$ 中， $A B = A C, ∠ B A C = 80^{\circ}, D$ 是边 $B C$ 上一点（不与 $B, C$ 重合）， $∠ D A C$ 和 $∠ B C A$ 的角平分线交于点 $E$ ．

(1)、若 $∠ B A D = 20^{\circ}$ ，则 $∠ A E C$ 的度数为；

(2)、记 $∠ D A E$ 和 $∠ A C E$ 的度数之和为 $m$ ，则 $m$ 的取值范围为．

查看试题解析
15. 如图，在四边形 $A B C D$ 中，对角线 $A C ⊥ B D$ ， F为 $C D$ 上一点，连接 $A F$ 交 $B D$ 于点E， $A F ⊥ A B$ ，已知 $∠ B A G = ∠ A B C = 45^{\circ}$ ，且 $B C + A G = 10 \sqrt{2}$ ．
（1）则 $A B$ 的长是；
（2）若 $A E = 2 E F$ ，且 $∠ A G D + ∠ B C D = 180^{\circ}$ ，则 $A F =$ ．

查看试题解析

三、综合题

16. 如图，在等腰锐角 $△ A B C$ 中， $A B = A C$ ， $C D$ 为 $A B$ 边上的高线， $E$ 为 $A C$ 边上的点，连接 $B E$ 交 $C D$ 于点 $F$ ，设 $∠ B C D = α$ ．

(1)、用含 $α$ 的代数式表示 $∠ A$ ；

(2)、若 $C E = C F$ ，求 $∠ E B C$ 的度数；

(3)、在（ $2$ ）的条件下，若 $E$ 为 $A C$ 中点， $A B = A C = 2 \sqrt{5}$ ，求 $△ A B C$ 的面积．

查看试题解析
17. 如图，在 $△ A B C$ 中， $∠ C = 9 0^{°}, 6 0^{°} < ∠ A B C < 9 0^{°}$ .点 $E$ 在边AB上，点 $D$ 在CB延长线，且满足 $B D = B E$ .连接 $D E, A D$ .已知 $∠ C A D = ∠ B E D$ .

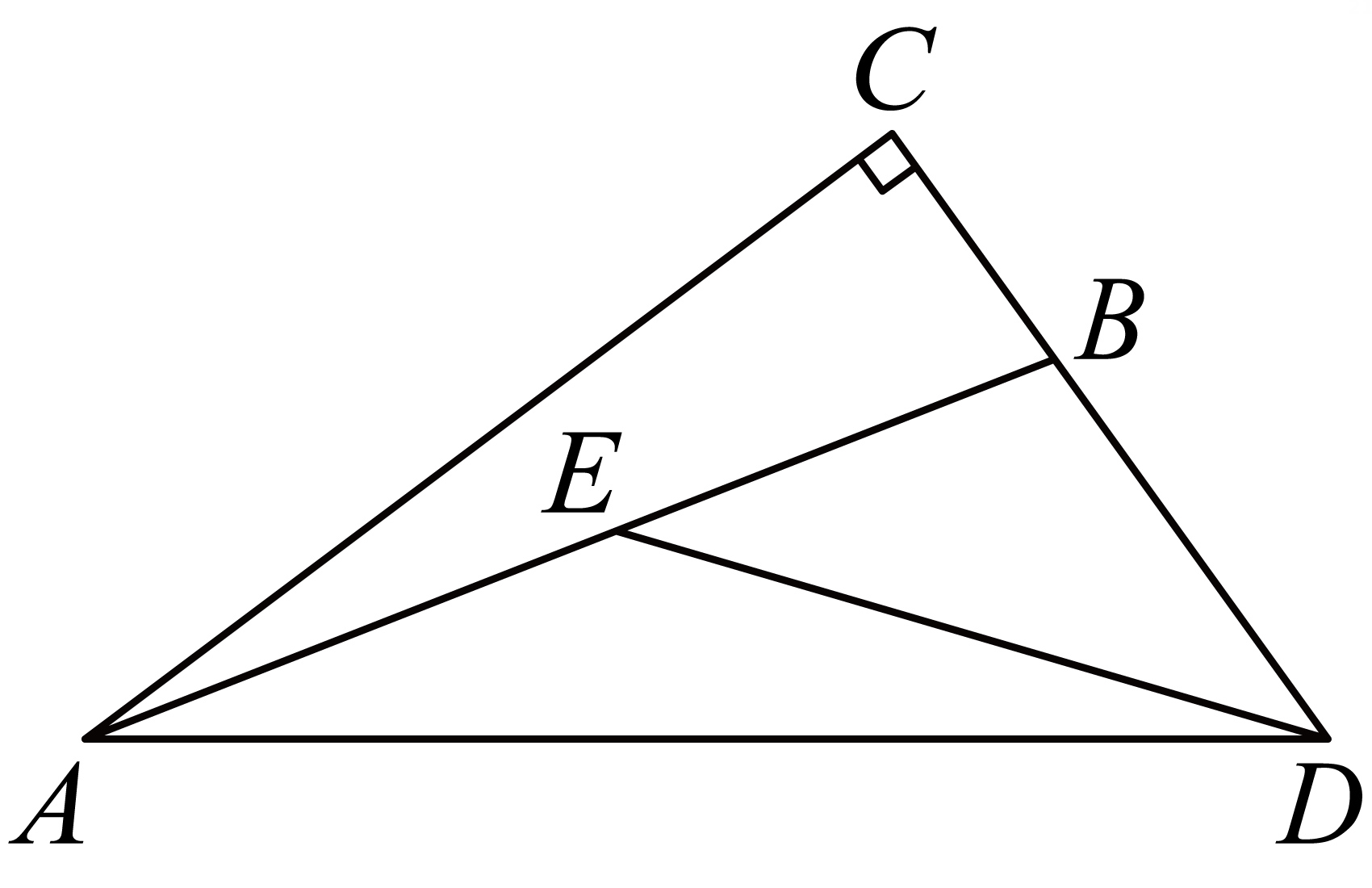(1)、若 $∠ B E D = 4 0^{°}$ ，求 $∠ B A D$ 的度数.

(2)、小真同学通过画图和测量得到以下近似数据：
AE
4cm
6cm
8cm
10cm
BC
2cm
3cm
4cm
5cm
猜想：AE与BC之间的等量关系，并给出证明.

(3)、探究 $A D, A B, B D$ 三者之间的等量关系，并给出证明.

查看试题解析
18. 如图，已知 $△ A B C$ 和 $△ A C D$ ， $∠ A B C = ∠ C A D = 90 °$ ， $A C = A D$ ， $A B > B C$ ，点 $C$ 关于直线 $A B$ 的对称点为 $C^{'}$ ，线段 $C^{'} D$ 交边 $A B$ 于点 $E$ ，交 $∠ C A D$ 的平分线于点 $F$ ，连接 $C F$ ．

(1)、求证： $C F = D F$ ；

(2)、求 $∠ A E F$ 的度数；

(3)、探究 $D E$ 与 $A B$ 的数量关系，并说明理由．

查看试题解析
19. 如图，在等边 $△ A B C$ 中，点 $D$ 是 $B C$ 边上一点（点 $D$ 不与端点重合）．作点 $D$ 关于直线 $A B$ 的对称点 $E$ ，连接 $A E$ ，在射线 $D A$ 上取一点 $F$ ，使 $∠ E F D = 60 °$ ， $E F$ 与 $A C$ 所在直线交于点 $G$ ．

(1)、求证： $∠ C A D = ∠ A H G$ ；

(2)、若 $A D = 2$ ，求 $E G$ 的长；

(3)、当 $D$ 在 $B C$ 边上运动时，判断 $△ A B C$ ， $△ A B D$ ， $△ A E G$ 面积之间的数量关系，并说明理由．

查看试题解析
20. 如图 $1$ ，在等边三角形 $A B C$ 的 $A C$ ， $B C$ 边上分别取点 $E$ ， $F$ ，使 $A E = C F$ ，连结 $B E$ ， $A F$ 相交于点 $P$ ．

(1)、求 $∠ B P F$ 的度数．

(2)、若 $∠ C B E = 45 °$ ， $P F = 2$ ，求 $B F$ 的长．

(3)、如图 $2$ ，连结 $C P$ ，若 $∠ B P C = 90 °$ ， $A B = 7$ ，求 $B P$ 的长．

查看试题解析
21. 如图1， $△ A B C$ 和 $△ C D E$ 都是等腰直角三角形， $∠ A C B = ∠ D C E = 90 °$ ， $D$ 为 $△ A B C$ 外一点， $A B > 2 C D$ ，点 $A$ ， $C$ ， $E$ 三点不共线，连结 $A D$ ， $A E$ ， $B D$ ， $B E$ ， $A E$ 与 $B D$ 交于点 $F$ ．

(1)、求证： $A E = B D$ ；

(2)、当 $A D^{2} + 2 C D^{2} = B D^{2}$ 时，求 $∠ A D C$ 的度数；

(3)、如图 $2$ ，当 $B C ∥ D E$ 时， $C D = \sqrt{2}$ ， $A C = 3$ ，求四边形 $A B E D$ 的面积．

查看试题解析
22. 如图，在 Rt $△ A B C$ 和 Rt $△ D E C$ 中， $∠ A C B = ∠ C D E = 90^{\circ}$ ，点 $A$ 在 $C E$ 上， $B A$ 的延长线恰好经过点 $D, A E = D E$ ．

(1)、若 $∠ B = 30^{\circ}$ ，判断 $△ A D E$ 的形状并说明理由；

(2)、已知 $A C = 5$ ，设 $D E = x, B C^{2} = y$ ．
①求 $y$ 关于 $x$ 的函数关系式；②若 $A B - A D = 6$ ，求线段 $A E$ 的长．

查看试题解析
23. 如图1，ΔABC和ΔCDE都是等腰直角三角形，∠ACB=∠DCE=90°，D为ΔABC外一点，AB>2CD，A，C，E三点不共线，连结AD，AE，BD，BE，AE与BD交于点F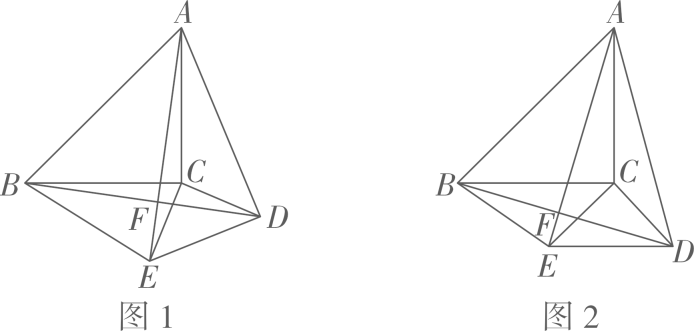

(1)、求证：AE=BD；

(2)、当AD²+2CD²=BD²时，求∠ADC的度数；

(3)、如图2，当BC∥DE时，CD= $\sqrt{2}$ ， AC=3，求四边形△BED的面积.

查看试题解析
24. 综合与实践
【建立模型】
（1）如图（1）， $△ A B C$ 为等边三角形，点D在 $B C$ 的延长线上，在 $B D$ 的同侧以 $C D$ 为边构造等边三角形 $C D E$ ，连接 $B E$ ， $A D$ 交于点F．
求证： $B E = A D$ ，并直接写出 $∠ A F B$ 的度数．
【应用模型】
（2）①如图（2），在 $△ A B C$ 中， $A D$ 平分 $∠ B A C$ ，且 $A D = A C$ ，点E在 $A D$ 的延长线上，且 $A B = A E$ ，连接 $B E$ ， $C E$ ，求证： $B E = C E$ ．
②如图（3）， $△ A B C$ 和 $△ A D E$ 都是等腰三角形， $∠ B A C = ∠ D A E = 90 °$ ，点C恰好在 $E D$ 延长线上，连接 $B D$ ，若 $A B = 4$ ， $A E = 2$ ，求 $△ B D C$ 的面积．

查看试题解析

AE	4cm	6cm	8cm	10cm
BC	2cm	3cm	4cm	5cm