3.3 探索与表达规律培优课时卷-北师大版数学七年级上册

试卷更新日期：2025-12-10 类型：同步测试

进入出卷网下载

一、选择题

1. 已知正六边形ABCDEF (每条边都相等)在数轴上的位置如图所示，点A，F对应的数分别为-2和-1，现将正六边形ABCDEF绕着顶点按顺时针方向在数轴上连续翻转，翻转1次后，点E 所对应的数为0.连续翻转2000次后，在数轴上1998这个数对应( )

A、点A B、点D C、点E D、点F

查看试题解析
2. 根据图中数字的排列规律，在第⑩个图中， $a - b - c$ 的值是（）

A、 $- 512$ B、 $- 514$ C、510 D、512

查看试题解析
3. 如图，某点从数轴上的A点出发，第1次向右移动1个单位长度至B点，第2次从B点向左移动2个单位长度至C点，第3次从C点向右移动3个单位长度至D点，第4次从D点向左移动4个单位长度至E点，依此类推，经过n次移动后该点到原点的距离为50个单位长度，则符合条件的n的和为（）

A、205 B、202 C、199 D、196

查看试题解析
4. 已知 $a_{1} = 3 ， a_{2} = \frac{1}{1 - a_{1}} ， a_{3} = \frac{1}{1 - a_{2}} ， a_{4} = \frac{1}{1 - a_{3}} ， \cdot \cdot \cdot$ ，依此类推，则 $a_{2024}$ 等于（）．

A、 $- \frac{1}{2}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、3

查看试题解析
5. 如图，点O在直线AB上，点 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ， …，在射线OA上，点 $B_{1}$ ， $B_{2}$ ， $B_{3}$ ， …在射线OB上，图中相邻的点之间的距离为1．一个动点M从O点出发，以每秒1个单位长度的速度，按如图所示的箭头方向，沿着实线段和以点O为圆心的半圆匀速运动，即从 $O \to A_{1} \to B_{1} \to B_{2} \to A_{2} \to A_{3} \to B_{3} \to B_{4} ⋯$ ，按此规律，则动点M到达 $A_{10}$ 点处所需时间为（）秒．

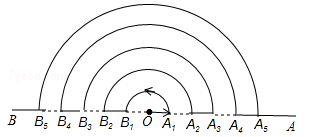A、10+55π B、20+55π C、10+110π D、20+110π

查看试题解析

6. 如图是节选课本110页上的阅读材料，请根据材料提供的方法求和：

\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \cdot \cdot \cdot + \frac{1}{2020 \times 2021}

，它的值是（）

上题是利用一系列等式相加消去项达到求和，这种方法不仅限于整数求和，如

$1 - \frac{1}{2} = \frac{1}{1 \times 2}$ ① $\frac{1}{2} - \frac{1}{3} = \frac{1}{2 \times 3}$ ② $\frac{1}{3} - \frac{1}{4} = \frac{1}{3 \times 4}$ ③ $\frac{1}{4} - \frac{1}{5} = \frac{1}{4 \times 5}$ ④ ……

继续写出上述第n个算式，并把这些算式两边分别相加，会得到： $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \cdot \cdot \cdot + \frac{1}{n \times (n + 1)}$ ．

A、1 B、

\frac{2020}{2021}

C、

\frac{2019}{2020}

D、

\frac{1}{2021}

查看试题解析

7. 如图所示的是中国南宋数学家杨辉在详解《九章算法》中出现的三角形状的数列，又称为“杨辉三角形”该三角形中的数据排列有着一定的规律，若将其中 $-$ 组斜数列用字母 $a_{1}$ 、 $a_{2}$ ， $a_{3}$ ， $\dots$ 代替，如图 $2$ ，则 $a_{99} + a_{100}$ 的值为（）

A、9801 B、10000 C、10201 D、10500

查看试题解析

二、填空题

8. x，y，z都是有理数，且xyz<0，x+y+z>0.若 $a = - （ \frac{x}{∣ x ∣} +$ $\frac{y}{∣ y ∣} + \frac{z}{∣ z ∣}$ ），则 $a + a^{2} + a^{3} + \dots + a^{1001} =$ .

查看试题解析
9. 十九世纪的时候，MorizStern（1858）与AchilleBrocot（1860）发明了“一棵树”，称之为有理数树，它将全体正整数和正分数按照如图所示的方法排列．从1开始，一层一层的“生长”出来： $\frac{1}{1}$ 是第一层，第二层是 $\frac{2}{1}$ 和 $\frac{1}{2}$ ，第三层是 $\frac{3}{1}$ ， $\frac{2}{3}$ ， $\frac{3}{2}$ ， $\frac{1}{3}$ ， ……，按照这个规律， $\frac{28}{13}$ 在第层第个数（从左往右数）．

查看试题解析
10. 在计算两位数的平方运算时，我们可以利用“竖式”方式进行快速运算，其步骤如图所示（图1，2，3），现有一个两位数，其十位数字为 $x$ ，在进行平方运算时，部分步骤如图4所示（ $x$ 为小于 $5$ 的正整数），则这个两位数是（用含 $x$ 的代数式表达）．

查看试题解析
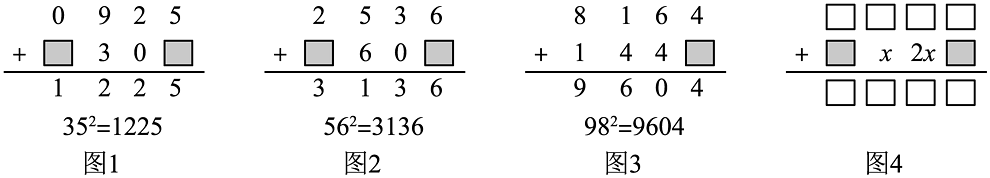11. 已知n个数x₁ ， x₂ ， …， xn，每个数只能取0，1，-1中的一个.若 $x_{1} + x_{2} + \dots + x_{n} = 2016,$ 则 $x_{1}^{2017} + x_{2}^{2017} + \dots + x_{n}^{2017}$ 的值为.

查看试题解析
12. 如图，定义一种对正整数n的 “ $F$ ” 运算：①当n为奇数时， $F_{n} = 3 \times n + 1$ ；②当n为偶数时， $F_{(n)} = \frac{n}{2^{k}}$ （其中k是使 $F_{(n)}$ 为奇数的正整数）。两种运算交替重复进行。例如，取 $n = 24$ ，则有如图所示的运算：

若 $n =$ 5，则第2025次“ $F$ ” 运算的结果是．

查看试题解析

三、解答题

13. 研究下列式子，你能发现什么规律？
第1个式子： $(x - 1) (x + 1) = x^{2} - 1$ ；第2个式子： $(x - 1) (x^{2} + x + 1) = x^{3} - 1$ ；第3个式子： $(x - 1) (x^{3} + x^{2} + x + 1) = x^{4} - 1$ ；…

(1)、第4个式子是；

(2)、请用含 $n (n$ 为正整数 $)$ 的式子表示你发现的规律；

(3)、请用你所发现的规律进行计算： $2^{20} - 2^{19} + 2^{18} - 2^{17} + \dots - 2^{3} + 2^{2} - 2 + 1$ .

查看试题解析
14. 观察下面的点阵图和相应的等式，探究其中的规律：

(1)、认真观察，并在 $④$ 后面的横线上写出相应的等式．

(2)、结合（1）观察下列点阵图，并在 $⑤$ 后面的横线上写出相应的等式．

(3)、通过猜想，写出（2）中与第 $n$ 个点阵相对应的等式．

查看试题解析
15. 设一列数 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ， …， $x_{2024}$ 中，对于 $1 \leq n \leq 2022$ ，均有 $x_{n} + x_{n + 1} + x_{n + 2} = s$ （s是常数），已知 $x_{1} = 3$ ， $x_{2} = 3 t + 1$ ， $x_{9} = 2 t$ ， $x_{99} = 3 - t$ ．

(1)、直接写出下列数中相等的数： $x_{1}$ ， $x_{2}$ ， $x_{3}$ ， $x_{4}$ ， $x_{5}$ ， $x_{6}$ ， $x_{7}$ ， $x_{8}$ ， $x_{9}$ ．

(2)、求出s和t的值．

(3)、计算： ${(x_{81})}^{3} + {(x_{2014})}^{3} + {(x_{2024})}^{3}$

查看试题解析
16. 看图填空：如图，把一个面积为1的正方形等分成两个面积为 $\frac{1}{2}$ 的长方形，接着把面积为 $\frac{1}{2}$ 的长方形等分成两个面积为 $\frac{1}{4}$ 的长方形，再把面积为 $\frac{1}{4}$ 的长方形等分成面积为 $\frac{1}{8}$ 的长方形，如此进行下去……

(1)、试利用图形揭示的规律计算： $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} + \frac{1}{128} + \frac{1}{256} + \dots \frac{1}{2^{n}}$ ＝ ▲ ．
并使用代数方法证明你的结论．

(2)、请给利用图（2），再设计一个能求： $\frac{1}{2} + \frac{1}{2^{2}} + \frac{1}{2^{3}} + \frac{1}{2^{4}} + \dots + \frac{1}{2^{n}}$ 的值的几何图形．

查看试题解析
17. 大数学家高斯在上学读书时曾经研究过这样一个问题： $1 + 2 + 3 + \dots + n = ？$ 经过研究，这个问题的结论是 $1 + 2 + 3 + \dots + n = \frac{1}{2} n (n + 1)$ ，（n是正整数）．
现在我们来研究一个类似的问题：
$1 \times 2 + 2 \times 3 + \dots + n (n + 1) = ？$
观察下面三个特殊的等式，并且填空：
$1 \times 2 = \frac{1}{3} (1 \times 2 \times 3 - 0 \times 1 \times 2)$ ，
$2 \times 3 = \frac{1}{3} (2 \times 3 \times 4 - 1 \times 2 \times 3)$ ，
$3 \times 4 = \frac{1}{3} (3 \times 4 \times 5 - 2 \times 3 \times 4)$ ，
① $4 \times 5 = \frac{1}{3} \times$      ▲     ，…
将前两个等式的两边相加，可以得到 $1 \times 2 + 2 \times 3 = \frac{1}{3} \times 2 \times 3 \times 4$ ．
将三个等式的两边相加，可以得 $1 \times 2 + 2 \times 3 + 3 \times 4 = \frac{1}{3} \times 3 \times 4 \times 5$ ．
根据以上知识完成填空：
②计算： $1 \times 2 + 2 \times 3 + 3 \times 4 + 4 \times 5 = \frac{1}{3} \times$      ▲  ；
③计算： $1 \times 2 + 2 \times 3 + \dots + 10 \times 11 =$      ▲  ；
④计算： $1 \times 2 + 2 \times 3 + 3 \times 4 + \dots + n \times (n + 1) =$      ▲  ；
⑤依据上面的材料，试计算： $1 \times 2 \times 3 + 2 \times 3 \times 4 + 3 \times 4 \times 5 \dots + 10 \times 11 \times 12$ ；
⑥猜想： $1 \times 2 \times 3 + 2 \times 3 \times 4 + 3 \times 4 \times 5 \dots + n (n + 1) (n + 2) =$      ▲  ．

查看试题解析
18. 从2开始，连续的偶数相加，它们和的情况如表：
加数的个数n
     和为S
1
    $2 = 1 \times 2$
2
    $2 + 4 = 6 = 2 \times 3$
3
    $2 + 4 + 6 = 12 = 3 \times 4$
4
    $2 + 4 + 6 + 8 = 20 = 4 \times 5$
5
    $2 + 4 + 6 + 8 + 10 = 30 = 5 \times 6$

(1)、若 $n = 8$ 时，求S的值；

(2)、根据表中的规律猜想：用n的式子表示S的公式： $S = 2 + 4 + 6 + 8 + ⋯ + 2 n$ ；

(3)、根据上题的规律计算： $102 + 104 + 106 + ⋯ + 210 + 212$ 的值．

查看试题解析
19. 在生活中，密码的应用随处可见，密码学是一门既古老又新兴的学科，它主要研究如何安全地传递和存储保密信息．如图，现制定一种密码规则，这种规则在正整数和字母、字符之间建立了一种对应关系，其中正整数为密文，字母、字符为明文．例如，密文“2”翻译成明文为“C”，密文“258”翻译成明文为“CZ”．

(1)、明文“A”对应的密文为“”（写出符合条件的一种情况即可），密文“483847”翻译成明文为“”；

(2)、为了增加密码的破译难度，对于密文按如下规则又进行了再次加密，原密文记为“密文I”，再次加密的密文记为“密文Ⅱ”．
密文I： $t$
1
2
3
4
…
密文Ⅱ： $3 t + 4$
7
10
13
16
…
①若密文I中的正整数每增加1，则密文Ⅱ中正整数的变化规律为 ▲ ；
②若密文I中的“t”对应的明文与密文Ⅱ中的“3t+4”直接利用原规则对应的明文相同，求该明文．

查看试题解析

加数的个数n	和为S
1	$2 = 1 \times 2$
2	$2 + 4 = 6 = 2 \times 3$
3	$2 + 4 + 6 = 12 = 3 \times 4$
4	$2 + 4 + 6 + 8 = 20 = 4 \times 5$
5	$2 + 4 + 6 + 8 + 10 = 30 = 5 \times 6$

密文I： $t$	1	2	3	4	…
密文Ⅱ： $3 t + 4$	7	10	13	16	…