湘教版数学八年级上册5.2 勾股定理及逆定理第三课时同步分层练习

试卷更新日期：2025-12-08 类型：同步测试

进入出卷网下载

一、夯实基础

1. 如果三角形的三边分别为 $\sqrt{2}$ ， $\sqrt{6}$ ， $2$ ，那么这个三角形的形状为（　　）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形

查看试题解析
2. 在△ABC中，BC＝5，AC＝4，AB＝3，则（　　）

A、∠A＝90° B、∠B＝90° C、∠C＝90° D、无法确定

查看试题解析
3. 如果 $△ A B C$ 的三边分别为 $m^{2} - 1, 2 m, m^{2} + 1$ ，其中 $m$ 为大于1的正整数，则（）

A、 $△ A B C$ 是直角三角形，且斜边为 $m^{2} - 1$ B、 $△ A B C$ 是直角三角形，且斜边为2m C、 $△ A B C$ 是直角三角形，且斜边为 $m^{2} + 1$ D、 $△ A B C$ 不是直角三角形

查看试题解析
4. 如图，四边形 $A B C D$ 中， $∠ B = 90 °, A B = 9 m, B C = 12 m, C D = 8 m$ ， $A D = 17 m$ ，则四边形 $A B C D$ 的面积为（）

A、 $108 m^{2}$ B、 $114 m^{2}$ C、 $122 m^{2}$ D、 $158 m^{2}$

查看试题解析
5. 如果三角形中两边的平方和等于第三边的平方，那么这个三角形是，最大边所对的角是.

查看试题解析
6. 如图，在3×4的正方形网格中， $∠ 2 =$ $°$

查看试题解析
7. 已知 $△ A B C$ 中， $B C = a$ ， $A C = b$ ， $A B = c$ ，且满足 $|a - 5| + \sqrt{b - 12} + {(c - 13)}^{2} = 0$ ．则 $A B$ 边上的高为．

查看试题解析
8. 如图，在 $△ A B C$ 中，点 $D$ 是 $B C$ 边上一点，连接 $A D$ ．若 $A B = 10$ ， $A C = 17$ ， $B D = 6$ ， $A D = 8$ ，．

(1)、求 $∠ A D B$ 的度数；

(2)、求 $B C$ 的长．

查看试题解析

二、能力提升

9. 五根小木棒的长度分别为7，15，20，24，25，现将它们摆成两个直角三角形，摆放正确的是（）

A、 B、 C、 D、

查看试题解析
10. 下列条件：① $b^{2} = c^{2} - a^{2}$ ；② $∠ C = ∠ A - ∠ B$ ；③ $a ： b ： c = \frac{1}{3} ： \frac{1}{4} ： \frac{1}{5}$ ；④ $∠ A ： ∠ B ： ∠ C = 3 ： 4 ： 5$ ，能判定 $△ A B C$ 是直角三角形的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
11. 如图，三个正方形的面积分别为 $S_{1}$ ， $S_{2}$ ， $S_{3}$ ，且K是 $A B$ 中点．若 $S_{1} = 18$ ， $S_{2} = 7$ ， $S_{3} = 25$ ，则 $C K$ 的长为（）

A、 $\frac{5}{2}$ B、 $\sqrt{7}$ C、 $\frac{7}{2}$ D、5

查看试题解析
12. $△ A B C$ 的三边满足 $| a + b - 16 | + \sqrt{a - b - 4} + {(c - 8)}^{2} = 0$ ，则 $△ A B C$ 为（）

A、直角三角形 B、等腰三角形 C、等边三角形 D、等腰直角三角形

查看试题解析
13. 若△ABC的三边长满足. $A B : B C : A C = \sqrt{2} : 2 : \sqrt{2},$ ，则该三角形是三角形.

查看试题解析
14. 如图所示，已知 $A D = C D = 2 \sqrt{10}$ ， $B D = 2$ ， $B C = 3 B D$ ，则 $A B$ 的长为．

查看试题解析
15. 已知一个三角形的三条边的长分别为 $\sqrt{5}$ 、 $\sqrt{6}$ 和 $\sqrt{11}$ ，那么这个三角形的最大内角的大小为度．

查看试题解析
16. 如图，点P是在正 $△ A B C$ 内一点． $P A = 6$ ， $P B = 8$ ， $P C = 10$ ，将线段 $A P$ 绕点A逆时针旋转 $60 °$ 得到线段 $A P^{'}$ ，连接 $P^{'} P$ 、 $P^{'} C$ ，四边形 $A P C P^{'}$ 的面积为．

查看试题解析
17. 数学课上老师拿了一张如图所示的等腰三角形纸片 $A B C$ ，已知底边 $B C = 20 cm$ ，点D是腰 $A B$ 上一点，且 $C D = 16 cm$ ， $B D = 12 cm$ ．

(1)、请你判断 $△ B C D$ 的形状，并说明理由：

(2)、求三角形腰 $A B$ 的长度．

查看试题解析
18. 如图，有一块凹四边形的绿地 $A B C D$ ， $A D = 4 m$ ， $C D = 3 m$ ， $∠ A D C = 90 °$ ， $A B = 13 m$ ， $B C = 12 m$ ，求这块绿地 $A B C D$ 的面积．

查看试题解析

三、拓展创新

19. 为了测量如图墙体是否与地面垂直，即

M O

是否垂直

P N

于点

O

，在没有角尺、量角器、刻度尺，只有足够长、足够多的若干条无弹性的绳子的情况下，三个数学兴趣小组分别设计了三种不同解决方案，其中第一、第二组的设计方案如下表．

问题	如何测量墙体是否与地面垂直？
工具	若干条无弹性的绳子
小组	第一小组	第二小组	第三小组
测量方案	模仿古埃及人用结绳的方法，在一条绳子上打 $13$ 个结，得到 $12$ 条线段，且用叠合法使得这 $12$ 条线段都相等，设每一条线段长为 $a$ ．如下图放置这总长是 $12 a$ 的绳子，使在 $O M$ 上的绳子 $O A = 4 a$ ，在 $O N$ 上的绳子 $O B = 3 a$ ，若 $A B = 5 a$ ，则 $A O ⊥ O B$ ，即 $M O ⊥ P N$ 于点 $O$ ，否则不垂直．	如图2，在射线 $O M$ ， $O N$ 上分别取点 $A$ ， $B$ ，放置绳子 $A B$ ，对折 $A B$ 得到相等的两段 $A C$ ， $B C$ ，放置绳子 $O C$ ，用叠合法比较 $O C$ 与 $B C$ 的长度，若 $O C = B C$ ，则墙体与地面垂直，即 $M O ⊥ P N$ 于点 $O$ ，否则不垂直．
测量示意图

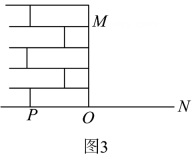(1)、第一、二小组的方案可行吗?如果可行，请分别给出证明；如果不可行，请说明理由．

(2)、请你代表第三小组，写出一个方案的应用原理不同于上述第一、第二小组的测量方案，并画出测量示意图，然后证明方案的可行性．

查看试题解析

湘教版数学八年级上册5.2 勾股定理及逆定理 第三课时 同步分层练习

一、夯实基础

二、能力提升

三、拓展创新

湘教版数学八年级上册5.2 勾股定理及逆定理第三课时同步分层练习