湘教版数学八年级上册 5.2 勾股定理及逆定理第二课时同步分层练习

试卷更新日期：2025-12-08 类型：同步测试

进入出卷网下载

一、夯实基础

1. 如图是一个无盖的长方体形盒子，长 $A B$ 为 $9 cm$ ，宽 $B C$ 为 $3 cm$ ，高 $C D$ 为 $5 cm$ ，点M在棱 $A B$ 上，并且 $A M = 3 cm$ ．一只蚂蚁在盒子内部，想从盒底的点M爬到盒顶的点D，则蚂蚁要爬行的最短路程是（） $cm$ ．

A、 $10 cm$ B、 $8 \sqrt{2} cm$ C、 $2 \sqrt{73} cm$ D、 $2 \sqrt{65} cm$

查看试题解析
2. 如图，一根垂直于地面的旗杆在离地面 $3 m$ 处撕裂折断，旗杆顶部落在离旗杆底部 $4 m$ 处，旗杯折断之前的高度是（）

A、 $5 m$ B、 $8 m$ C、 $10 m$ D、 $13 m$

查看试题解析
3. 如图，在 $Rt △ O A B$ 中， $O A = 2$ ， $A B = 1$ ， $O A$ 在数轴上，以原点 $O$ 为圆心，斜边 $O B$ 的长为半径画弧，交负半轴于一点，则这个点表示的实数是（）

A、 $\sqrt{5}$ B、 $- \sqrt{5}$ C、 $- 2$ D、2

查看试题解析
4. 如图，数轴上点 $C$ 所表示的数是（　　）

A、 $\sqrt{13}$ B、 $2 \sqrt{2}$ C、 $3.6$ D、 $3.7$

查看试题解析
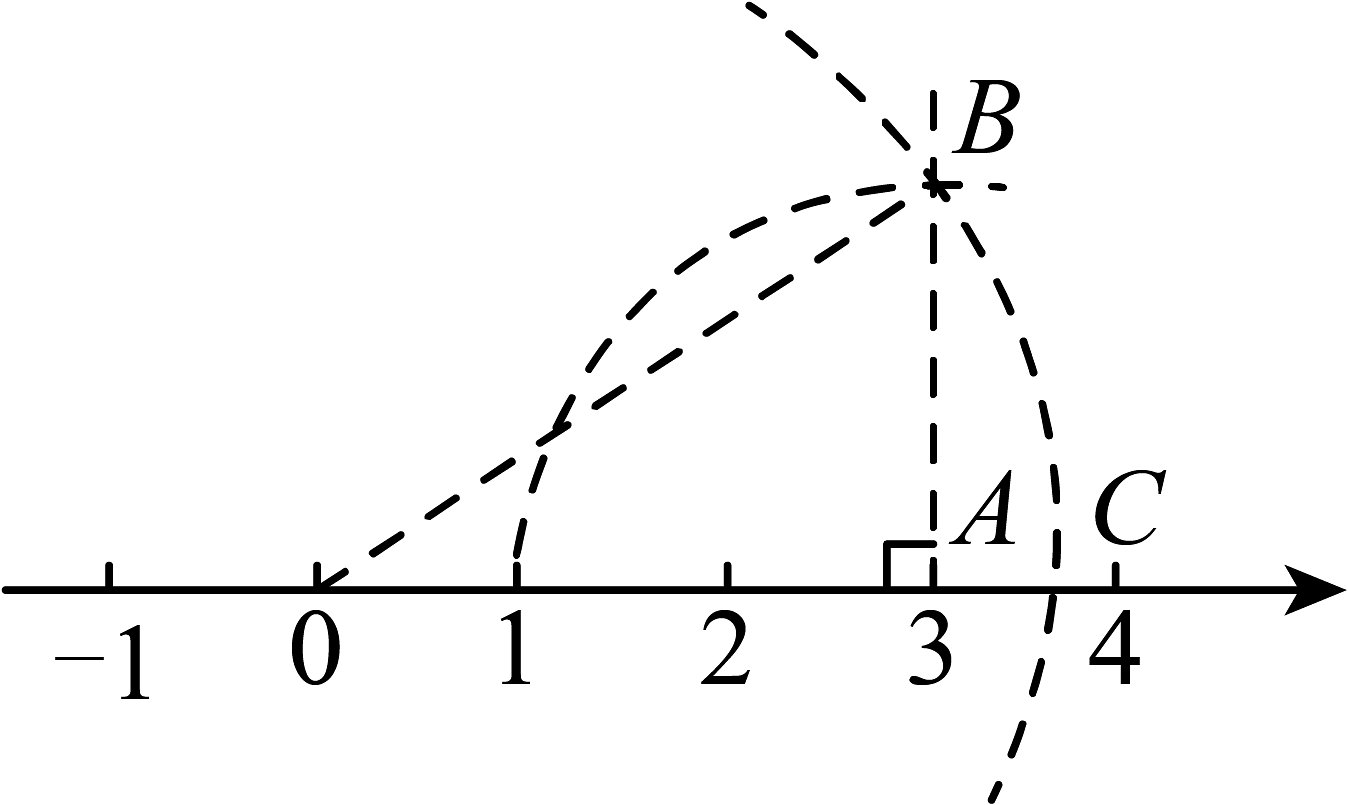5. 在我国古代数学著作《九章算术》中记载了一个有趣的问题，这个问题的意思是：如图，有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根新生的芦苇，它高出水面1尺．如果把这根芦苇沿与一边垂直的方向拉向岸边，那么它的顶端恰好到达岸边的水面，则水池的深度为（）

A、5尺 B、10尺 C、12尺 D、13尺

查看试题解析
6. 一架长 $5 m$ 的梯子，如图那样斜靠在一面墙上，梯子的底端离墙 $1.4 m$ ，如果梯子的顶端下滑 $0.8 m$ ，那么他的底部滑行了（）

A、 $0.8 m$ B、 $1 m$ C、 $1.2 m$ D、 $1.6 m$

查看试题解析
7. 一艘帆船由于风向原因先向正东方向航行了 $24 km$ ，然后向正北方向航行了 $10 km$ ，这时他离出发点 $km$ ．

查看试题解析
8. 如图，庭院中有两棵树，小鸟要从一棵高10m的树顶飞到一棵高4m的树顶上，两棵树相距8m，则小鸟至少要飞米．

查看试题解析
9. 如图，圆柱的底面周长是 $24 cm$ ，高是 $5 cm$ ，一只蚂蚁在 $A$ 点想吃到 $B$ 点的食物，需要爬行的最短路径是 $cm$ ．

查看试题解析
10. 如图，是一个三级台阶，它的每一级的长、宽，高分别为 $20 d m$ ， $3 d m$ 、 $2 d m$ ， $A$ 和 $B$ 是这个台阶两个相对的端点， $A$ 点有一只蚂蚁，想到 $B$ 点去吃可口的食物，则蚂蚁沿着台阶面爬到 $B$ 点的最短路程是 $d m$ 。

查看试题解析
11. 请解决我国古代数学著作《九章算术》中的一个问题：一根竹子原来高9尺，从 $A$ 处折断，折断后竹子顶端 $B$ 点落在离竹子底端 $O$ 点3尺处，求折断处离地面（即 $A O$ ）的高度是多少尺？

查看试题解析

二、能力提升

12. “赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为 a，较短直角边长为b，若 ${(a + b)}^{2} = 21$ ，大正方形的面积为13，则小正方形的面积为（）

A、 $6$ B、 $5$ C、 $8$ D、 $7$

查看试题解析
13. 如图，有一只摆钟，摆锤看作一个点，当摆锤静止时，它离底座的垂直高度 $D E = 6 cm$ ，当摆锤摆动到最高位置时，它离底座的垂直高度 $B F = 8 cm$ ，此时摆锤与静止位置时的水平距离 $B C = 10 cm$ 时，钟摆 $A D$ 的长度是（　　）

A、17 B、24 C、26 D、28

查看试题解析
14. 如图，有一个绳索拉直的木马秋千，绳索AB的长度为5米，若将它沿水平方向向前推进3米（即 $D E = 3$ 米），且绳索保持拉直的状态，则此时木马上升的高度为（）

A、1米 B、1.5米 C、2米 D、4米

查看试题解析
15. 如图是两人某次棋局棋盘上的一部分，若棋盘中每个小正方形的边长为1，则“车”、“炮”两棋子所在格点之间的距离为（）

A、 $\sqrt{5}$ B、3 C、 $\sqrt{10}$ D、 $4 \sqrt{10}$

查看试题解析
16. 如图，长方体的长为 $15 cm$ ，宽为 $10 cm$ ，高为 $20 cm$ ，点 $B$ 与点 $C$ 的距离为 $5 cm$ ，一只蚂蚁如果要沿着长方体的表面从点 $A$ 爬到点 $B$ 去吃一滴蜜糖，需要爬行的最短距离是（）

A、 $25 cm$ B、 $20 cm$ C、 $24 cm$ D、 $10 \sqrt{5} cm$

查看试题解析
17. 如图，网格中每个小方格的边长均为1，以数轴上表示数1的点为圆心，阴影正方形边长为半径画圆，交数轴于点 $P$ 和点 $Q$ ，则点 $Q$ 表示的数为．

查看试题解析

18. 明朝数学家程大位曾作词《西江月·秋千索长》．该诗词翻译后的示意图中，

O A

、

O B

表示秋千的绳索，

A C ⊥ O B

，

B C = 1

，

A C = 2

，则该秋千的索长

O A =

．

西江月·秋千索长

【明】程大位

平地秋千未起，踏板一尺离地．

送行二步与人齐，五尺人高曾记．

仕女佳人争蹴，终朝笑语欢嬉．

良工高士好奇，算出索长有几？

查看试题解析

19. 如图，数轴上有一个边长为 $1$ 的正方形 $A B C D$ ，其中点 $A$ 、 $B$ 表示的数分别为 $2$ 、 $3$ ，以 $B$ 为圆心，对角线 $B D$ 为半径画弧交数轴上点 $A$ 左边于点 $E$ ，则 $E$ 表示的数为．

查看试题解析
20. 在学校组织的研学活动中，需要学生自己搭建帐篷．下图是搭建帐篷的示意图．在 $△ A B C$ 中，支架 $A D$ 从帐篷顶点 $A$ 支撑在水平的支架 $B C$ 上，且 $A D ⊥ B C$ 于点 $D$ ，经测量得： $A B = 2 m$ ， $A D = 1.2 m$ ， $C D = 0.9 m$ ．按照要求，帐篷支架 $A B$ 与 $A C$ 所夹的角需为直角．请通过计算说明学生搭建的帐篷是否符合条件．

查看试题解析
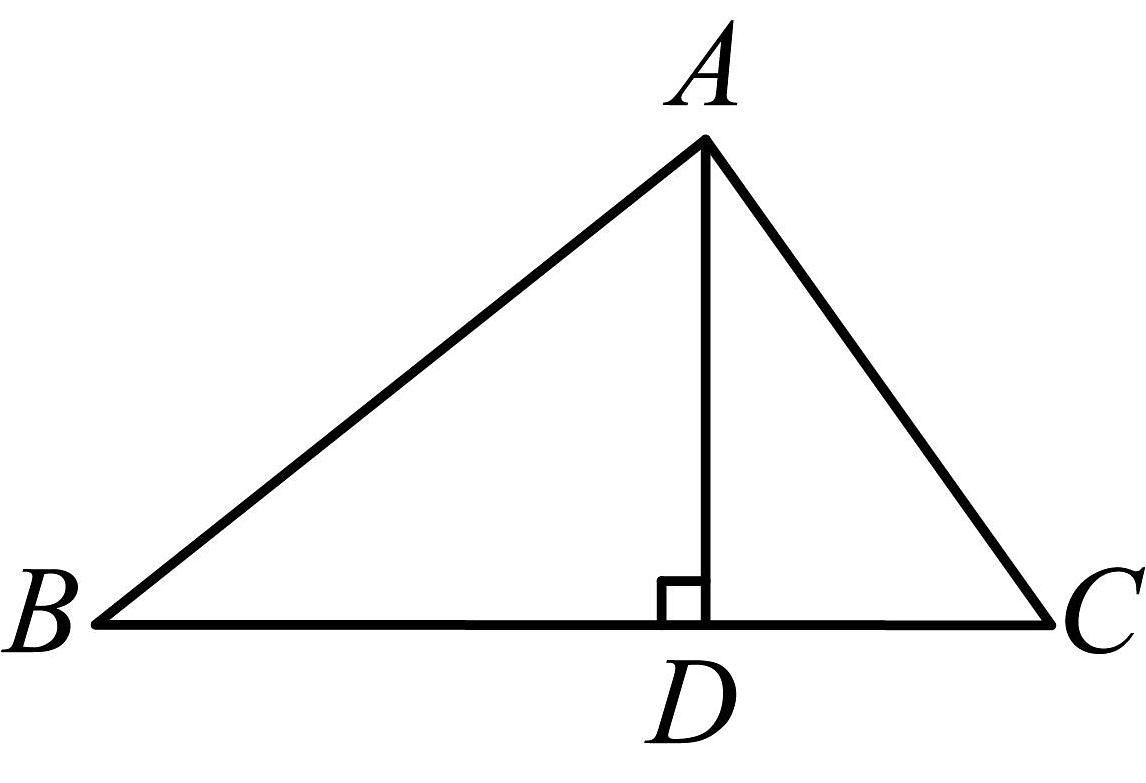21. 如图，某沿海城市 $A$ 接到台风预警，在该市正南方向 $340 km$ 的 $B$ 处有一台风中心，沿 $B C$ 方向以 $10 km/h$ 的速度移动，已知城市 $A$ 到 $B C$ 的距离 $A D$ 为 $160 km$ ．

(1)、台风中心经过多长时间从 $B$ 点移到 $D$ 点？

(2)、如果在距台风中心 $B$ 的 $200 km$ 的圆形区域内都将受到台风的影响，那么 $A$ 市受到台风影响的时间持续多少小时？

查看试题解析

三、拓展创新

22. 生活与应用

课题	小区遛狗捡球问题
生活情景	傍晚，子涵同学去小区遛狗，她观察发现，她站直身体时，牵绳的手离地面高度为 $A B = 1.7$ 米，小狗的高 $C D = 0.2$ 米，小狗与子涵的距离 $A C = 2$ 米．（绳子一直是直的）
情景示意图
问题1	（1）此时，牵狗绳 $B D$ 的长为______米；
问题2	（2）子涵将手上的小球扔至3米远的 $M$ 处（ $A M = 3$ 米），若她站着不动，将牵狗绳放长至4米，则小狗能否将小球捡回来？请说明理由．（假设小狗碰到球就能将球捡回来）

查看试题解析

23. 动手操作：
（1）如图1，把矩形 $A A^{'} B^{'} B$ 卷成以AB为高的圆柱形，则点A与点______重合，点B与点______重合；
探究与发现：
（2）如图2，若圆柱的底面周长是 $30 cm$ ，高是 $40 cm$ ，从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处作装饰，则这条丝线的最小长度是多少？
（3）如图3，在（2）的条件下，若用丝线从该圆柱的底部A缠绕4圈直到顶部B处，则至少需要多少丝线？

查看试题解析

湘教版数学八年级上册 5.2 勾股定理及逆定理 第二课时 同步分层练习

一、夯实基础

二、能力提升

三、拓展创新

湘教版数学八年级上册 5.2 勾股定理及逆定理第二课时同步分层练习