第一单元整式的乘除培优卷-北师大版数学七年级下册

试卷更新日期：2025-12-07 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共24分）

1. 已知 $a = 2^{12}$ ， $b = 3^{8}$ ， $c = 7^{4}$ ，则 $a$ ， $b$ ， $c$ 大小关系是（）

A、 $a > b > c$ B、 $b > a > c$ C、 $c > b > a$ D、 $b > c > a$

查看试题解析
2. “白色污染”的主要来源有食品包装袋、泡沫塑料填充物等．已知一个塑料快餐盒的污染面积为 $200 {cm}^{2}$ ，如果30万名游客每人丢弃一个快餐盒，那么造成污染的最大面积用科学记数法表示为（　　）

A、 $6 \times 10^{7} {cm}^{2}$ B、 $0.6 \times 10^{6} {cm}^{2}$ C、 $6 \times 10^{6} {cm}^{2}$ D、 $60 \times 10^{6} {cm}^{2}$

查看试题解析
3. 小明将 ${(2023 x + 2024)}^{2}$ 展开后得到 $a_{1} x^{2} + b_{1} x + c_{1}$ ；小亮将 ${(2024 x - 2023)}^{2}$ 展开后得到 $a_{2} x^{2} + b_{2} x + c_{2}$ ，若两人计算过程无误，则 $c_{1} - c_{2}$ 的值为（）

A、2023 B、2024 C、4047 D、1

查看试题解析
4. 设 $p = a^{2} + b^{2}$ ， $n = a b$ ，其中 $a = 2025 + t, b = 2023 + t$ ，给出以下结论：① $a - b = 2$ ；②当 $n = 4$ 时， $p = 12$ ；则下列判断正确的是（）

A、①，②都对 B、①，②都错 C、①对，②错 D、①错，②对

查看试题解析
5. 如图，正方形 ABCD 与正方形 CEFH 的面积和为 58，点 C 在线段 BE 上，点 H 在线段 CD 上，延长 FH 交 AB 于点 G. 若 $B E = 10$ ，则长方形 BCHG 的面积为（）

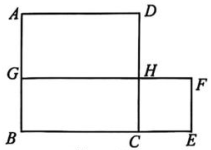A、21 B、24 C、34 D、42

查看试题解析
6. 已知 $(x + p) (x + q)$ 的乘积项中不含 $x$ 的一次项，则 $p$ 与 $q$ 的关系是（）

A、相等 B、互为相反数 C、互为倒数 D、乘积为-1

查看试题解析
7. 若A＝(2＋1)(2²＋1)(2⁴＋1)(2⁸＋1)＋1，则A的末位数字是（）

A、2 B、4 C、6 D、8

查看试题解析
8. 设 $m = a + b$ ， $n = a b$ ， $p = a^{2} + b^{2}$ ， $q = a^{2} - b^{2}$ ，其中 $a = 2023 + t$ ， $b = 2021 + t$ ，给出以下结论：① 当 $n = 4$ 时， $p = 12$ ；② 不论t为何值， $\frac{p}{q} = \frac{n + 2}{m}$ 。则下列判断正确的是（）

A、①， B、都对B.①，②都错 C、①对，②错 D、①错，②对

查看试题解析

二、填空题（每题3分，共15分）

9. 若 $2^{a} + 2^{a} + 2^{a} + 2^{a} = 2^{b} \times 2^{b} \times 2^{b} \times 2^{b}$ (a，b 是常数)，则 a，b 满足的关系式是.

查看试题解析
10. 如图，正方形 $A E H G$ ，正方形 $E B K F$ 和正方形 $N K C M$ 摆放在长方形 $A B C D$ 中， $A B = 3, B C = 4$ ，且 $B K > K C$ ．已知正方形 $A E H G$ 与正方形 $N K C M$ 的面积之和为7，则长方形 $P F Q D$ 的面积为．

查看试题解析
11. 若 $(x + 2) (x - 3) = 7$ ，则 $(x + 2)^{2} + (x - 3)^{2}$ 的值为

查看试题解析
12. $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) \dots (1 - \frac{1}{99^{2}}) (1 - \frac{1}{100^{2}})$ =；

查看试题解析
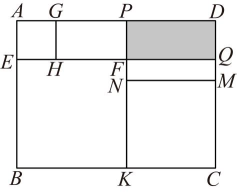13. 我国南宋数学家杨辉用 “三角形”解释二项和的乘方规律，称之为 “杨辉三角”，这个 “三角形” 给出了 $(a + b)^{n} (n = 1 ， 2 ， 3 ， 4 ， \dots)$ 的展开式的系数规律 (按 $n$ 的次数由大到小的顺序)．
请依据上述规律，写出 ${(x - \frac{1}{x})}^{2023}$ 展开式中含 $x^{2021}$ 项的系数是．

查看试题解析

三、解答题（共7题，共61分）

14. 定义一种幂的新运算：x^a⊕x^b=x^ab+x^a+b ，请利用这种运算规则解决下列问题.

(1)、求2²⊕2³的值；

(2)、2^P=3，2^q=5，3^q=6，求2^P⊕2^q的值；

(3)、若运算9⊕3^2t的结果为810，则t的值是多少?

查看试题解析
15. 数与形是数学研究的两大部分，它们间的联系称为数形结合，整式乘法中也可以利用图形面积来论证数量关系，现用砖块相同的面（如图1，长为a，宽为b的小长方形）拼出以下图形，延长部分边框，则把这些拼图置于如图所示的正方形或大长方形内，请解答下列问题.

(1)、图2中空白面积为 $S_{1}$ ，根据图形中的数量关系，用含a，b的式子表示 $S_{1}$ .

(2)、图2，图3中空白部分面积 $S_{1}$ ， $S_{2}$ 分别为19，68，求ab值.

查看试题解析
16. 已知有若干张正方形卡片和长方形卡片，其中 $A$ 型卡片是边长为 $a$ 的正方形， $B$ 型卡片是边长为 $b$ 的正方形， $C$ 型卡片是长为 $a$ ，宽为 $b$ 的长方形，

(1)、若要用这三种卡片紧密拼接成一个长为 $(3 a + b)$ ，宽为 $(a + 2 b)$ 的长方形，求需要 $A, B, C$ 各型号卡片各多少张?

(2)、若要用这三种卡片紧密拼接成一个正方形，先取 $A$ 型卡片9张，再取 $B$ 型卡片4张，还需 $C$ 型卡片张.

(3)、用一张 $A$ 型卡片，一张 $B$ 型卡片，一张 $C$ 型卡片紧密拼接成如下图所示的图形，若阴影部分的面积为 $32, C$ 型卡片的面积为48，求 $a, b$ 的值.

查看试题解析
17. 观察：
$2^{2} - 1^{2} = (2 + 1) \times (2 - 1) = 2 + 1 = \frac{(1 + 2) \times 2}{2} = 3$ ；
$4^{2} - 3^{2} + 2^{2} - 1^{2} = (4 + 3) \times (4 - 3) + (2 + 1) \times (2 - 1) = 4 + 3 + 2 + 1 = \frac{(1 + 4) \times 4}{2} = 10$ ；
……
探究：

(1)、通过观察发现，材料中的计算过程逆用了平方差公式，即： $a^{2} - b^{2} =$ ________；

(2)、请用上述方法，求 $8^{2} - 7^{2} + 6^{2} - 5^{2} + 4^{2} - 3^{2} + 2^{2} - 1^{2}$ 的值；
应用：

(3)、如图，100个圆由小到大套在一起，从外向里相间画阴影，最外面一层画阴影，最外面的圆的半径为 $100 cm$ ，向里依次为 $99 cm$ ， $98 cm$ ， ⋯⋯， $1 cm$ ，那么在这个图形中，所有阴影的面积和是多少？（结果保留 $π$ ）

查看试题解析
18. 观察下列各式：
(x-1)(x+1)=x²-1；
(x-1)(x²+x+1)=x³-1；
(x-1)(x³+x²+x+1)=x⁴-1；
……

(1)、根据规律可得(x- 1)(x^n-1+……+x+1)= (其中n为正整数)．

(2)、计算：(3-1)(3⁵⁰ +3⁴⁹+3⁴⁸+……+3²+3+1)．

(3)、计算：(-2)¹⁹⁹⁹+(-2)¹⁹⁹⁸+(-2)¹⁹⁹⁷ +……+(-2)³+(-2)²+(-2)+1．

查看试题解析
19. 【知识生成】用两种不同方法计算同一图形的面积，可以得到一个等式，如图①，是用长为 $2 a$ ，宽为 $2 b$ 的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按照图②拼成一个正方形，可以得到 ${(a - b)}^{2}$ 、 ${(a + b)}^{2}$ 、 $a b$ 三者之间的等量关系式：
【知识迁移】类似地，用两种不同的方法计算同一个几何体的体积，也可以得到一个等式，如图3，观察大正方体分割，可以得到等式：
【成果运用】利用上面所得的结论解答：
（1）已知 $a + b = 7$ ， $a b = \frac{13}{4}$ ，求 $a - b$ 的值；
（2）已知 $|a + b - 6| + {(a b - 7)}^{2} = 0$ ，求 $a^{3} + b^{3}$ 的值．

查看试题解析
20. 类比是数学中常用的数学思想．比如，我们可以类比多位数的加、减、乘、除的竖式运算方法，得到多项式与多项式的加、减、乘、除的运算方法．例：
① $\begin{array}{l} \begin{array}{l} 2 x + 3 \end{array} \\ \frac{\begin{array}{l} +) & 3 x - 5 \end{array}}{\begin{array}{l} 5 x - 2 \end{array}} \end{array}$     ② $\begin{array}{l} \begin{array}{l} 3 x^{2} - 4 x + 1 \end{array} \\ \frac{\begin{array}{l} -) & x^{2} + 0 - 5 \end{array}}{\begin{array}{l} 2 x^{2} - 4 x + 6 \end{array}} \end{array}$
$∴ (2 x + 3) + (3 x - 5) = 5 x - 2$          $∴ (3 x^{2} - 4 x + 1) - (x^{2} - 5) = 2 x^{2} - 4 x + 6$
③ $\begin{array}{l} \begin{array}{l} x & + & 3 \end{array} \\ \frac{\begin{array}{l} \times) & 2 x & + & 5 \end{array}}{\begin{array}{l} 5 x & + & 15 \end{array}} \\ \frac{\begin{array}{l} 2 x^{2} & + & 6 x \end{array}}{\begin{array}{l} 2 x^{2} & + & 11 x & + & 15 \end{array}} \end{array}$              ④ $x - 3 \begin{matrix} 2 x + 3 \\ \begin{array}{l} 2 x^{2} - 3 x - 9 \\ \frac{2 x^{2} - 6 x}{3 x - 9} \\ \frac{3 x - 9}{0} \end{array} \end{matrix}$
$∴ (x + 3) (2 x + 5) = 2 x^{2} + 11 x + 15$       $∴ (2 x^{2} - 3 x - 9) \div (x - 3) = 2 x + 3$
理解应用：

(1)、请仿照上面的竖式计算： $(2 x + 3) (x - 5)$ ；

(2)、已知两个多项式的和为 $3 x^{2} - \frac{7}{2} x + 5$ ，其中一个多项式为 $x^{2} - 2$ ，请用竖式的方法求出另一个多项式．

(3)、已知一个长为 $(x + 2)$ ，宽为 $(x - 2)$ 的矩形 $A$ ，将它的长增加8，宽增加 $a$ 得到一个新矩形 $B$ ，且矩形 $B$ 的周长是矩形 $A$ 周长的3倍（如图），求矩形 $B$ 的面积．

查看试题解析

第一单元 整式的乘除 培优卷-北师大版数学七年级下册

一、单选题（每题3分，共24分）

二、填空题（每题3分，共15分）

三、解答题（共7题，共61分）

第一单元整式的乘除培优卷-北师大版数学七年级下册