第一单元整式的乘除提升卷-北师大版数学七年级下册

试卷更新日期：2025-12-07 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共24分）

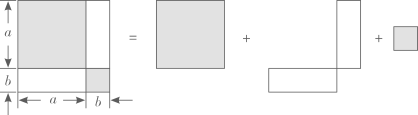
1. 下列运算中，正确的是（）

A、 ${(a b^{2})}^{3} = a b^{6}$ B、 ${(3 c d)}^{3} = 9 c^{3} d^{3}$ C、 ${(- 2 a^{3} b)}^{2} = 4 a^{6} b^{2}$ D、 ${(- 3 a^{3})}^{2} = 9 a^{5}$

查看试题解析
2. 截至2025年3月31日，中国半导体产业实现重大突破，验证了自主研发的多重曝光技术具备0.000000005米（5纳米）芯片的生产能力，数0.000000005用科学记数法表示为（）

A、 $5 \times 1 0^{- 9}$ B、 $5 \times 1 0^{- 8}$ C、 $0.5 \times 1 0^{- 9}$ D、 $0.5 \times 1 0^{- 8}$

查看试题解析
3. 若 $(x^{2} - m x + 1) (x - 3)$ 展开后不含 $x^{2}$ 的项，则m的值是（）

A、 $- \frac{1}{3}$ B、1 C、3 D、 $- 3$

查看试题解析
4. 如图是利用割补法求图形面积的示意图，下列公式中与之相对应的是（）

A、 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ B、 $(a - b)^{2} = a^{2} - 2 a b + b^{2}$ C、 $(a + b) (a - b) = a^{2} - b^{2}$ D、 $(a b)^{2} = a^{2} b^{2}$

查看试题解析
5. 小明将 ${(2023 x + 2024)}^{2}$ 展开后得到 $a_{1} x^{2} + b_{1} x + c_{1}$ ；小亮将 ${(2024 x - 2023)}^{2}$ 展开后得到 $a_{2} x^{2} + b_{2} x + c_{2}$ ，若两人计算过程无误，则 $c_{1} - c_{2}$ 的值为（）

A、2023 B、2024 C、4047 D、1

查看试题解析
6. 如图可以通过不同的方法计算图形的面积，可以得到一个数学等式，这个大正方形边长为α+b+c，用（a+b+c）²可求得其面积。同时，大正方形的面积也等于6个长方形和3个正方形的面积之和；已知a+b+c=8，a²+b²+c²=26，则ab +bc+ac的值是（）

A、34 B、23 C、20 D、19

查看试题解析
7. 如果 $x = 2^{m} + 1, y = 2 + 4^{m}$ （ $m$ 为整数），那么用含 $x$ 的代数式表示 $y$ 为（）

A、 $y = 2 x$ B、 $y = x^{2}$ C、 $y = (x - 1)^{2} + 2$ D、 $y = x^{2} + 1$

查看试题解析
8. 若 $x^{2} - k x - 24 = (a x + 12) (x - 2)$ ，则 $k$ 的值是（）

A、10 B、-10 C、 $\pm 10$ D、14

查看试题解析

二、填空题（每题3分，共15分）

9. 计算： ${(\frac{3}{2})}^{2025} \times {(- \frac{2}{3})}^{2026}$ 的结果是．

查看试题解析
10. 已知 $a + b = 4$ ， $a^{2} - b^{2} = 12$ ，则 $a - b =$ ．

查看试题解析
11. 若 $n$ 满足 ${(n - 2024)}^{2} + {(2025 - n)}^{2} = 7$ ，则 $(2025 - n) (n - 2024) =$ ．

查看试题解析
12. 如图，已知正方形ABCD和BEFG，点A，B，E三点共线，AE=12.8，CG=5，则△ABD与△BEF的面积差是.

查看试题解析
13. 有两张正方形纸片 $A B C D 、 E F G H$ ，其中 $A B > E F$ ．若将这两个正方形纸片按图（1）所示的方式放置（点B和点F重合），产生了一个新的、周长为8的正方形 $M H N D$ ．若将这两个正方形纸片按图（2）所示并排放置，其中，点B和点E重合，点A ， B ， F在同一条直线上，点P是线段 $A F$ 的中点．连接 $A H ， P D ， P G$ ，若三角形 $A B H$ 的面积是3．则图（2）中阴影部分的面积是．

查看试题解析

三、解答题（共7题，共61分）

14. 已知 $x_{}^{2} + y_{}^{2} = 9$ ， $x + y = 4$ ，求下列代数式的值：

(1)、 $x y$ ；

(2)、 $(x - 3) (y - 3)$ ．

查看试题解析
15. 先化简，再求值： $[(x + 4 y) (x - 4 y) - {(x - 3 y)}^{2} - 3 x y] \div (3 y)$ ，其中 $x = - \frac{1}{3} ， y = - 1$ ．

查看试题解析
16. 一个长方体模型的长、宽、高分别为4a(cm)，3a(cm)，2a(cm)。某种油漆每千克可漆面积为 $\frac{1}{2} a (c m^{2}),$ ，问：漆这个模型需要油漆多少千克?

查看试题解析
17. 在数学中．我们经常会运用逆向思考的方法来解决一些问题．

(1)、已知 $a^{m} \div a^{n} = a^{m - n}$ ，若 $a^{m} = 4$ ， $a^{m - n} = 2$ ，请你也利用逆向思考的方法求 $a^{n}$ 的值；

(2)、下面是小贤用逆向思考的方法完成的一道作业题．请你参考小贤的方法解答问题：
小贤的作业
计算： $8^{9} \times {(- 0.125)}^{9}$ ．
解： $8^{9} \times {(- 0.125)}^{9} = {(- 8 \times 0.125)}^{9} = {(- 1)}^{9} = - 1$ ．
计算： $5^{2025} \times {(- 0.2)}^{2024}$ ．

查看试题解析
18. 小聪在学习完乘法公式后，发现完全平方公式通过代数变形，可以解决很多数学问题，例如：已知 $a + b = 7$ ， $a b = 4$ ，求 $a^{2} + b^{2}$ 的值．答案解： $∵ a + b = 7$ ； $∴ {(a + b)}^{2} = 7^{2} = 49$ ； $∴ a^{2} + b^{2} = {(a + b)}^{2} - 2 a b = 41$ 根据上面的解题思路与方法，解决下列问题：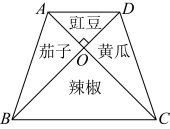

(1)、已知 $a - b = 4$ ， $a b = 3$ ，求 ${(a + b)}^{2}$ 的值；

(2)、为贯彻《关于全面加强新时代大中小学劳动教育的意见》的方针政策，帮助同学们更好地理解劳动的价值与意义，培养学生的劳动情感、劳动能力和劳动品质，天府新区某校开垦了如图所示的一块梯形空地 $A B C D$ 作为劳动实践基地，并分成四块．其中， $A C ⊥ B D$ 于点O ， $O A = O D, O B = O C$ ．计划在 $△ A O B$ 和 $△ C O D$ 区域内组织同学们种茄子和黄瓜，在 $△ A O D$ 和 $△ B O C$ 的区域内种豇豆和辣椒，经测量，种豇豆和辣椒区域的面积和为 $84.5$ 平方米， $A C = 17$ 米，求种茄子和黄瓜区域的面积和是多少平方米．

查看试题解析
19. 若一个正整数m是两个连续正奇数的乘积，即 $m = n (n + 2)$ ，其中n为正奇数，则称m为“相邻奇数积”，n为m的“较小奇因数”．例如， $35 = 5 \times 7$ ，则35是“相邻奇数积”，5为35的“较小奇因数”．

(1)、a是“相邻奇数积”，它的“较小奇因数”为3，则 $a =$ ；b是63的“较小奇因数”，则 $b =$ ．

(2)、求证：“相邻奇数积”比构成它的两个奇因数的和的一半的平方小1．

(3)、若x，y均为“相邻奇数积”，且它们的较小奇因数是两个连续奇数，设 $p = x - y$ ，若正数p是一个两位数，求x的最大值．

查看试题解析
20. 【实践探究】如图①，在边长为 $a$ 的大正方形中剪去一个边长为 $b$ 的小正方形（ $a > b$ ），把图①中 $L$ 形的纸片按图②分成I、II、III、IV四个部分，并剪拼成如图③的一个大长方形；

(1)、请写出从图①到图③验证的乘法公式为： ▲ ，并说明理由．

(2)、【应用探究】利用（1）中验证的公式简便计算： $499 \times 501 + 1$ ；

(3)、【知识迁移】类似地，我们还可以通过对立体图形进行变换得到代数恒等式．如图④，在一个棱长为 $a$ 的正方体中去掉一个棱长为 $b$ 的正方体，再把剩余立体图形切割分成如图⑤的三部分，利用立体图形的体积，可得恒等式为： $a^{3} - b^{3} =$ ▲ ．（结果不需要化简）

查看试题解析

第一单元 整式的乘除 提升卷-北师大版数学七年级下册

一、选择题（每题3分，共24分）

二、填空题（每题3分，共15分）

三、解答题（共7题，共61分）

第一单元整式的乘除提升卷-北师大版数学七年级下册