北师大版数八年级上册单元分层检测卷-第七章《命题与证明》B卷

试卷更新日期：2025-12-07 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 如图，两条平行线a、b被第三条直线c所截．若∠1＝70°，则∠2＝（　　）

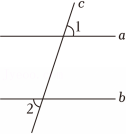A、130° B、110° C、90° D、70°

查看试题解析
2. 如图，两个平面镜平行放置，光线经过平面镜反射时， $∠ 1 = ∠ 2 = 40 °$ ，则 $∠ 3$ 的度数为（）

A、 $80 °$ B、 $90 °$ C、 $100 °$ D、 $120 °$

查看试题解析
3. 如图，已知直线 $l_{1} ∥ l_{2}$ ， $A B ⊥ C D$ 于点D， $∠ 1 = 50 °$ ，则 $∠ 2$ 的度数是（）

A、 $40 °$ B、 $45 °$ C、 $50 °$ D、 $60 °$

查看试题解析
4. 小强在证明“角的内部到角的两边的距离相等的点在角的平分线上”给出如下过程：
关于这个证明，下面说法正确的是(　　)

A、小强用到了从特殊到一般的方法证明该定理 B、只要测量一百个到角的两边的距离相等的点都在角的平分线上，就能证明该定理 C、不能只用这个角，还需要用其它角度进行测量验证，该定理的证明才完整 D、小强的方法可以用作猜想，但不属于严谨的推理证明

查看试题解析
5. 热爱帆船运动的聪聪同学用一副三角板拼成一幅“帆船图”.如图，已知∠D=∠BCA=90°，∠E=45°，若 $A C ‖ E F ， C A = C F$ ，连接AF ，则∠CAF的度数为( )

A、45° B、60° C、67.5° D、135°

查看试题解析
6. 如图， $△ A O B ≌ △ A D C ， ∠ O = ∠ D = 90 °$ ，记 $∠ O A D = α$ ， $∠ A B O = β$ ，当 $B C ∥ O A$ 时， $α$ 与 $β$ 之间的数量关系为（）

A、 $α = β$ B、 $α = 2 β$ C、 $α + β = 90 °$ D、 $α + 2 β = 180 °$

查看试题解析
7. 将一副三角板按如图方式放置，则下列结论：①∠1＝∠3；②如果∠2＝30°，则有AC∥DE；③如果∠2＝30°，则有BC∥AD；④如果∠2＝30°，必有∠4＝∠C.其中正确的有( )

A、①②③ B、①②④ C、③④ D、①②③④

查看试题解析

二、填空题（每题3分，共18分）

8. 光线在不同介质中的传播速度是不同的，因此当光线从水中射向空气时，要发生折射. 由于折射率相同，所以在水中平行的光线，在空气中也是平行的. 如图，a，b为两条平行的光线， $∠ 1 = 4 5^{°}$ ，则 $∠ 2$ 的度数为.

查看试题解析
9. 如图，∠1=140°，∠2=40°，∠3=108°，则∠4=时，AB∥EF.

查看试题解析
10. 如图，直线m $∥$ n，以直线m上的点A为圆心，适当长为半径画弧，分别交直线m，n于点B、C，连接AC、BC，若∠1＝30°，则∠2＝．

查看试题解析
11. 如图是一把椅子的侧面图，椅面 DE 与地面 AB 平行，∠DEC=60°，∠DCE=70°，则∠DBA的度数为.

查看试题解析
12. 如图，AB∥CD，∠BOC＝100°，BE，CF分别平分∠ABO，∠OCD，则∠2﹣∠1＝．

查看试题解析
13. 如图1是一个消防云梯，其示意图如图2所示，此消防云梯由救援台AB，延展臂BC（B在C的左侧），伸展主臂CD，支撑臂EF构成，在操作过程中，救援台AB，车身GH及地面MN三者始终保持平行，当 $∠ E F H = 5 5^{°}$ ， $B C / / E F$ 时， $∠ A B C =$ 度；如图3为了参与另外一项高空救援工作，需要进行调整，使得延展臂BC与支撑臂EF所在直线互相垂直，且 $∠ E F H = 7 8^{°}$ ，则这时 $∠ A B C =$ 度.

查看试题解析

三、解答题（共8题，共72分）

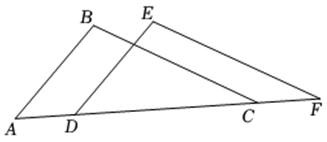14. 如图，点 $A$ ， $D$ ， $C$ ， $F$ 在同一条直线上， $AB = DE$ ， $BC = EF .$ 有下列三个条件： $① AC = DF$ ， $② ∠ ABC = ∠ DEF$ ， $③ ∠ ACB = ∠ DFE$ ．

(1)、请在上述三个条件中选取一个条件，使得 $△ ABC$ ≌ $△ DEF$ ．
你选取的条件为 ( 填写序号 ) ( 只需选一个条件，多选不得分 )，你判定 $△ ABC$ ≌ $△ DEF$ 的依据是 (填“ $SSS$ ”或“ $SAS$ ”或“ $ASA$ ”或“ $AAS$ ”)；

(2)、利用 $(1)$ 的结论 $△ ABC$ ≌ $△ DEF .$ 求证： $AB / / DE$ ．

查看试题解析
15. 如图，点A在MN上，点B在PQ上，连接AB，过点A作AC⊥AB交PQ于点C，过点B作BD平分∠ABC交AC于点D，且∠NAC＋∠ABC＝90°.

(1)、求证：MN∥PQ；

(2)、若∠ABC＝∠NAC＋10°，求∠ADB的度数.

查看试题解析
16. 如图， $∠ 1 = 5 2^{°}$ ， $∠ 2 = 12 8^{°}$ ， $∠ C = ∠ D$ .

(1)、求证： $B D ∥ C E$ .

(2)、探索 $∠ A$ 与 $∠ F$ 的数量关系，并说明理由.

查看试题解析
17. 已知 $M N ∥ P Q$ ，点 A，D 在直线 PQ 上，点 E，B 在直线 MN 上， $∠ E D B = 9 0^{°}$ ， BA 平分 $∠ E B D$ ， F 是直线 MN 上方一点，且 $∠ B E F = ∠ B A D$ .

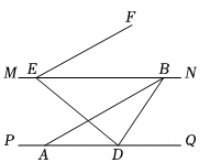(1)、 EF 与 AB 平行吗？请说明理由.

(2)、若 $∠ A D E = 3 6^{°}$ ，求 $∠ F E B$ 的度数.

查看试题解析
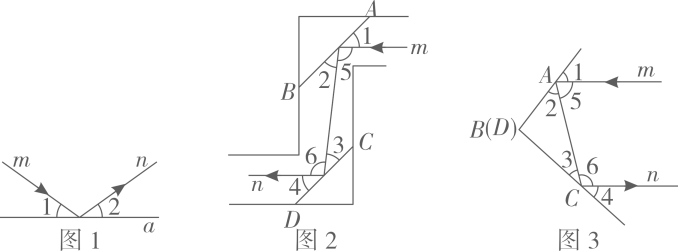18. 实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等．如图1，一束光线 $m$ 射到平面镜 $a$ 上，被 $a$ 反射后的光线为 $n$ ，则入射光线 $m$ 、反射光线 $n$ 与平面镜 $a$ 所夹的锐角 $∠ 1 = ∠ 2$ ．

(1)、利用这个规律人们制作了潜望镜，图2是潜望镜的工作原理示意图，AB、CD是平行放置的两面平面镜．已知光线经过平面镜反射时，有 $∠ 1 = ∠ 2, ∠ 3 = ∠ 4$ ，请判断入射光线 $m$ 和反射光钱 $π$ 是否平行，并说明理由．

(2)、显然，改变两面平面镜AB、CD之间的位置关系、经过两次反射后，入射光线 $m$ 与反射光线 $n$ 之间的位置关系会随之改变，如图3，一束光线 $m$ 射到平面镜AB上，被AB反射到平面镜CD上，又被CD反射．若被CD反射出的光线 $n$ 和光线 $m$ 平行，且 $∠ 1 = 4 7^{°}$ ，则 $∠ 6 =$ °， $∠ A B C =$ °．

(3)、试猜想：在图3中，当两平面镜AB，CD的夹角 $∠ A B C$ 的度数是多少时，可以使任何入射光线 $m$ 经过平面镜AB、CD的两次反射后，与反射光线 $n$ 平行？请说明理由．

查看试题解析
19. 在一次综合与实践课上，李老师让同学们以“两条平行线 $A B$ 、 $C D$ 和一块含 $60 °$ 角的直角三角尺 $E F G (∠ E F G = 90 °, ∠ E G F = 60 °)$ 的不同方式摆放”为主题开展数学探究活动．
【初步体验】
（1）如图①，三角尺的 $60 °$ 角的顶点 $G$ 在 $C D$ 上． $∠ 1 = 80 °$ ，则 $∠ 2$ 的度数为_____ $°$ ．
【基础巩固】
（2）如图②，彬彬把三角尺的两个锐角的顶点 $E$ ， $G$ 分别放在 $A B$ 和 $C D$ 上，请你探索 $∠ A E F$ 与 $∠ F G C$ 之间的数量关系，并说明理由．
【强化应用】
（3）如图③，强强把三角尺的直角顶点 $F$ 放在 $C D$ 上， $30 °$ 角的顶点 $E$ 在 $A B$ 上．若 $∠ A E G = α$ ， $∠ D F G = β$ ，请写出 $∠ A E G$ 与 $∠ D F G$ 的数量关系（用含 $α$ ， $β$ 的式子表示），并说明理由．

查看试题解析

北师大版数八年级上册单元分层检测卷-第七章 《命题与证明》B卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共8题，共72分）

北师大版数八年级上册单元分层检测卷-第七章《命题与证明》B卷