北师大版数八年级上册单元分层检测卷第七章 《命题与证明》A卷
试卷更新日期:2025-12-07 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 下列语句是命题的是( )A、你喜欢数学吗? B、小明是男生 C、城阳世纪公园 D、加强体育锻炼2. 下列命题中是假命题的是( )A、两点之间,线段最短 B、同旁内角互补 C、等角的补角相等 D、垂线段最短3. 如图两平行线a、b被直线l所截,且∠1=60°,则∠2的度数为
 A、30° B、45° C、60° D、120°4. 图1 是视觉错觉艺术风格的作品,这种设计利用背景线条、图案的干扰,制造出视觉认知偏差的冲突,具有很强的趣味性与迷惑性.如图2,现将其中的一组背景线条与直线a,b抽象出来,下列说法能判断出的是( )
A、30° B、45° C、60° D、120°4. 图1 是视觉错觉艺术风格的作品,这种设计利用背景线条、图案的干扰,制造出视觉认知偏差的冲突,具有很强的趣味性与迷惑性.如图2,现将其中的一组背景线条与直线a,b抽象出来,下列说法能判断出的是( ) A、 B、 C、 D、5. 下列图形中, 由∠1=∠2, 能得到AB∥CD的是( )A、
A、 B、 C、 D、5. 下列图形中, 由∠1=∠2, 能得到AB∥CD的是( )A、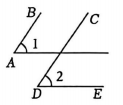 B、
B、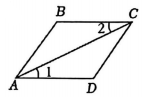 C、
C、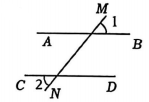 D、
D、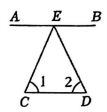 6. 如图,一条输电线路需跨越一个池塘,池塘两侧A,B处各立有一根电线杆,但利用现有皮尺无法直接最出A,B间的距离。为此,小明和小华两位同学提供了如下测量方案:
6. 如图,一条输电线路需跨越一个池塘,池塘两侧A,B处各立有一根电线杆,但利用现有皮尺无法直接最出A,B间的距离。为此,小明和小华两位同学提供了如下测量方案:方案1
①如图1,选定点O;
②连接AO,并延长到点C,使OC=OA,连接BO,并延长到点D,使OD=OB:
③连接DC,测量DC的长度即可。
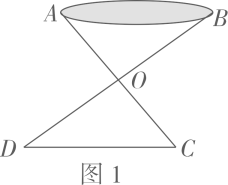
方案2
①如图2,选定点O:
②连接AO,BO,并分别延长到点F,E,使OF=OB,OE=OA:
③连接EF,测量EF的长度即可。
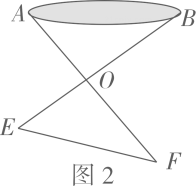
对于方案1和方案2,下列说法正确的是( )
A、1、2都不可行 B、1不可行、2可行 C、1可行、2不可行 D、1、2都可行7. 如图,A,D,E三点共线,下列条件中能判断直线的是( ) A、 B、 C、 D、8. 下列语句中,是命题的是( )
A、 B、 C、 D、8. 下列语句中,是命题的是( )①若∠1=60°,∠2=60°,则∠1=∠2;②同位角相等吗?③画线段AB=CD;④如果a>b,b>c,那么a>c;⑤直角都相等.
A、①④⑤ B、①②④ C、①②⑤ D、②③④⑤9. 如图,过直线外一点画已知直线的平行线的方法叫“推平行线”法(图中三角形是三角板),其依据是( ) A、同旁内角互补,两直线平行 B、两直线平行,同旁内角互补 C、同位角相等,两直线平行 D、两直线平行,同位角相等10. 如图,直线 , 一直角三角板ABC(∠ACB=90° )放在平行线上,两直角边分别l1与l2、交于点D、E,现测得∠1=75° , 则∠2的度数为( )
A、同旁内角互补,两直线平行 B、两直线平行,同旁内角互补 C、同位角相等,两直线平行 D、两直线平行,同位角相等10. 如图,直线 , 一直角三角板ABC(∠ACB=90° )放在平行线上,两直角边分别l1与l2、交于点D、E,现测得∠1=75° , 则∠2的度数为( ) A、15° B、25° C、30° D、35°
A、15° B、25° C、30° D、35°二、填空题(每题3分,共18分)
-
11. 如图, , , 图中两个三角形是否全等?(填“是”或“否”),如果全等,请写出与边相等的对应边 .
 12. 如图,将一块三角尺的直角顶点放在直尺的一边上,当时,的度数为 .
12. 如图,将一块三角尺的直角顶点放在直尺的一边上,当时,的度数为 . 13. 命题“若 , 则”是命题.(填“真”或“假”)14. 如图是小颖同学做仰卧起坐运动某一瞬间的动作及其示意图, , , 则的度数为 .
13. 命题“若 , 则”是命题.(填“真”或“假”)14. 如图是小颖同学做仰卧起坐运动某一瞬间的动作及其示意图, , , 则的度数为 . 15. 把命题“对顶角相等”改写成“如果…那么…”的形式:16.
15. 把命题“对顶角相等”改写成“如果…那么…”的形式:16.如图,直线a与直线b、c分别相交于点A、B,将直线b绕点A转动,当∠1=∠时,c∥b

三、解答题(共8题,共72分)
-
17. 将下列证明过程补充完整:
已知:如图,点分别在上,分别交于点 , .
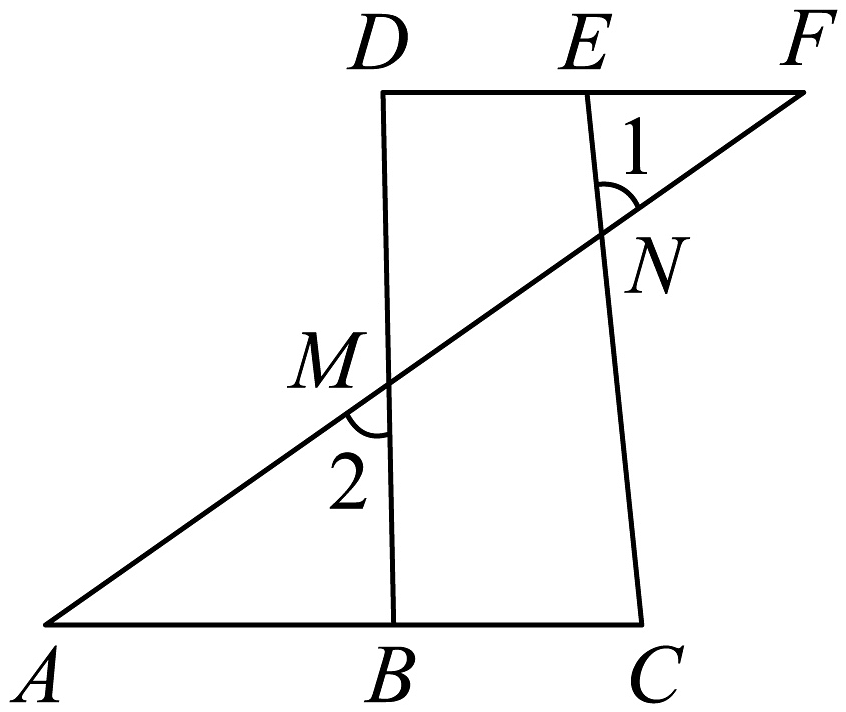
求证: .
证明:因为(已知)
又因为(____________),
所以___________(等量代换).
所以( )
所以(____________).
又因为(已知),
所以(____________).
所以__________( ).
所以( ).
18. 如图,在中,为上一点,为中点,连接并延长至点 , 使得 . (1)、求证:;(2)、连接 , 若平分平分 , 且 , 求的度数.19. 如图1,点为边上一点,
(1)、求证:;(2)、连接 , 若平分平分 , 且 , 求的度数.19. 如图1,点为边上一点, (1)、利用直尺和圆规:过点作直线 , 使 . (用黑色水笔描出作图痕迹,不要求写作法)(2)、如图2,在(1)的前提下,为上一点,过作 , 求证: .20. 如图,已知点在直线上,点在线段上,与交于点 .
(1)、利用直尺和圆规:过点作直线 , 使 . (用黑色水笔描出作图痕迹,不要求写作法)(2)、如图2,在(1)的前提下,为上一点,过作 , 求证: .20. 如图,已知点在直线上,点在线段上,与交于点 . (1)、求证:;(2)、若 , 求的度数.21. 如图,在中,D为上一点,E为中点,连接DE并延长至点F,使得 , 连接 .
(1)、求证:;(2)、若 , 求的度数.21. 如图,在中,D为上一点,E为中点,连接DE并延长至点F,使得 , 连接 . (1)、求证:;(2)、若 , 连接平分平分 , 求的度数.22. 如图, .
(1)、求证:;(2)、若 , 连接平分平分 , 求的度数.22. 如图, . (1)、求证: .
(1)、求证: .小颖同学是这样做的,请你将证明过程补充完整.
证明:如图1,过点作 ,
(2)、如图2,若 , 分别平分和 , 则与之间的等量关系为_________.