鲁教版（五四制）数学九年级上学期期末仿真模拟试卷（二）[范围：九上全册]

试卷更新日期：2025-12-05 类型：期末考试

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 二次函数y = $- \frac{1}{2}$ （x-3）²+4的图象的开口方向、对称轴、顶点坐标分别是（）

A、向上，直线x=3，（3，4） B、向上，直线x=-3，（3，4） C、向上，直线x=3，（3，-4） D、向下，直线x=3，（3，4）

查看试题解析
2. 在 Rt△ABC中，∠C= 90°，若 △ABC的三边都放大2倍，则 sinA的值（）

A、缩小 2 倍 B、放大 2 倍 C、不变 D、无法确定

查看试题解析
3. 某几何体的三视图如图所示，则该几何体为（）

A、 B、 C、 D、

查看试题解析
4. 在同一坐标系中画出 $y_{1} = 2 x^{2}, y_{2} = - 2 x^{2}, y_{3} = \frac{1}{2} x^{2}$ 的图象，正确的是（）

A、 B、 C、 D、

查看试题解析
5. 如图，在直角坐标系中，点 $A (0, a^{2} + a)$ 和点 $B (0, - a - 2)$ 在 $y$ 轴上，点 $M$ 在 $x$ 轴负半轴上， $S_{△ A B M} = 2$ ，当线段 $O M$ 最长时，点 $M$ 的坐标为（）

A、(-2， 0) B、(-3， 0) C、(-4， 0) D、(-5， 0)

查看试题解析
6. 某商品现在的售价为每件60元，每星期可卖出300件．市场调查反映：如调整价格，每涨价1元，每星期要少卖出10件；每降价1元，每星期可多卖出20件．已知商品的进价为每件40元，据以上信息得出下列结论，其中错误的是（　　）

A、定价70元时，利润为6000元 B、定价 $56.5$ 元时，利润为6105元 C、降价3元，能使所获利润最大 D、涨价5元，能使所获利润最大

查看试题解析
7. 如图，函数 $y = - \frac{3}{4} (x - 4) (x + 1)$ 的图象与x轴交于A ， B两点（A在B的左侧），与y轴交于点C ，点P是BC上方抛物线上一点，连结AP交BC于点D ，连结AC ， CP ，记△ACD的面积为S₁ ， △PCD的面积为S₂ ，则 $\frac{S_{2}}{S_{1}}$ 的最大值为（　　）

A、1 B、 $\frac{4}{5}$ C、 $\frac{3}{4}$ D、 $\frac{3}{5}$

查看试题解析
8. 我们定义一种新函数：形如 $y = | a x^{2} + b x + c | (a \neq 0, b^{2} - 4 a c > 0)$ 的函数叫做“鹊桥”函数．某数学兴趣小组画出了“鹊桥”函数 $G : y = | x^{2} - x - 6 |$ 的图象（如图所示），并写出了下列结论：
①图象与坐标轴的交点为 $A (- 2, 0)$ ， $B (3, 0)$ ， $C (0, 6)$ ；
②当 $x = \frac{1}{2}$ 时，函数取得最大值；
③当 $- 2 \leq x \leq \frac{1}{2}$ 或 $x ≥ 3$ 时，函数值 $y$ 随 $x$ 值的增大而增大；
④若 $(x_{0}, y_{0})$ 在函数图象上，则 $(1 - x_{0}, y_{0})$ 也在函数图象上；
⑤当直线 $y = - x + m$ 与函数 $G$ 的图象有 $2$ 个交点时，则 $m$ 的取值范围是 $- 2 < m < 3$ ．其中正确的结论有（）

A、①②③ B、②③④ C、①④⑤ D、①③④

查看试题解析

二、填空题：本大题共5小题，每小题3分，共15分。

9. 已知二次函数. $y = 2 x^{2} - x + k - 2$ 的图象与x轴有交点，则k的取值范围是.

查看试题解析
10. 如图，在矩形 $A B C D$ 中， $A B = 3$ ， $A D = 5$ ，点 $E$ 在 $D C$ 上，将矩形 $A B C D$ 沿 $A E$ 折叠，点 $D$ 恰好落在 $B C$ 边上的点 $F$ 处，那么 $\sin ∠ E F C$ 的值为．

查看试题解析
11. 某三棱柱的三种视图如图所示，它的主视图是三角形，左视图和俯视图都是矩形，且俯视图的面积是左视图面积的 $2$ 倍，左视图中矩形 $A B C D$ 的边长 $A B = 3$ ，则主视图的面积为．

查看试题解析
12. 如图，在四边形ABCD 中，AB=BC=6 cm，CD=AD=6 $\sqrt{3}$ cm，∠B=120°.点E从点B出发，沿BC边向点C以1cm/s的速度移动；点F从点C出发，沿CD边向点D以1cm/s的速度移动.E、F同时出发，当其中一点到达终点时，运动停止，连结AE，EF，AF，设运动的时间为t（S），若使△AEF的面积为最小，则t的值是.

查看试题解析
13. 如图， $A$ ， $B$ 是抛物线 $y = x^{2}$ 上两点，点 $P$ 为 $A B$ 的中点，过点 $P$ 作 $x$ 轴的垂线，交抛物线于点 $Q$ ， $P Q = 3$ ．设 $A$ ， $B$ 两点的横坐标分别为 $x_{1}$ ， $x_{2} (x_{2} > x_{1})$ ．则 $x_{2} - x_{1}$ 的值为．

查看试题解析

三、解答题：本大题共8小题，共75分。

14. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， D为边 $B C$ 上的一点， $B C = 6$ ， $\tan B = \frac{2}{3}$ ．

(1)、求 $A C$ 的长．

(2)、若 $A C - C D = 2$ ，求 $\sin ∠ C A D$ 的值．

查看试题解析
15. 已知y=（m+1） $x^{m^{2} + m}$ 是二次函数，且当x＞0时，y随x的增大而减小．

(1)、求m的值；

(2)、当自变量的值为多少时，函数有最值？最值是多少？

查看试题解析
16. 如图，已知反比例函数 $y = \frac{k}{x}$ 的图象与直线 $y = - 3 x - 3$ 相交于 $A (- 2, m)$ ， B两点．

(1)、求k的值．

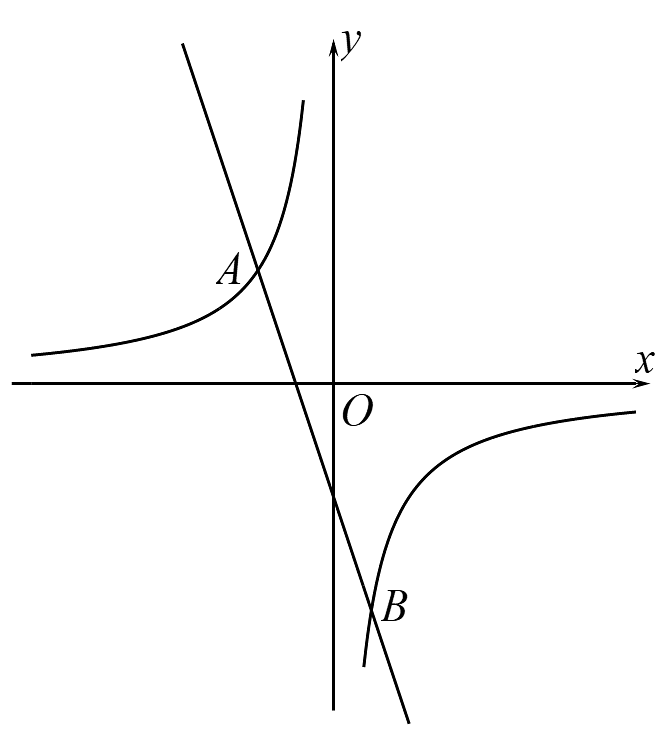(2)、当 $\frac{k}{x} > - 3 x - 3$ 时，请直接写出x的取值范围．

查看试题解析
17. 由几个小立方体叠成的几何体的主视图和左视图如图所示，求组成几何体的小立方体个数的最大值与最小值，并画出相应的俯视图.

查看试题解析
18. 已知反比例函数 $y = \frac{k}{x}$ 的图象经过点 $(- 2 ， 5)$ ．

(1)、求y与x之间的函数表达式；

(2)、这个函数的图象在哪个象限？在每个象限内，y随x的增大怎样变化？

(3)、判断点 $P (- \frac{1}{10}, - 1)$ 是否在这个函数的图象上，说明理由．

查看试题解析
19. 如图，是一个抛物线形拱桥，以拱顶O为坐标原点建立平面直角坐标系，当拱顶O离水面BC的高OA=2m时，水面宽BC=4m.

(1)、求该抛物线表示的二次函数解析式；

(2)、当水面BC下降1m到达EF时，求水面宽度增加多少m？

查看试题解析
20. 定义：若一个点的纵坐标是横坐标的3倍，则称这个点为“三倍点”，如： $A (1, 3)$ ， $B (- 2, - 6)$ ， $C (0, 0)$ 等都是“三倍点”．已知二次函数 $y = - x^{2} - x + c$ （ $c$ 为常数）．

(1)、若该函数经过点 $(1, - 6)$ ，求该函数图象上的“三倍点”坐标；

(2)、在（1）的条件下，当 $t \leq x \leq t + 2$ 时，求该函数的最小值（用含 $t$ 的代数式表示）；

(3)、在 $- 4 < x < 1$ 的范围内，若二次函数 $y = - x^{2} - x + c$ 的图象上至少存在一个“三倍点”，求 $c$ 的取值范围．

查看试题解析