鲁教版（五四制）数学八年级上学期期末仿真模拟试卷（二）

试卷更新日期：2025-12-05 类型：期末考试

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列条件中能判定四边形 $A B C D$ 是平行四边形的是（）

A、 $∠ A = ∠ B$ ， $∠ C = ∠ D$ B、 $A B = A D$ ， $C B = C D$ C、 $A B = C D$ ， $A D = B C$ D、 $A B // C D$ ， $A D = B C$

查看试题解析
3. 某中学篮球队 $13$ 名队员的年龄情况如下：
年龄 $（$ 单位：岁 $)$
$14$
$15$
$16$
$17$
$18$
人数
$2$
$4$
$3$
$2$
$2$
则这个队队员年龄的众数和中位数分别是（ )

A、 $15$ ， $15.5$ B、 $15$ ， $15$ C、 $15$ ， $16$ D、 $16$ ， $15$

查看试题解析
4. 下列由左到右的变形，属于因式分解的是（）

A、 $(x + 2) (x - 2) = x^{2} - 4$ B、 $x^{2} - 4 = (x + 2) (x - 2)$ C、 $x^{2} - 4 + 3 x = (x + 2) (x - 2) + 3 x$ D、 $x^{2} + 4 x - 2 = x (x + 4) - 2$

查看试题解析
5. 在日常生活中，经常会用到密码，有一种利用“因式分解”法生成的密码，方便记忆.如将 $x^{2} - 9$ 因式分解的结果为（x-3）（x+3），取个人年龄作为x的值，当x=13时，x-3=10，x+3=16，由此可以得到数字密码1016.小旭按这种方式将 $x^{3} - x$ 因式分解后，取自己的年龄14设置了一个密码，他设置的密码可能是（）

A、141414 B、141315 C、131413 D、151415

查看试题解析
6. 如图，在□ABCD中，AB=2，∠D=45°，∠ACD=90°，M是AD的中点，E是AB延长线上的动点，作∠EMF=90°交AC的延长线于点F.记BE=x，CF=y，当x，y的值发生变化时，下列代数式的值不变的是（）

A、 $x + y$ B、 $x - y$ C、xy D、 $\frac{x}{y}$

查看试题解析
7. 如图，平行四边形 $A B C D$ 的对角线 $A C$ ， $B D$ 相交于点 $O$ ， $∠ A B C = 60^{\circ}$ ， $A B = 2 B C$ ， $E$ 是 $A B$ 的中点，连接 $C E$ ， $O E$ .下列结论： $① ∠ A C D = 30^{\circ}$ ； $② C E$ 平分 $∠ D C B$ ； $③ C D = 4 O E$ ； $④ S_{△ C O E} = \frac{1}{6} S_{四边形 A B C D}$ .其中结论正确的序号是（）

A、①② B、②③④ C、①②③ D、①③④

查看试题解析
8. 如图，在长方形 $A B C D$ 中， $A C$ 是对角线，将长方形 $A B C D$ 绕点B顺时针旋转 $90 °$ 到长方形 $G B E F$ 的位置，H是 $E G$ 的中点，若 $A B = 3$ ， $B C = 4$ ，则线段 $C H$ 的长为（）

A、 $\sqrt{5}$ B、 $\frac{\sqrt{41}}{2}$ C、 $\sqrt{10}$ D、 $\frac{\sqrt{21}}{2}$

查看试题解析
9. 如图，在 $▱ A B C D$ 中， $B E$ 垂直平分 $C D$ 于点E， $∠ B A D = 45 °$ ， $A D = 2$ ，则 $▱ A B C D$ 的对角线 $A C$ 的长为（）

A、5 B、10 C、 $\frac{2}{3}$ D、 $2 \sqrt{5}$

查看试题解析
10. 如图，点 $P$ 为定角 $∠ A O B$ 的平分线上的一个定点，且 $∠ M P N$ 与 $∠ A O B$ 互补，若 $∠ M P N$ 在绕点 $P$ 旋转的过程中，其两边分别与 $O A ， O B$ 交于点 $M ， N$ ，则一下结论：① $P M = P N$ 恒成立；② $O M + O N$ 的值不变；③四边形 $P M O N$ 的面积不变；④ $M N$ 的长不变；其中正确的个数为（　　）个

A、1 B、2 C、3 D、4

查看试题解析

二、填空题：本大题共5小题，每小题3分，共15分.

11. 若样本数据x₁＋1，x₂＋1，…，x_n＋1的平均数是5，方差是2，则样本数据2x₁＋2，2x₂＋2，…，2x_n＋2的平均数、方差分别是。

查看试题解析
12. 若关于x的分式方程 $\frac{m}{x - 1} + \frac{3}{1 - x} = 1$ 无解，则m的值是．

查看试题解析
13. 如图，分别以 Rt△ABC 的直角边AC 及斜边AB 为边向外作等边三角形ACD、等边三角形 ABE，EF⊥AB 于点 F，连接 DF，当 $\frac{A C}{A B} =$ 时，四边形ADFE 是平行四边形.

查看试题解析
14. 如图，在□ABCD中，连接AC，将△ACD绕点A顺时针旋转一定角度，得到△AEF，点C，D分别旋转到了点E，F.已知点E在边BC上，AD=5，EF=2 $\sqrt{13}$ ， BE=3，则AE的长为.

查看试题解析
15. 如图，在平行四边形ABCD中，∠C=120°，AD=4，AB=2，点H、G分别是边CD、BC上的动点．连接AH、HG ，点E为AH的中点，点F为GH的中点，连接EF则EF的最大值与最小值的差为．

查看试题解析

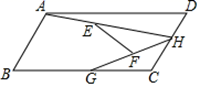
三、解答题：本大题共8小题，共75分.

16. 解方程： $\frac{6}{x - 1} - \frac{x + 5}{x^{2} - x} = 0$ .

查看试题解析
17. 如图， $△ A B C$ 三个顶点的坐标分别是A $(1, 1)$ ， B $(4, 2)$ ， C $(3, 4)$ ．

(1)、请画出 $△ A B C$ 向左平移5个单位长度，再向上平移1个单位长度后得到的 $△ A_{1} B_{1} C_{1}$ ；

(2)、请画出 $△ A B C$ 关于原点对称的 $△ A_{2} B_{2} C_{2}$ ，并写出 $B_{2}$ 的坐标；

(3)、求出 $△ A B C$ 的面积．

查看试题解析
18. 某工厂生产部门为了解本部门工人的生产能力情况，进行了抽样调查．该部门随机抽取了30名工人某天每人加工零件的个数，数据如下：
20
21
19
16
27
18
31
29
21
22
25
20
19
22
35
33
19
17
18
29
18
35
22
15
18
18
31
31
19
22
整理上面数据，得到条形统计图：
样本数据的平均数、众数、中位数如下表所示：
统计量
平均数
众数
中位数
数值
23
m
21
根据以上信息，解答下列问题：
（1）上表中众数m的值为　　；
（2）为调动工人的积极性，该部门根据工人每天加工零件的个数制定了奖励标准，凡达到或超过这个标准的工人将获得奖励．如果想让一半左右的工人能获奖，应根据　　来确定奖励标准比较合适．（填“平均数”、“众数”或“中位数”）
（3）该部门规定：每天加工零件的个数达到或超过25个的工人为生产能手．若该部门有300名工人，试估计该部门生产能手的人数．

查看试题解析
19. 一个多边形的内角和比它的外角和的2倍多 $180 °$ ，求这个多边形的边数．

查看试题解析
20. 如图，已知AB＝DC ， AB∥CD ， E、F是AC上两点，且AE＝CF ．

(1)、求证：△ABF≌△CDE；

(2)、若∠BCE＝30°，∠CBF＝20°，求∠CED的度数．

查看试题解析
21. 如图，在▱ABCD中，∠ABC的平分线与CD的延长线相交于点E，与AD 相交于点F，且点 F恰好为边AD 的中点，连接AE.

(1)、求证：四边形ABDE 是平行四边形；

(2)、若AG⊥BE于点G，BC=6，AG=2，求 EF的长.

查看试题解析
22. 如图， $▱ A B C D$ 的对角线 $A C$ ， $B D$ 相交于点O， $∠ A D C$ 的平分线与边 $A B$ 相交于点E，P是 $D E$ 的中点，若 $A D = 5$ ， $C D = 9$ ，求 $P O$ 的长．

查看试题解析
23. 平行四边形 $A B C D$ 中， $A B ⊥ A C$ ，点E在边 $A D$ 上，连接 $B E$ .

(1)、如图1， $A C$ 交 $B E$ 于点G，若 $B E$ 平分 $∠ A B C$ ，且 $∠ D A C = 30 °$ ， $C G = 2$ ，请求出四边形 $E G C D$ 的面积；

(2)、如图2，点F在对角线 $A C$ 上，且 $A F = A B$ ，连接 $B F$ ，过点F作 $F H ⊥ B E$ 于H，连接 $A H$ ，求证： $H F + \sqrt{2} A H = B H$ .

(3)、如图3，线段 $P Q$ 在线段 $B E$ 上运动，点R在边 $B C$ 上，连接 $C Q ， P R$ .若 $B E$ 平分 $∠ A B C$ ， $∠ D A C = 30 °$ ， $A B = \sqrt{3}$ ， $P Q = \frac{3}{2}$ ， $B C = 4 B R$ .请直接写出线段 $C Q + P Q + P R$ 的和的最小值以及此时 $△ C Q E$ 的面积.

查看试题解析

年龄 $（$ 单位：岁 $)$	$14$	$15$	$16$	$17$	$18$
人数	$2$	$4$	$3$	$2$	$2$

20	21	19	16	27	18	31	29	21	22
25	20	19	22	35	33	19	17	18	29
18	35	22	15	18	18	31	31	19	22

统计量	平均数	众数	中位数
数值	23	m	21

20	21	19	16	27	18	31	29	21	22
25	20	19	22	35	33	19	17	18	29
18	35	22	15	18	18	31	31	19	22

20	21	19	16	27	18	31	29	21	22
25	20	19	22	35	33	19	17	18	29
18	35	22	15	18	18	31	31	19	22