沪科版数学八年级上册期末质量检测卷(二)
试卷更新日期:2025-12-04 类型:期末考试
一、选择题(每题4分,共40分)
-
1. 在平面直角坐标系中,点一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 汉字是中华文明的标志,从公元前16世纪段商后期的被认为是汉字的第一种形式的甲骨文到
今天,产生了金文、小篆、隶书、楷书,草书、行书等多件字体,每种字体都有着各自鲜明的艺术特征. 下面的小篆体字是轴对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 3. 如图,为了估计池塘两岸A,B的距离,在池塘的一侧取点P,测得PA=14米,PB=9米,那么A,B间的距离不可能是 ( )
3. 如图,为了估计池塘两岸A,B的距离,在池塘的一侧取点P,测得PA=14米,PB=9米,那么A,B间的距离不可能是 ( ) A、6米 B、8.7米 C、27米 D、18米4. 若点在过原点的一条直线上,则这条直线所对应的函数解析式为( )A、 B、 C、 D、5. 如果一次函数与的交点坐标为 , 那么是下列哪个方程组的解( )A、 B、 C、 D、6. 如图,在中,和的平分线相交于点P,连接PA,PB,PC,若 , , 的面积分别为 , , , 则有( )
A、6米 B、8.7米 C、27米 D、18米4. 若点在过原点的一条直线上,则这条直线所对应的函数解析式为( )A、 B、 C、 D、5. 如果一次函数与的交点坐标为 , 那么是下列哪个方程组的解( )A、 B、 C、 D、6. 如图,在中,和的平分线相交于点P,连接PA,PB,PC,若 , , 的面积分别为 , , , 则有( ) A、 B、 C、 D、7. 如图表示光线从空气进入水中时的光路图,若按如图所示的方式建立平面直角坐标系,并设入水前与入水后光线所在直线的函数表达式分别为 则关于 k1与k2的关系,下列说法正确的是( )
A、 B、 C、 D、7. 如图表示光线从空气进入水中时的光路图,若按如图所示的方式建立平面直角坐标系,并设入水前与入水后光线所在直线的函数表达式分别为 则关于 k1与k2的关系,下列说法正确的是( ) A、k1>0,k2<0 B、 C、 D、8. 如图是甲,乙两车在某时段速度随时间变化的图象,则下列说法错误的是( )
A、k1>0,k2<0 B、 C、 D、8. 如图是甲,乙两车在某时段速度随时间变化的图象,则下列说法错误的是( ) A、乙车前 6 秒行驶的路程为 48 米 B、在 0 到 6 秒内甲车的速度每秒增加 米 C、当两车速度相等时,乙车行驶了 19.6 米
A、乙车前 6 秒行驶的路程为 48 米 B、在 0 到 6 秒内甲车的速度每秒增加 米 C、当两车速度相等时,乙车行驶了 19.6 米
D、在第 3 秒到第 9 秒内甲车的速度都大于乙车的速度
9. 如图,中, , 、是边的中线,有;垂足为点交于点 . 且平分交于 . 交于 . 连接 . 则下列结论:①;②;③;④;
错误的有( )个.
 A、0 B、1 C、3 D、4
A、0 B、1 C、3 D、4二、填空题(每题5分,共30分)
-
10. 若函数有意义,则自变量取值范围为 .11. 对于a、b的取值,能够说明命题“若 , 则”是假命题的反例是 .12. 如图,已知 , 的延长线交于点F, , , 则 .
 13. 如图,直线的解析式为分别与 , 轴交于两点,点的坐标为 , 过点的直线交轴负半轴于点 , 且 , 在轴上方存在点 , 使以点为顶点的三角形与全等,则点的坐标为 .
13. 如图,直线的解析式为分别与 , 轴交于两点,点的坐标为 , 过点的直线交轴负半轴于点 , 且 , 在轴上方存在点 , 使以点为顶点的三角形与全等,则点的坐标为 . 14. 为等边三角形,点E在边上, , 在射线上取点D,使 , 连接并延长交射线于点F,则下列说法正确的是: .
14. 为等边三角形,点E在边上, , 在射线上取点D,使 , 连接并延长交射线于点F,则下列说法正确的是: .①当时,为等腰三角形;
②;
③在边上存在点E,使;
④ .
 15. 定义:对于给定的一次函数、为常数,且 , 把形如的函数称为一次函数的“新生函数”.已知一次函数 , 若点在这个一次函数的“新生函数”图象上,则的值是 ;若点在这个一次函数的“新生函数”图象上,则的值是 .
15. 定义:对于给定的一次函数、为常数,且 , 把形如的函数称为一次函数的“新生函数”.已知一次函数 , 若点在这个一次函数的“新生函数”图象上,则的值是 ;若点在这个一次函数的“新生函数”图象上,则的值是 .三、解答题(共8题,共80分)
-
16. 如图,在平面直角坐标系中,各顶点的坐标分别为 , , .
 (1)、作出与关于轴对称的图形;(2)、已知点 , 直线轴,求点的坐标.17. 如图:已知直线经过点 .
(1)、作出与关于轴对称的图形;(2)、已知点 , 直线轴,求点的坐标.17. 如图:已知直线经过点 .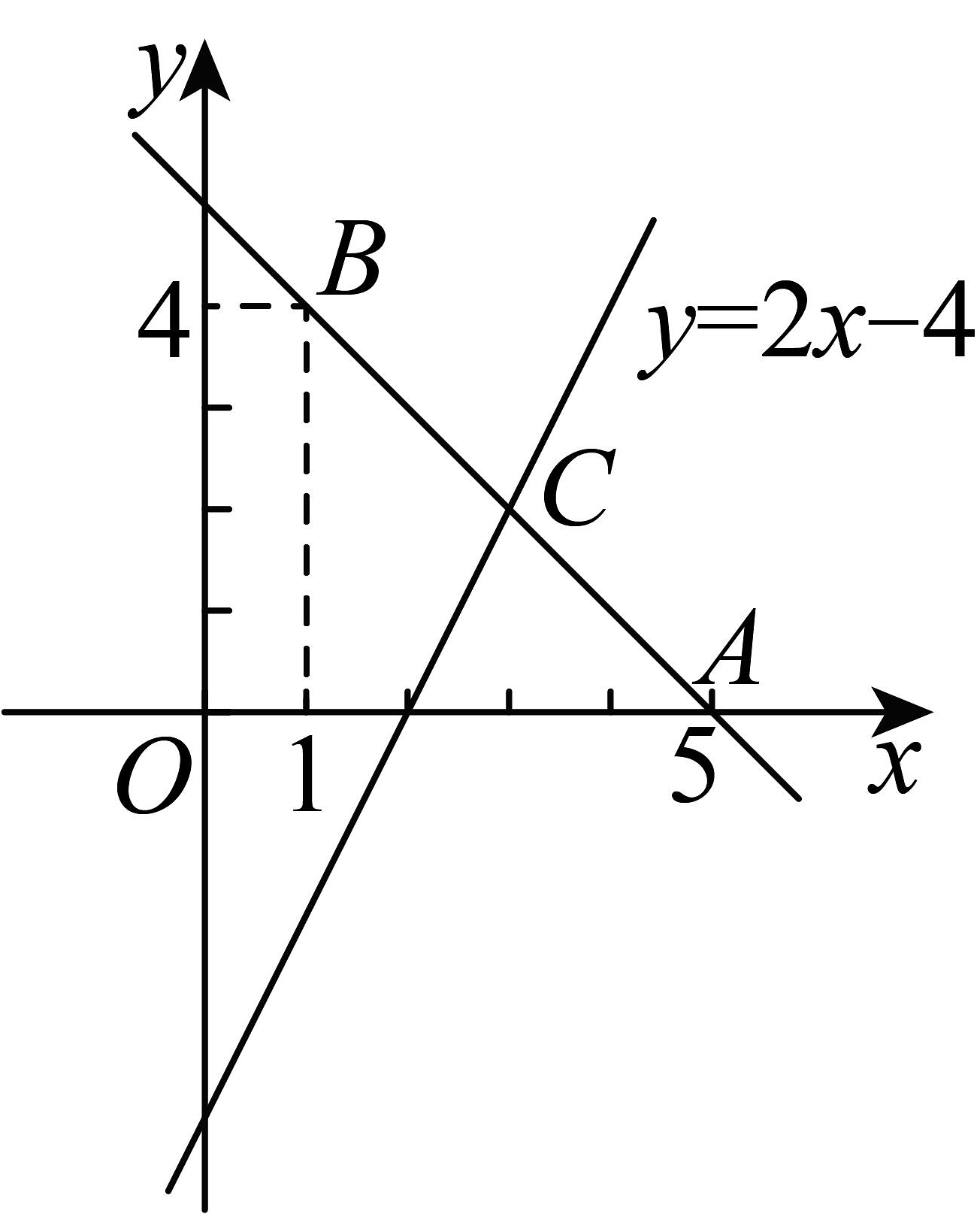 (1)、求直线的解析式;(2)、若直线与直线相交于点C,求点C的坐标;(3)、根据图象,直接写出关于x的不等式的解集.18. 如图,在中, , 垂直平分 , 的角平分线交于内一点P,连接 . 若 , 求的度数.
(1)、求直线的解析式;(2)、若直线与直线相交于点C,求点C的坐标;(3)、根据图象,直接写出关于x的不等式的解集.18. 如图,在中, , 垂直平分 , 的角平分线交于内一点P,连接 . 若 , 求的度数. 19. 第五代移动通信技术(简称5G)是最新一代蜂窝移动通信技术,是4G、3G和2G系统后的延伸.5G的性能目标是高数据速率、减少延迟、节省能源、降低成本、提高系统容量和大规模设备连接.县电信部门要修建一座5G信号发射塔,要求发射塔离村庄A、B的距离必须相等,且到两条高速公路MN、PQ的距离也必须相等.发射塔点G应修建在什么位置?在图上标出它的位置.(请保留作图痕迹,并标注出点G,否则扣分.)
19. 第五代移动通信技术(简称5G)是最新一代蜂窝移动通信技术,是4G、3G和2G系统后的延伸.5G的性能目标是高数据速率、减少延迟、节省能源、降低成本、提高系统容量和大规模设备连接.县电信部门要修建一座5G信号发射塔,要求发射塔离村庄A、B的距离必须相等,且到两条高速公路MN、PQ的距离也必须相等.发射塔点G应修建在什么位置?在图上标出它的位置.(请保留作图痕迹,并标注出点G,否则扣分.) 20. 已知甲、乙两个仓库分别有物资800 吨和1200 吨,现要把这些物资全部运往A,B 两地,A 地需要物资1300 吨,B地需要物资700吨,从甲、乙两仓库把物资运往A,B两地的运费单价如下表:
20. 已知甲、乙两个仓库分别有物资800 吨和1200 吨,现要把这些物资全部运往A,B 两地,A 地需要物资1300 吨,B地需要物资700吨,从甲、乙两仓库把物资运往A,B两地的运费单价如下表:A地(元/吨)
B地(元/吨)
甲仓库
12
15
乙仓库
10
18
(1)、设甲仓库运往A 地 x吨物资,直接写出总运费y(元)关于x(吨)的函数表达式(不需要写出自变量的取值范围);(2)、当甲仓库运往A 地多少吨物资时,总运费最少?总运费最少是多少?(3)、若甲仓库运往 A 地的运费下降了 a 元/吨后(2≤a≤6且a为常数),最少的总运费为23 100元,求a 的值.21. 已知,与都是等腰直角三角形, , , , 如图,连接、 . (1)、如图1,求证:;(2)、如图2,点D在内,B、D、E三点在同一直线上.
(1)、如图1,求证:;(2)、如图2,点D在内,B、D、E三点在同一直线上.①过点A作的高 , 证明:;
②如图3,若平分 , 交于点G , , 求的长.