冀教版数学八年级上册期末检测卷（一）

试卷更新日期：2025-12-04 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共36分）

1. 下列七个实数： $0$ ， $\sqrt{8}$ ， $\frac{22}{7}$ ， $\frac{π}{3}$ ， $\sqrt{16}$ ， $3.14159265$ ， $0.101001000100001 \dots$ ，其中无理数的个数是（）

A、 $2$ 个 B、 $3$ 个 C、 $4$ 个 D、 $5$ 个

查看试题解析
2. 围棋起源于中国，古代称之为“弈”，至今已有 $4000$ 多年的历史 $.$ 以下是在棋谱中截取的四个部分，由黑白棋子摆成的图案是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 关于全等图形的描述，下列说法正确的是（）

A、形状相同的图形 B、面积相等的图形 C、能够完全重合的图形 D、周长相等的图形

查看试题解析
4. 式子 $\frac{\sqrt{a + 3}}{a - 1}$ 有意义，则实数a的取值范围是（）

A、 $a \geq 3$ B、 $a \neq 1$ C、 $a \geq - 3$ 且 $a \neq 1$ D、 $a > - 3$ 且 $a \neq 1$

查看试题解析
5. 如图，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形．他的依据是（）

A、 $S A S$ B、 $A S A$ C、 $A A S$ D、 $S S S$

查看试题解析
6. 下列分式中，是最简分式的是（）

A、 $\frac{3 x y}{x^{2}}$ B、 $\frac{x - 1}{x^{2} - 1}$ C、 $\frac{x + y}{2 x}$ D、 $\frac{1 - x}{x - 1}$

查看试题解析
7. 将一副直角三角尺如图放置，若∠AOD=20°，则∠BOC的大小为（）

A、140° B、160° C、170° D、150°

查看试题解析
8. “等腰三角形的两个底角相等”的逆命题是（）

A、在同一个三角形中，等边对等角 B、两个角互余的三角形是等腰三角形 C、如果一个三角形有两个角相等，那么这个三角形是等腰三角形 D、如果一个三角形有三个角相等，那么这个三角形是等边三角形

查看试题解析
9. 暑假期间，嘉琪在家里看《西游记》，电视中“十万天兵对孙悟空兴师问罪”，嘉琪联想到这学期学过的数学知识．提出了如下问题：（1）10万用科学记数法怎么表示？（2）10万是准确数还是近似数？下列四个选项正确的是（）

A、 $10 \times 10^{4}$ ，准确数 B、 $10^{5}$ ，准确数 C、 $10^{5}$ ，近似数 D、 $1 \times 10^{5}$ ，近似数

查看试题解析
10. 如图，H是 $△ A B C$ 的高 $A D 、 B E$ 的交点，且 $A D = B E$ ，则下列结论中正确的有① $A E = B D$ ， ② $A H = B H$ ， ③ $E H = D H$ ， ④ $∠ H A B = ∠ H B A$ （）

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 甲、乙两个工程队，甲队修路 $600 m$ 与乙队修路 $800 m$ 所用的时间相等，乙队每天比甲队多修 $20 m$ ．若可列方程 $\frac{600}{x} = \frac{800}{x + 20}$ 表示题中的等量关系，则方程中x表示（）

A、甲队每天修路的长度 B、乙队每天修路的长度 C、甲队修路 $600 m$ 所用的天数 D、乙队修路 $800 m$ 所用的天数

查看试题解析
12. 如图，两个直角三角形重叠在一起，将其中一个沿点 $B$ 到点 $C$ 的方向平移到 $△ D E F$ 的位置， $A B = 10$ ， $D H = 3$ ，平移距离为 $5$ ，则阴影部分的面积为（）

A、 $\frac{125}{3}$ B、 $50$ C、 $\frac{85}{2}$ D、 $75$

查看试题解析

二、填空题（每题3分，共12分）

13. 如图，这是秦始皇陵中的一个兵马俑，兵马俑的眼睛到下巴的距离与头顶到下巴的距离之比约为 $\frac{\sqrt{5} - 1}{2}$ ，其中 $\frac{\sqrt{5} - 1}{2}$ $\frac{1}{2}$ ．（填“ $>$ ”“ $<$ ”或“ $=$ ”）

查看试题解析
14. 已知等腰三角形有两边长分别为2和4，则第三边的长度为．

查看试题解析
15. 关于 $x$ 的分式方程 $\frac{a + 2}{x + 1} = 1$ 无解，则 $a$ 的值为．

查看试题解析
16. 如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3=

查看试题解析

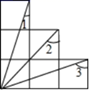
三、解答题（共8题，共72分）

17. 先化简，再求值： $(1 + \frac{1}{x - 2}) \div \frac{x^{2} - x}{x^{2} - 4}$ ，其中 $x = - 7$ ．

查看试题解析
18. 已知：如图，在 $△ A B C$ 中，E是 $A C$ 的中点， $C F ∥ A B$ ，交 $D E$ 的延长线于点F．求证： $D E = F E$ ．

查看试题解析
19.
△ABC在直角坐标系内的位置如图．

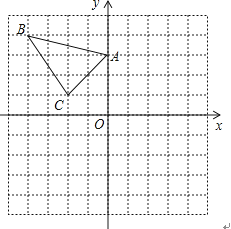(1)、分别写出A、B、C的坐标

(2)、请在这个坐标系内画出△A₁B₁C₁ ，使△A₁B₁C₁与△ABC关于y轴对称，并写出B₁的坐标

查看试题解析
20. 已知一块长为 $7 dm$ ，宽为 $5 dm$ 的长方形木板，如图．

(1)、与这块长方形木板面积相等的正方形木板的边长为______ $dm$ ；

(2)、采用如图的方式，能否在这块木板上截出两个面积分别为 $8 {dm}^{2}$ 和 $18 {dm}^{2}$ 的正方形木板？试说明理由．

查看试题解析
21. 如图，现需要测量该池塘的两端A，B之间的距离，小明同学提出了一种测量方法：如图所示，先在平地上取一个可直接到达A，B的点C，再连接 $A C ， B C$ ，并分别延长 $A C$ 至点D， $B C$ 至点E，使 $D C = A C$ ， $E C = B C$ ，最后量出 $D E$ 的距离就是 $A B$ 的距离．请判断小明的方法其是否可行，并说明理由．

查看试题解析
22. 已知 $a$ ， $b$ ， $c$ 是 $△ A B C$ 的三边长．

(1)、若 $a$ ， $b$ ， $c$ 满足 $|a - b| + {(b - c)}^{2} = 0$ ，试判断 $△ A B C$ 的形状；

(2)、化简： $|a + b - c| + |b - c - a|$

查看试题解析
23. 如图， $A D$ 是 $Δ A B C$ 的高线，且 $B D = \frac{1}{2} A C$ ， $E$ 是 $A C$ 的中点，连结 $B E$ ，取 $B E$ 的中点 $F$ ，连结 $D F$ ，求证： $D F ⊥ B E$ .

查看试题解析
24. 如图1，在等边三角形 $A B C$ 中， $A B = 12$ ．点E，F分别在边 $A C ， B C$ 上，且 $A E = B F = 4$ ，动点 $P$ 从点 $F$ 出发沿射线 $F C$ 运动，以 $E P$ 为边向右侧作等边三角形 $E P M$ ，连接 $C M$ ．

(1)、求证： $△ E F C$ 是等边三角形．

(2)、当点 $P$ 在线段 $F C$ 上运动时，求 $E C ， P C ， C M$ 之间的数量关系．

(3)、如图2，当点 $P$ 在线段 $F C$ 的延长线上运动时，
① $∠ A C M =$ _________ $^{°}$ ；
②如图3作 $C P = C F$ ，再以 $E P$ 为边向右侧作等边三角形 $E P M$ ，连接 $C M$ ，证明： $E P ⊥ C M$ ．

查看试题解析