沪科版数学八年级上册期末质量检测卷(一)
试卷更新日期:2025-12-04 类型:期末考试
一、选择题(每题4分,共40分)
-
1. 下列能准确表示榆中县某个地点位置的是( )A、北纬 B、东经 C、兰州东北方 D、东经 , 北纬2. 下列中华人民共和国全运会会徽图片中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列选项所给条件能画出唯一的是( ).A、 , B、 , , C、 , , D、 , ,4. 在平面直角坐标系中,线段是由线段经过平移得到的,已知点的对应点为 , 点的对应点的坐标为 , 则点的坐标为( )A、 B、 C、 D、5. 如图,是的中线,点和点分别是和的中点,若的面积为 , 则的面积为( )
3. 下列选项所给条件能画出唯一的是( ).A、 , B、 , , C、 , , D、 , ,4. 在平面直角坐标系中,线段是由线段经过平移得到的,已知点的对应点为 , 点的对应点的坐标为 , 则点的坐标为( )A、 B、 C、 D、5. 如图,是的中线,点和点分别是和的中点,若的面积为 , 则的面积为( ) A、6 B、4 C、3 D、26. 为了探究浮力的大小与哪些因素有关,物理实验小组进行了测浮力的实验.如图1,先将一个长方体铁块放在玻璃烧杯上方,再向下缓缓移动,移动过程中记录弹簧测力计的示数F拉力(单位:N)与铁块下降的高度x(单位:cm)之间的关系如图2所示.(温馨提示:当铁块位于水面上方时,;当石块入水后,).下列说法不正确的是( )
A、6 B、4 C、3 D、26. 为了探究浮力的大小与哪些因素有关,物理实验小组进行了测浮力的实验.如图1,先将一个长方体铁块放在玻璃烧杯上方,再向下缓缓移动,移动过程中记录弹簧测力计的示数F拉力(单位:N)与铁块下降的高度x(单位:cm)之间的关系如图2所示.(温馨提示:当铁块位于水面上方时,;当石块入水后,).下列说法不正确的是( )
 A、铁块的高度为4cm B、铁块入水之前,烧杯内水的高度为10cm C、当铁块下降的高度为8cm时,该铁块所受到的浮力为3.25N D、当弹簧测力计的示数为3N时,此时铁块距离烧杯底7. 在同一直角坐标系中,直线与直线可能是( )A、
A、铁块的高度为4cm B、铁块入水之前,烧杯内水的高度为10cm C、当铁块下降的高度为8cm时,该铁块所受到的浮力为3.25N D、当弹簧测力计的示数为3N时,此时铁块距离烧杯底7. 在同一直角坐标系中,直线与直线可能是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,在和中, , . 连接 , 连接并延长交于点 , 若恰好平分 , 则下列结论:①;②;③;④中,正确的是( )
8. 如图,在和中, , . 连接 , 连接并延长交于点 , 若恰好平分 , 则下列结论:①;②;③;④中,正确的是( ) A、①③ B、②④ C、①②③ D、①②③④
A、①③ B、②④ C、①②③ D、①②③④二、填空题(每题5分,共20分)
-
9. 如图, , , 则 .
 10. 如图,在中,于点D,点E是上一点,连接 , , , 若 , , 则的长为 .
10. 如图,在中,于点D,点E是上一点,连接 , , , 若 , , 则的长为 . 11. 定义:若 , 满足 , (为常数),则称点为“好点”.
11. 定义:若 , 满足 , (为常数),则称点为“好点”.(1)若是“好点”,则;
(2)在的范围内,若直线上存在“好点”,则的取值范围为 .
三、解答题(共9题,共90分)
-
12. 如图,直角坐标系中,的顶点都在网格上,其中点坐标为 .
.
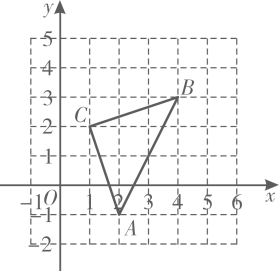 (1)、写出点、的坐标;(2)、将先向左平移个单位长度,再向上平移个单位长度,得到 , 请你画出平移后的 .13. 如图,是的外角的平分线,且交的延长线于点E.
(1)、写出点、的坐标;(2)、将先向左平移个单位长度,再向上平移个单位长度,得到 , 请你画出平移后的 .13. 如图,是的外角的平分线,且交的延长线于点E. (1)、若 , , 求的度数;(2)、直接写出、、三个角之间存在的等量关系.14. 已知一次函数的图象经过点 , 且与y轴的交点的纵坐标为3.求一次函数的解析式.15. 如图,是的高,是的角平分线,是的中线.
(1)、若 , , 求的度数;(2)、直接写出、、三个角之间存在的等量关系.14. 已知一次函数的图象经过点 , 且与y轴的交点的纵坐标为3.求一次函数的解析式.15. 如图,是的高,是的角平分线,是的中线. (1)、若 , , 求的度数;(2)、若 , 与的周长差为3,求的长.16. 如图,直线过点 ,
(1)、若 , , 求的度数;(2)、若 , 与的周长差为3,求的长.16. 如图,直线过点 , (1)、求直线的解析式.(2)、若直线与直线相交于点C,求点C的坐标.(3)、根据图象,写出关于x的不等式的解集.17. 如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.
(1)、求直线的解析式.(2)、若直线与直线相交于点C,求点C的坐标.(3)、根据图象,写出关于x的不等式的解集.17. 如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形. (1)、如图1,是等腰锐角三角形, , 若的角平分线交于点 , 且是的一条特异线,则_______度;(2)、如图2,中, , 线段的垂直平分线交于点D,交于点E,求证:是的一条特异线.(3)、如图3,已知是特异三角形,且 , 为钝角,直接写出所有可能的的度数.18.
(1)、如图1,是等腰锐角三角形, , 若的角平分线交于点 , 且是的一条特异线,则_______度;(2)、如图2,中, , 线段的垂直平分线交于点D,交于点E,求证:是的一条特异线.(3)、如图3,已知是特异三角形,且 , 为钝角,直接写出所有可能的的度数.18. (1)、如图1,在中, , , 是边上的中线,延长到点使 , 连结 , 把 , , 集中在中,利用三角形三边关系可得的取值范围。请写出的取值范围,并说明理由(2)、如图2,在中,是边上的中线,点 , 分别在 , 上,且 , 求证:。小艾同学受到(1)的启发,在解决(2)的问题时,延长到点 , 使……,请你帮她完成证明过程。(3)、如图3,在四边形中,为钝角,为锐角, , , , 点 , 分别在 , 上,且 , 连结 , 试探索线段 , , 之间的数量关系,并加以证明.
(1)、如图1,在中, , , 是边上的中线,延长到点使 , 连结 , 把 , , 集中在中,利用三角形三边关系可得的取值范围。请写出的取值范围,并说明理由(2)、如图2,在中,是边上的中线,点 , 分别在 , 上,且 , 求证:。小艾同学受到(1)的启发,在解决(2)的问题时,延长到点 , 使……,请你帮她完成证明过程。(3)、如图3,在四边形中,为钝角,为锐角, , , , 点 , 分别在 , 上,且 , 连结 , 试探索线段 , , 之间的数量关系,并加以证明.