人教版七(上)第五章 一元一次方程 单元测试培优卷
试卷更新日期:2025-12-03 类型:单元试卷
一、选择题本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. 若 是关于x的一元一次方程, 则m的值为 ( )A、 B、一2 C、2 D、42. 根据等式的性质,下列变形正确的是( )A、如果2x=3,那么x= B、如果x=y,那么x﹣5=5﹣y C、如果x=y,那么﹣2x=﹣2y D、如果x=6,那么x=33. 小明在自学了简单的电脑编程后,设计了如图的程序.若一次性输出的数是 , 则执行了程序后,输入的结果是( )
 A、 B、 C、或 D、或4. 如图,有甲、乙两条数轴.甲数轴上的三点A,B,C所对应的数依次为 , 2,32,乙数轴上的三点D,E,F所对应的数依次为0,x,12.当点A与点D上下对齐时,点B,C恰好分别与点E,F上下对齐时,x的值为( )
A、 B、 C、或 D、或4. 如图,有甲、乙两条数轴.甲数轴上的三点A,B,C所对应的数依次为 , 2,32,乙数轴上的三点D,E,F所对应的数依次为0,x,12.当点A与点D上下对齐时,点B,C恰好分别与点E,F上下对齐时,x的值为( ) A、1 B、2 C、3 D、45. 如图是某月的月历,现用“
A、1 B、2 C、3 D、45. 如图是某月的月历,现用“ ”图形在月历中框出5个数,它们的和为55.不改变“
”图形在月历中框出5个数,它们的和为55.不改变“ ”图形的大小,将“
”图形的大小,将“ ”图形在该月历上移动,所得5个数的和可能是( )
”图形在该月历上移动,所得5个数的和可能是( ) A、40 B、88 C、107 D、1106. 已知关于的方程有整数解,则满足条件的所有整数的和为( )A、 B、2 C、7 D、7. 一批货物用载重为1.5吨的汽车比用载重为4吨的大卡车要多运5次才能运完,若设这批货物共有x吨,则可列出方程为( )A、1.5x-4x=5 B、 C、 D、8. 我国古代的“河图”是由的方格构成的,每个方格内均有.数目(个数为1~9)不同的点图,用实心点“●”表示正数,空心点“○”表示负数.每一行、每一列以及每一条对角线上的三个点图的点数之和均相等.如图,给出了“河图”的部分点图,请你推算出P处所对应的点图是( )
A、40 B、88 C、107 D、1106. 已知关于的方程有整数解,则满足条件的所有整数的和为( )A、 B、2 C、7 D、7. 一批货物用载重为1.5吨的汽车比用载重为4吨的大卡车要多运5次才能运完,若设这批货物共有x吨,则可列出方程为( )A、1.5x-4x=5 B、 C、 D、8. 我国古代的“河图”是由的方格构成的,每个方格内均有.数目(个数为1~9)不同的点图,用实心点“●”表示正数,空心点“○”表示负数.每一行、每一列以及每一条对角线上的三个点图的点数之和均相等.如图,给出了“河图”的部分点图,请你推算出P处所对应的点图是( )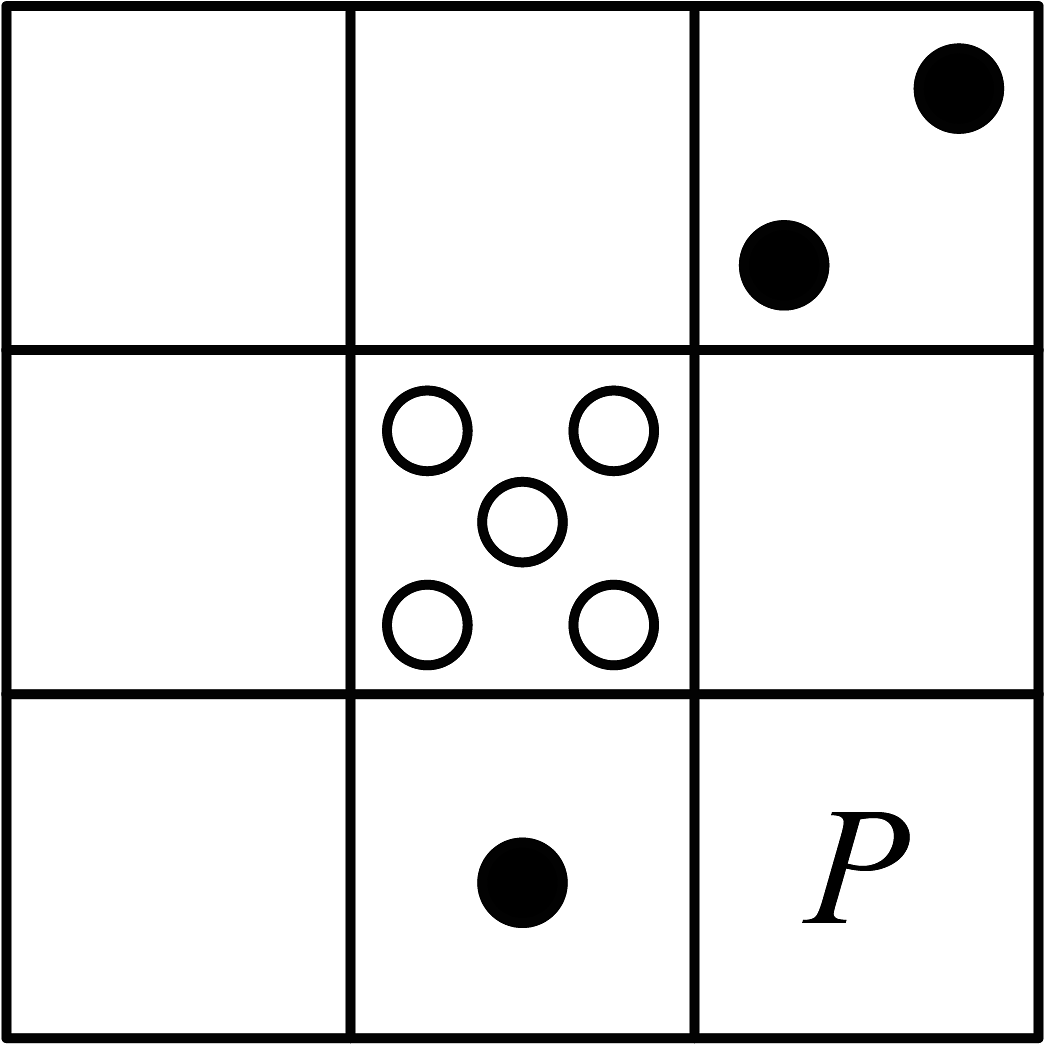 A、
A、 B、
B、 C、
C、 D、
D、 9. 已知正方形甲和长方形乙的周长相等,将它们分别按下图方式放置在同一个大长方形内(两种方式均有重叠).按图1放置时,阴影部分①和②的周长之和为;按图2放置时,阴影部分③和④的周长之和为 . 若 , , 则正方形甲的边长为( )
9. 已知正方形甲和长方形乙的周长相等,将它们分别按下图方式放置在同一个大长方形内(两种方式均有重叠).按图1放置时,阴影部分①和②的周长之和为;按图2放置时,阴影部分③和④的周长之和为 . 若 , , 则正方形甲的边长为( ) A、 B、7 C、7.5 D、810. 规定: , . 例如 , . 下列结论中:①若 , 则;②若 , 则;③能使成立的的值不存在;④式子的最小值是7.其中正确的所有结论是( )A、①②③ B、①②④ C、①③④ D、②③④
A、 B、7 C、7.5 D、810. 规定: , . 例如 , . 下列结论中:①若 , 则;②若 , 则;③能使成立的的值不存在;④式子的最小值是7.其中正确的所有结论是( )A、①②③ B、①②④ C、①③④ D、②③④二、填空题:本大题共5小题,每小题3分,共15分.
-
11. 在数轴上,点A、B表示的数分别是-10和6,点P表示的数为x,点P到点B的距离是点P到点A距离的3倍,则点P表示的数为.12. 若是方程的解,则的值是 .13. 同学们都熟悉“幻方”游戏,现将“幻方”游戏稍作改进变成“幻圆”游戏,将分别填入图中的圆圈内,使横、竖以及内外两个正方形顶点处圈内4个数字之和都相等,则的值为 .
 14. 若关于x的方程没有实数根,则 .15. 甲、乙两人分别从 两地出发, 相向而行, 出发时他们的速度比是 , 他们第一次相遇后,甲的速度提高 ,乙的速度减慢 ,这样,当甲到达 地时,乙离 地还有 26 千米, 两地的距离是千米。
14. 若关于x的方程没有实数根,则 .15. 甲、乙两人分别从 两地出发, 相向而行, 出发时他们的速度比是 , 他们第一次相遇后,甲的速度提高 ,乙的速度减慢 ,这样,当甲到达 地时,乙离 地还有 26 千米, 两地的距离是千米。三、解答题:本大题共8小题,共75分.
-
16. 解方程:(1)、;(2)、 .17. 某中学原计划加工一批校服,现有甲、乙两个工厂加工这批校服,已知甲工厂每天能加工这种校服16件,乙工厂每天加工这种校服24件,且单独加工这批校服甲厂比乙厂要多用20天
(1)求这批校服共有多少件?
(2)为了尽快完成这批校服,若先由甲、乙两工厂按原速度合作一段时间后,甲工厂停工,而乙工厂每天的速度提高25%,乙工厂单独完成剩下的部分,且乙工厂全部工作时间是甲工厂工作时间的2倍还多4天,求乙工厂加工多少天
18. 已知M,N在数轴上,对应的数是 , 点在的右边,且距点4个单位长度,点P,Q是数轴上两个动点.(1)、写出点N所对应的数.(2)、点P到M,N的距离之和是6时,点所对应的数是多少?(3)、如果P,Q分别从点M,N同时出发,均沿数轴向同一方向运动,点每秒走2个单位长度,点每秒走3个单位长度,3秒后,点P,Q之间的距离是多少?19. 规定一种新的运算: , 如果: , 那么求的值.20. 在某市排球“新年杯”比赛中,参赛队伍为12支,比赛采取单循环方式,五局三胜制,积分规则如下,比赛中以或者取胜的球队积分3分,负队积0分;而在比赛中以取胜的球队积2分,负队积1分,前四名队伍积分榜部分信息如下表所示:球队
场次
胜场
负场
总积分
教体
11
11
0
科技
11
10
1
28
工商
11
8
3
公安
11
24
(1)、教体队11场胜场中仅有一场以取胜,则教体队的总积分为_________.(2)、公安队积3分取胜的场次是积2分取胜的场次的3倍,且负场总积分为2分.总积分见上表,求公安队负场的场数.(3)、科技队积3分的胜场数为奇数,则科技队积3分的胜场数为_______场;工商队积3分的胜场数比科技队积3分的胜场数少1场,且工商队负场总积分为3分,则工商队总积分为_______分21. 某品牌饮水机厂生产一种饮水机和饮水机桶,饮水机每台定价350元,饮水机桶每只定价50元,可以同时向客户提供两种优惠方案:方案一:买一台饮水机送一只饮水机桶;
方案二:饮水机和饮水机桶都按定价的90%付款.
现某客户到该饮水机厂购买饮水机30台,饮水机桶x只(x超过30).
(1)、若该客户按方案一购买,求客户需付款(用含x的式子表示);若该客户按方案二购买,求客户需付款(用含x的式子表示);
(2)、若x=40时,通过计算说明此时按哪种方案购买较为合算?(3)、当x=40时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算出所需的钱数.22. 我们知道分数写为小数形式即;反过来,无限循环小数写为分数形式即为 .一般地,任何一个无限循环小数都可以写成一个分数的形式.
例:将化为分数形式.
设 , 由可知, , 所以 , 解得 .
于是得 .
根据以上阅读材料,回答下列问题(以下计算结果都用最简分数表示):
(1)、【理解】 .(2)、【迁移】将化为分数形式,写出推导过程(温馨提示: , 它的循环节有两位).(3)、【创新】若已知 , 则 .