北师大版数学九年级上册期末检测卷(3)[范围:九上全册]
试卷更新日期:2025-12-02 类型:期中考试
一、选择题(每题3分,共24分)
-
1. 如图,直线l1∥l2∥l3 , 直线AB,DE分别交l1 , l2 , l3于点A,B,C和D,E,F,若AB:AC=2:5,EF=15,则DF的长等于( )
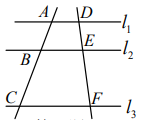 A、18 B、20 C、25 D、302. 用配方法解一元二次方程时,原方程可变形为( )A、 B、 C、 D、3. 如图,在中, , 将绕着点逆时针旋转得到 . 若点的对应点恰好落在上,且 , 则( )
A、18 B、20 C、25 D、302. 用配方法解一元二次方程时,原方程可变形为( )A、 B、 C、 D、3. 如图,在中, , 将绕着点逆时针旋转得到 . 若点的对应点恰好落在上,且 , 则( ) A、 B、 C、 D、4. 某厂1月印科技书籍40万册,第一季度共印140万册,问2月、3月平均每月增长率是多少?设平均增长率为x,则列出下列方程正确的是( )A、(1+x)2=140 B、40(1+x)2=140 C、40+40(1+x)+40(1+x)2=140 D、40+40(1+x)=1405. 如图,在菱形ABCD中,E为AD上一点,F为CB延长线上一点,EF⊥AC于点P,交AB于G,若 则的值为( )
A、 B、 C、 D、4. 某厂1月印科技书籍40万册,第一季度共印140万册,问2月、3月平均每月增长率是多少?设平均增长率为x,则列出下列方程正确的是( )A、(1+x)2=140 B、40(1+x)2=140 C、40+40(1+x)+40(1+x)2=140 D、40+40(1+x)=1405. 如图,在菱形ABCD中,E为AD上一点,F为CB延长线上一点,EF⊥AC于点P,交AB于G,若 则的值为( ) A、 B、 C、 D、6. 如图,在中,点分别在边上,且 . 下列四种说法:
A、 B、 C、 D、6. 如图,在中,点分别在边上,且 . 下列四种说法:①四边形是平行四边形;
②如果 , 那么四边形是矩形;
③如果平分 , 那么四边形是菱形;
④如果 , 且 , 那么四边形是正方形.
其中,正确的有( )
 A、1个 B、2个 C、3个 D、4个7. 如图,在矩形纸片ABCD中, , , 将AB沿AE翻折,使点B落在处,AE为折痕,再将EC沿EF翻折,使点C恰好落在线段上的点处,EF为折痕,连接 . 若 , 则的值为( )
A、1个 B、2个 C、3个 D、4个7. 如图,在矩形纸片ABCD中, , , 将AB沿AE翻折,使点B落在处,AE为折痕,再将EC沿EF翻折,使点C恰好落在线段上的点处,EF为折痕,连接 . 若 , 则的值为( ) A、 B、 C、 D、8. 如图所示,正方形与(其中边 , 分别在 , 轴的正半轴上)的公共顶点在反比例函数的图象上,直线与 , 轴分别相交于点 , . 若这两个正方形的面积之和是 , 且 . 则的值是( )
A、 B、 C、 D、8. 如图所示,正方形与(其中边 , 分别在 , 轴的正半轴上)的公共顶点在反比例函数的图象上,直线与 , 轴分别相交于点 , . 若这两个正方形的面积之和是 , 且 . 则的值是( ) A、5 B、1 C、3 D、2
A、5 B、1 C、3 D、2二、填空题(每题3分,共15分)
-
9. 若关于x的方程(m-4)x|m-2|+2x-5=0是一元二次方程,则m= .10. 如图,将正方形ABCD绕点A逆时针旋转60°得到正方形AEFG,若AB=2,则CF的长度为.
 11. 如图,在平面直角坐标系中,直线与反比例函数的图象交于点A,点B在x轴的负半轴上,连接 . 若 , 的面积为6,则k的值为 .
11. 如图,在平面直角坐标系中,直线与反比例函数的图象交于点A,点B在x轴的负半轴上,连接 . 若 , 的面积为6,则k的值为 . 12. 欧几里得的《几何原本》中记载,形如的方程的图解法如下:如图,以和b为两直角边长作Rt△ABC,再在斜边上截取 , 则AD的长就是所求方程的正根. 若利用以上方法解关于x的一元二次方程时,如果构造后的图形满足AD = 2BD,则m的值为.
12. 欧几里得的《几何原本》中记载,形如的方程的图解法如下:如图,以和b为两直角边长作Rt△ABC,再在斜边上截取 , 则AD的长就是所求方程的正根. 若利用以上方法解关于x的一元二次方程时,如果构造后的图形满足AD = 2BD,则m的值为. 13. 在边长为1的正方形ABCD中,E,F分别为线段AD,DC上的动点,且AE=CF,连接B,F,过E点作EH⊥BF于点H,连接C,H,则CH的最小值为.
13. 在边长为1的正方形ABCD中,E,F分别为线段AD,DC上的动点,且AE=CF,连接B,F,过E点作EH⊥BF于点H,连接C,H,则CH的最小值为.
三、解答题(共7题,共61分)
-
14. 先化简,再求值: , 其中a满足方程 .15. 已知关于的一元二次方程(为常数).(1)、若方程的一个根为1,求的值及方程的另一个根;(2)、求证:不论为何值时,方程总有两个实数根.16. 2023年11月,第一届全国学生(青年)运动会在广西举行,“壮壮”和“美美”作为运动会吉祥物也受到了人们的强烈喜爱.一某超市在今年9月份销售吉祥物毛绒玩具共256个,10月、11月销售量持续走高,在售价不变的基础上,11月份的销售量达到400个.(1)、求10、11这两个月吉祥物毛绒玩具销售量的月平均增长率.(2)、若吉祥物毛绒玩具每个进价25元,原售价为每个40元,该超市在今年12月进行降价促销,经调查发现,若吉祥物毛绒玩具价格在9月的基础上,每个降价1元,月销售量可增加4个,当毛绒玩具每个降价多少元时,出售毛绒玩具在12月份可获利4200元?17. 2024年12月1日在“跃动南马,壮行天下”的口号下第十六届南宁马拉松比赛正式开跑,这场赛事展示了南宁的城市魅力和文化底蕴.为此学校举办了一次南宁历史知识竞赛,并随机抽取部分学生,将竞赛成绩按以下五组进行整理(得分用x表示): , 并绘制出如图的统计图1和图2.
请根据相关信息,解答下列问题:
 (1)、本次竞赛抽取学生的人数为__________,并将条形统计图补充完整.(2)、若“”这一组的数据为:90,96,92,95,93,96,96,95,97,100.则这组数据的众数是__________,中位数是__________.(3)、经过初赛,进入决赛的同学有1名女生和2名男生,现从这三位同学中决出冠亚军,请用列表或画树状图法求冠亚军的两人恰好是一男一女的概率.18. 【定义】连接三角形的一个顶点与对边上任意一点的线段,把这个三角形分割成两个三角形,其中一个是等腰三角形,另一个与原三角形相似,就称这条线段是该三角形的完美分割线。
(1)、本次竞赛抽取学生的人数为__________,并将条形统计图补充完整.(2)、若“”这一组的数据为:90,96,92,95,93,96,96,95,97,100.则这组数据的众数是__________,中位数是__________.(3)、经过初赛,进入决赛的同学有1名女生和2名男生,现从这三位同学中决出冠亚军,请用列表或画树状图法求冠亚军的两人恰好是一男一女的概率.18. 【定义】连接三角形的一个顶点与对边上任意一点的线段,把这个三角形分割成两个三角形,其中一个是等腰三角形,另一个与原三角形相似,就称这条线段是该三角形的完美分割线。
 (1)、【应用】
(1)、【应用】如图1,△ABC中,AC=3,AB=4,BC=2,D是AB上一点,BD=1,求证:CD是△ABC的完美分割线;
(2)、如图2,菱形ABCD中,AB=4,点E是边CD的中点,点F是边BC上一点,连接AF交线段BE于G,若BG是△ABF的完美分割线,且AB=AG,求FG的长;(3)、如图3,矩形ABCD中,点O是DB的中点,E为射线DA上的动点,连接EO并延长交射线BC于F,G是射线OB上一点,∠GFO=∠DFO,若GO是△EGF的完美分割线,请直接写出的值。19. 请认真阅读材料材料1:法国数学家弗朗索瓦·韦达在著作《论方程的识别与订正》中提出一元二次方程的两根有如下的关系:;
材料2:如果实数m、n满足、 , 且 , 则可利用根的定义构造一元二次方程 , 将m、n看作是此方程的两个不相等的实数根;
材料3:如果实数m、n满足、 , 且 , 则可利用根的定义构造一元二次方程 , 将、看作是此方程的两个不相等的实数根;
材料4:如果实数m、n满足、 , 则可利用韦达定理构造一元二次方程 , 将m、n看作是此方程的两个实数根,且此方程一定有m、n两个实数根。
请根据上述材料解决下面问题:
(1)、已知实数m、n满足、 , 求的值.(2)、已知实数p、q满足、 , 且 , 求的值.(3)、已知实数a、b、c满足、 , 求c的最大值.