华东师大版数学八年级上册期末检测卷(三)
试卷更新日期:2025-12-02 类型:期末考试
一、选择题(每题5分,共60分)
-
1. 在实数中,无理数有( )个A、2 B、3 C、4 D、52. 将下列长度的三根木棒首尾顺次连接,能组成直角三角形的是( )A、2、3、4 B、4、5、6 C、5、11、12 D、8、15、173. 9的算术平方根是( )A、 ﹣3 B、±3 C、3 D、4. 下列各式的变形中,是因式分解的是( )A、3x(2x+5)=6x2+15x B、2x2-x+1=x(2x-1)+1 C、x2-xy=x(x-y) D、(x+1)(x+3)=x2+4x+35. 下列命题的逆命题是真命题的是( )A、全等三角形的对应角相等 B、如果两个有理数相等,那么它们的平方相等 C、如果两个角是对顶角,那么这两个角相等 D、两直线平行,同位角相等6. 计算的结果为( )A、3 B、 C、 D、7. 如图,中,于点D,若 , 则( )
 A、 B、 C、 D、8. 一辆装满货物,宽为米的卡车,欲通过如图所示的隧道(隧道下方为长方形,上方为半圆形拱门),则卡车的外形不得高于( )
A、 B、 C、 D、8. 一辆装满货物,宽为米的卡车,欲通过如图所示的隧道(隧道下方为长方形,上方为半圆形拱门),则卡车的外形不得高于( ) A、米 B、米 C、米 D、米9. 已知 , , 则的值为( )A、72 B、 C、 D、10. 在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,根据图中标示的各点位置,与△ABC全等的是( )
A、米 B、米 C、米 D、米9. 已知 , , 则的值为( )A、72 B、 C、 D、10. 在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,根据图中标示的各点位置,与△ABC全等的是( ) A、△ACF B、△ACE C、△ABD D、△CEF11. 如图,为了庆祝“五•一”,学校准备在教学大厅的圆柱体柱子上贴彩带,已知柱子的底面周长为 , 高为 . 如果要求彩带从柱子底端的处均匀地绕柱子圈后到达柱子顶端的处(线段与地面垂直),那么应购买彩带的长度为( )
A、△ACF B、△ACE C、△ABD D、△CEF11. 如图,为了庆祝“五•一”,学校准备在教学大厅的圆柱体柱子上贴彩带,已知柱子的底面周长为 , 高为 . 如果要求彩带从柱子底端的处均匀地绕柱子圈后到达柱子顶端的处(线段与地面垂直),那么应购买彩带的长度为( ) A、 B、 C、 D、12. 已知a , b , c为△ABC三边,且满足 , 则△ABC是( )A、直角三角形 B、等边三角形 C、等腰三角形 D、不能确定
A、 B、 C、 D、12. 已知a , b , c为△ABC三边,且满足 , 则△ABC是( )A、直角三角形 B、等边三角形 C、等腰三角形 D、不能确定二、填空题(每题5分,共20分)
-
13. 如果 , 那么.14. 已知等腰三角形的一内角度数为 , 则它的底角的度数是 .15. 如图,点是正方形内一点,连接 , 且 , 以为斜边在下方作Rt , 且 , 若 , 则正方形的面积为 .
 16. 如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E.若S△ABC=7,DE=2,AB=4,则AC的长是
16. 如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E.若S△ABC=7,DE=2,AB=4,则AC的长是
三、解答题(共8题,共70分)
-
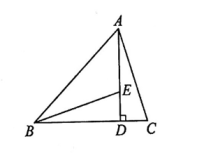
17. 分解因式:(1)、(2)、18. 如图,已知AD是△ABC的边BC上的高,E为AD上一点,且BE=AC,DE=DC.
求证:∠DBE=∠DAC.
 19. “油纸伞”是汉族古老的传统工艺品之一(如图1),其制作工艺十分巧妙.如图2,伞圈D沿着伞柄AP滑动时,总有伞骨AB=AC,BD=CD.问:伞柄AP是否始终平分同一平面内两条伞骨所成的∠BAC?请说明理由.
19. “油纸伞”是汉族古老的传统工艺品之一(如图1),其制作工艺十分巧妙.如图2,伞圈D沿着伞柄AP滑动时,总有伞骨AB=AC,BD=CD.问:伞柄AP是否始终平分同一平面内两条伞骨所成的∠BAC?请说明理由.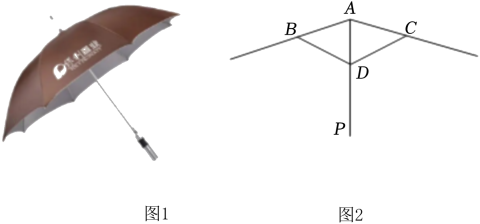 20. 已知:如图,角平分线与的垂直平分线交于点D, , , 垂足分别为E、F.
20. 已知:如图,角平分线与的垂直平分线交于点D, , , 垂足分别为E、F. (1)、求证:;(2)、若 , , 求的长.21. 巴川中学STEAM创新教育学部为提高学生的安全意识和安全技能,组织七、八年级学生进入区消防支队进行了实地学习和体验,并在学习结束后开展了一次消防知识竞赛.成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为10分、9分、8分、7分.学校分别从七、八年级各抽取25名学生的竞赛成绩整理并绘制成如下统计图表,请根据提供的信息解答下列问题:
(1)、求证:;(2)、若 , , 求的长.21. 巴川中学STEAM创新教育学部为提高学生的安全意识和安全技能,组织七、八年级学生进入区消防支队进行了实地学习和体验,并在学习结束后开展了一次消防知识竞赛.成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为10分、9分、8分、7分.学校分别从七、八年级各抽取25名学生的竞赛成绩整理并绘制成如下统计图表,请根据提供的信息解答下列问题:年级
平均分
中位数
众数
方差
七年级
a
9
八年级
8
b
 (1)、根据以上信息可以求出:a= , b= , 并把七年级竞赛成绩统计图补充完整;(2)、依据数据分析表,你认为七年级和八年级哪个年级的成绩更好,并说明理由;(3)、若STEAM创新教育学部七、八年级共有800人参加本次知识竞赛,且规定9分及以上的成绩为优秀,请估计该学部七、八年级参加本次知识竞赛的学生中成绩为优秀的学生共有多少人?22. 如图,台风“海葵”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,经测量,距离台风中心260km及以内的地区会受到影响.
(1)、根据以上信息可以求出:a= , b= , 并把七年级竞赛成绩统计图补充完整;(2)、依据数据分析表,你认为七年级和八年级哪个年级的成绩更好,并说明理由;(3)、若STEAM创新教育学部七、八年级共有800人参加本次知识竞赛,且规定9分及以上的成绩为优秀,请估计该学部七、八年级参加本次知识竞赛的学生中成绩为优秀的学生共有多少人?22. 如图,台风“海葵”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,经测量,距离台风中心260km及以内的地区会受到影响. (1)、海港C受台风影响吗?为什么?(2)、若台风中心的移动速度为25千米/时,则台风影响该海港持续的时间有多长?23. 阅读材料:学习了无理数后,某数学兴趣小组开展了一次探究活动:估算的近似值.
(1)、海港C受台风影响吗?为什么?(2)、若台风中心的移动速度为25千米/时,则台风影响该海港持续的时间有多长?23. 阅读材料:学习了无理数后,某数学兴趣小组开展了一次探究活动:估算的近似值.小明的方法:
∵ , 设 ,
∴ . ∴ .
∴ , 解得 . ∴ .
(上述方法中使用了完全平方公式: , 下面可参考使用)问题:
(1)、请你依照小明的方法,估算的值(结果保留两位小数);(2)、请结合上述具体实例,概括出估算的公式:已知非负整数a、b、 , 且 , 估计的值(用含a、b的代数式表示);(3)、请用(2)中的结论估算的近似值.24. 【探究与证明】【新定义】顶角相等且顶角顶点重合的两个等腰三角形互为“兄弟三角形”.
 (1)、如图1,和互为“兄弟三角形”,点为重合的顶角顶点.则(填“>”、“<”或“=”);(2)、如图2,和互为“兄弟三角形”,点为重合的顶角顶点,连接、 , 试猜想线段、的大小关系,并证明你的结论;(3)、如图3,和互为“兄弟三角形”,点为重合的顶角顶点,点、点均在外,连接、交于点 , 连接 , 求证:平分.
(1)、如图1,和互为“兄弟三角形”,点为重合的顶角顶点.则(填“>”、“<”或“=”);(2)、如图2,和互为“兄弟三角形”,点为重合的顶角顶点,连接、 , 试猜想线段、的大小关系,并证明你的结论;(3)、如图3,和互为“兄弟三角形”,点为重合的顶角顶点,点、点均在外,连接、交于点 , 连接 , 求证:平分.