华东师大版数学八年级上册期末检测卷(一)
试卷更新日期:2025-12-02 类型:期末考试
一、选择题(每题5分,共60分)
-
1. 在四个实数中,小于的实数是( )A、1 B、0 C、 D、2. 将下列长度的三根木棒首尾顺次连接,能组成直角三角形的是( )A、2、3、4 B、4、5、6 C、5、11、12 D、8、15、173. 下列各数: , ﹣ , , , , 2.1010010001……(相邻两个1之间的0的个数逐次加1),3.1234567891011……(小数部分由相继的正整数组成)中,无理数有( )A、2个 B、3个 C、4个 D、5个4. 下列各式从左到右的变形,属于因式分解的是( )A、 B、 C、 D、5. 如图,若 , 则添加下列一个条件后,仍无法判定的是( )
 A、 B、 C、 D、6. 下列命题的逆命题是真命题的是( )A、全等三角形的对应角相等 B、如果两个有理数相等,那么它们的平方相等 C、如果两个角是对顶角,那么这两个角相等 D、两直线平行,同位角相等7. 体育强则中国强,国运兴则体育兴.在2024年巴黎奥运会上,中国体育健儿发挥出色,共获得40块金牌、27块银牌和24块铜牌.要想清楚地表示出中国体育代表团获得各类奖牌数量与奖牌总数之间的关系,适合绘制( )A、扇形统计图 B、折线统计图 C、条形统计图 D、以上统计图均可以8. 的三边分别是 , , , 其中能构成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,9. 如图,AC⊥BD,∠1=∠2,∠D=35°,则∠BAD的度数是( ).
A、 B、 C、 D、6. 下列命题的逆命题是真命题的是( )A、全等三角形的对应角相等 B、如果两个有理数相等,那么它们的平方相等 C、如果两个角是对顶角,那么这两个角相等 D、两直线平行,同位角相等7. 体育强则中国强,国运兴则体育兴.在2024年巴黎奥运会上,中国体育健儿发挥出色,共获得40块金牌、27块银牌和24块铜牌.要想清楚地表示出中国体育代表团获得各类奖牌数量与奖牌总数之间的关系,适合绘制( )A、扇形统计图 B、折线统计图 C、条形统计图 D、以上统计图均可以8. 的三边分别是 , , , 其中能构成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,9. 如图,AC⊥BD,∠1=∠2,∠D=35°,则∠BAD的度数是( ).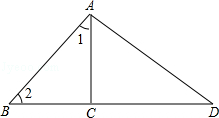 A、 B、 C、 D、10. 若 , 则a的值为( )A、 B、 C、4 D、±411. 若 , , 则的所有可能值为( )A、0 B、6 C、或6 D、0或12. 如图,中,与的平分线交于点F,过点F作交于点D,交于点E,那么下列结论,其中不正确的有( )
A、 B、 C、 D、10. 若 , 则a的值为( )A、 B、 C、4 D、±411. 若 , , 则的所有可能值为( )A、0 B、6 C、或6 D、0或12. 如图,中,与的平分线交于点F,过点F作交于点D,交于点E,那么下列结论,其中不正确的有( ) A、是等腰三角形 B、 C、若 , 则 D、
A、是等腰三角形 B、 C、若 , 则 D、二、填空题(每题5分,共20分)
-
13. , 则的值为 .14. 如图所示,数轴上的点表示的实数为 , 以点为圆心,为半径画弧交数轴于点 , 则点表示的数是 .
 15. 若 , 则 .16. 如图,在中,按以下步骤作图:①以点为圆心,任意长为半径画弧,与边分别交于点;②分别以为圆心,大于的长为半径画弧,两弧在内交于点;③作射线 , 交于点;④过点作 , 垂足为点 . 若的面积为9, , , 则的长为 .
15. 若 , 则 .16. 如图,在中,按以下步骤作图:①以点为圆心,任意长为半径画弧,与边分别交于点;②分别以为圆心,大于的长为半径画弧,两弧在内交于点;③作射线 , 交于点;④过点作 , 垂足为点 . 若的面积为9, , , 则的长为 .
三、解答题(共8题,共70分)
-
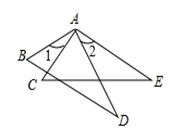
17. 因式分解:(1)、;(2)、 .18. 已知:如图,AB=AC , AD=AE , ∠1=∠2.求证:△ABD≌△ACE .
 19. 已知 , .(1)、求的值.(2)、求的值.20. 如图,相交于点O , , , 连接 , 求证: .
19. 已知 , .(1)、求的值.(2)、求的值.20. 如图,相交于点O , , , 连接 , 求证: . 21. 如图,是由边长为 1 的正方形构成的 的网格图, 的顶点都在格点上.
21. 如图,是由边长为 1 的正方形构成的 的网格图, 的顶点都在格点上. (1)、判断是否为等腰三角形_____.(填是或否),并直接写出的面积为_____;(2)、命题 “腰长相等的两个等腰三角形是全等三角形”是真命题还是假命题?如果是假命题,请在图中再画一个顶点是格点的三角形说明; 若是真命题,请进行证明.22. 在数学活动课上,同学们用边长为 , 的两个正方形 , (如图1)进行摆放,其中 . 现有两种摆放方式:方式一,如图2,将正方形放在正方形内部;方式二,如图3,将正方形 , 并列放置在边长为的正方形内部.若记图1中正方形 , 的面积之和为 , 记图2,图3中阴影部分的面积分别为 , , 解答下列问题:
(1)、判断是否为等腰三角形_____.(填是或否),并直接写出的面积为_____;(2)、命题 “腰长相等的两个等腰三角形是全等三角形”是真命题还是假命题?如果是假命题,请在图中再画一个顶点是格点的三角形说明; 若是真命题,请进行证明.22. 在数学活动课上,同学们用边长为 , 的两个正方形 , (如图1)进行摆放,其中 . 现有两种摆放方式:方式一,如图2,将正方形放在正方形内部;方式二,如图3,将正方形 , 并列放置在边长为的正方形内部.若记图1中正方形 , 的面积之和为 , 记图2,图3中阴影部分的面积分别为 , , 解答下列问题: (1)、用 , 的代数式表示;(2)、若的三边长分别为 , , . 试猜想是哪一类三角形,并证明你的猜想;(3)、已知直角三角形的两边长为 , , 且 , 为整数,当时,求直角三角形第三边的长.23. “一线三等角”模型是平面几何图形中的重要模型之一,“一线三等角”指的是图形中出现同一条直线上有3个相等的情况,在学习过程中,我们发现“一线三等角”模型的出现,还经常会伴随着出现全等三角形.
(1)、用 , 的代数式表示;(2)、若的三边长分别为 , , . 试猜想是哪一类三角形,并证明你的猜想;(3)、已知直角三角形的两边长为 , , 且 , 为整数,当时,求直角三角形第三边的长.23. “一线三等角”模型是平面几何图形中的重要模型之一,“一线三等角”指的是图形中出现同一条直线上有3个相等的情况,在学习过程中,我们发现“一线三等角”模型的出现,还经常会伴随着出现全等三角形.根据对材料的理解解决以下问题∶
 (1)、如图1, , . 猜想 , , 之间的关系:(2)、如图2,将(1)中条件改为 , , 请问(1)中的结论是否成立?若成立,请给出证明;若不成立,请说明理由;(3)、如图3,在中,点为上一点, , , , , 请直接写出的长.
(1)、如图1, , . 猜想 , , 之间的关系:(2)、如图2,将(1)中条件改为 , , 请问(1)中的结论是否成立?若成立,请给出证明;若不成立,请说明理由;(3)、如图3,在中,点为上一点, , , , , 请直接写出的长.