华东师大版数学七年级上册期末检测卷（二）

试卷更新日期：2025-12-02 类型：期末考试

进入出卷网下载

一、选择题（每题5分，共60分）

1. 下列几何体中，从上面观察得到的平面图形是三角形的是（）

A、 B、 C、 D、

查看试题解析
2. 冰箱冷藏室的温度零上 $3 ℃$ ，记作 $+ 3 ℃$ ，冷冻室的温度零下 $8 ℃$ ，应记作（）

A、 $8 ℃$ B、 $- 8 ℃$ C、 $5 ℃$ D、 $- 5 ℃$

查看试题解析
3. 下列各数： $4^{3}, {(- \frac{1}{3})}^{5}, - 3^{2}, 0$ ，在数轴上所对应的点在原点右边的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 下列计算中，结果正确的是（）．

A、 $3 x^{3} - 2 x^{3} = 1$ B、 $2 x^{2} + 4 x^{2} = 6 x^{4}$ C、 $3 x^{2} y - 3 y x^{2} = 0$ D、 $3 x + y = 3 x y$

查看试题解析
5. 下列说法中，正确的是（）

A、一个有理数，不是整数就是分数 B、 $- \frac{3 π a b c}{2}$ 系数是 $- \frac{3}{2}$ 次数是4 C、一个数的绝对值一定是正数 D、任何数都有倒数

查看试题解析
6. 如图，高速公路在建设过程中，通常要开挖隧道穿过山体，把道路取直以缩短路程，其中最能解释这一做法的数学知识是（）

A、两点之间，线段最短 B、两点确定一条直线 C、平面内经过一点有无数条直线 D、连结两点的线段的长度叫作这两点间的距离

查看试题解析
7. 如果多项式 $(- a - 1) x^{5} - \frac{2}{3} x^{b} + x - 9$ 是关于 $x$ 的三次三项式，那么 $\frac{a}{b}$ 的值为（）

A、 $- 3$ B、 $- \frac{1}{3}$ C、 $3$ D、 $\frac{1}{3}$

查看试题解析
8. 将一副直角三角板按如图所示各位置摆放，其中∠a与∠β一定互余的是（）

A、 B、 C、 D、

查看试题解析
9. 下列每个平面图形均由6个大小相同的小正方形组成，其中不能折叠成正方体的是（）

A、 B、 C、 D、

查看试题解析
10. 多项式 $6 a b - 9 + k a b$ 合并同类项后得 $- 9$ ，则 $k$ 的值为（）

A、 $- 6$ B、 $- 1$ C、0 D、6

查看试题解析
11. 大约从 20 世纪 50 年代开始，许多国家流传着这样一个数学猜想，其原理如下图数值转换器。若开始输入 $x$ 的值是 5 ，则第 1 次输出的结果是 16 ，第 2 次输出的结果是 8 ，第 3 次输出的结果是 4 ．依次继续下去，第 2025 次输出的结果是（）

A、1
B、2
C、3 D、4

查看试题解析
12. 如图，长方形ABCD 的边长AB=DC=x，AD=BC=y。在长方形ABCD内，将一张边长为a和两张边长为b(a>b)的正方形纸片按图1，图2两种方式放置，长方形中未被这三张正方形纸片覆盖的部分用阴影表示，设图2中阴影部分的周长与图1中阴影部分的周长的差为L，若要知道L的值，只要测量图中哪条线段的长( )

A、a B、b C、x D、y

查看试题解析

二、填空题（每题5分，共20分

13. 若 $3 x - 5$ 与 $- 2 x$ 互为相反数，则 $x =$ ．

查看试题解析
14. 如图，在灯塔O处观测到轮船A位于北偏西 $54 °$ 的方向，同时轮船B在南偏东 $15 °$ 的方向，那么 $∠ A O B$ 的度数为．

查看试题解析
15. 对非零有理数 $a$ ， $b$ 定义一种运算 $\otimes$ ，其规则是： $a \otimes b = - \frac{1}{b} \div \frac{1}{a}$ ，则 $(- 3) \otimes (- 2) =$ ．

查看试题解析
16. 如图，两根木条的长度分别为 $9 c m$ 和 $14 c m$ ，在它们的中点处各打一个小孔M ， N（木条的厚度，宽度以及小孔大小均忽略不计）．将这两根木条的一端重合并放置在同一条直线上，则两小孔间的距离 $M N =$ $c m$ ．

查看试题解析

三、解答题（共8题，共70分）

17. 计算：

(1)、 $- 1^{2} - |1 - {(- 2)}^{3}| + (- \frac{5}{3}) + \frac{10}{9}$ ；

(2)、 $(1 \frac{1}{2} - \frac{2}{5} - \frac{3}{10}) \div (- \frac{3}{5})$ ．

查看试题解析
18. 如图，点 $O$ 在直线 $A B$ 上，射线 $O C, O D, O E$ 在直线 $A B$ 的同一侧， $∠ 1$ 与 $∠ 2$ 互余， $O E$ 平分 $∠ C O D$ ．

(1)、求 $∠ D O E$ 的度数．

(2)、求 $∠ B O E + ∠ D O A$ 的度数．

查看试题解析
19. 请你先认真阅读材料：
计算： $(- \frac{1}{30}) \div (\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5})$ ．
解：原式的倒数是： $(\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5}) \div (- \frac{1}{30})$
$= (\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5}) \times (- 30)$
$= \frac{2}{3} \times (- 30) - \frac{1}{10} \times (- 30) + \frac{1}{6} \times (- 30) - \frac{2}{5} \times (- 30)$
$= - 20 - (- 3) + (- 5) - (- 12)$
$= - 10$
故原式等于 $- \frac{1}{10}$ ．
根据你对所提供材料的理解，选择合适的方法计算：
$(- \frac{1}{42}) \div (\frac{1}{6} - \frac{3}{14} + \frac{2}{3} - \frac{2}{7})$ ．

查看试题解析
20. 小明早晨跑步，他从自己家出发，向东跑了 $2 km$ 到达小彬家，继续向东跑了 $1.5 km$ 到达小红家，然后又向西跑了 $4.5 km$ 到达学校，最后又向东跑回到自己家．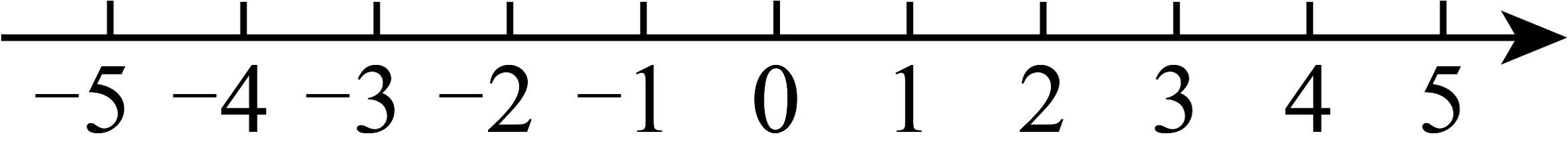

(1)、以小明家为原点，向东为正方向，用1个单位长度表示 $1 km$ ，在图中的数轴上，分别用点A表示出小彬家，用点 $B$ 表示出小红家，用点 $C$ 表示出学校的位置；

(2)、求小彬家与学校之间的距离；

(3)、如果小明跑步的速度是 $250 m / min$ ，那么小明跑步一共用了多长时间？

查看试题解析
21. 已知：如图， $G D ∥ C A$ ， $∠ 1 + ∠ 2 = 180 °$ ．

(1)、判断 $C D$ 与 $E F$ 的位置关系，并说明理由．

(2)、若 $D G$ 平分 $∠ C D B$ ， $∠ A C D = 40 °$ ，求 $∠ E F B$ 的度数．

查看试题解析
22. 学习了绝对值的概念后，我们可以认为：一个非负数的绝对值等于它本身，负数的绝对值等于它的相反数，即当a＜0时，|a|＝﹣a ，根据以上阅读完成下面的问题：

(1)、 $| 3.14 - π | =$ ；

(2)、如果有理数 $a < b$ ，则 $| a - b | =$ ；

(3)、请利用你探究的结论计算下面式子：
$| \frac{1}{2} - 1 | + | \frac{1}{3} - \frac{1}{2} | + | \frac{1}{4} - \frac{1}{3} | + ⋯ + | \frac{1}{2022} - \frac{1}{2021} | + | \frac{1}{2023} - \frac{1}{2022} |$

(4)、如图，数轴上有a、b、c三点，化简 $| a | + | a + b | - 2 | b - c |$ .

查看试题解析
23.

(1)、如图1，已知点M ， N是线段CD上两点，且 $C D = 6 C M = 4 D N$ ，点E和点F分别是线段CN和线段DM的中点．若线段 $C D = 24 c m$ ，分别求线段 $C M$ ， $D N$ ， $E F$ 的长；

(2)、已知OM ， ON是从 $∠ C O D$ 的顶点发出的两条射线， $∠ C O D = 6 ∠ C O M$ 且 $∠ C O D = 144 °$ ，射线OE和射线OF分别平分 $∠ C O N$ ， $∠ D O M$ ．
①如图2，若OM ， ON均为 $∠ C O N$ 内的两条射线，且 $∠ C O D = 4 ∠ D O N$ ，求 $∠ E O F$ 的度数；
②如图3，若OM为 $∠ C O D$ 外的一条射线，且 $∠ E O F = 18 °$ ，则 $∠ D O N =$ ▲ ．

查看试题解析