华东师大版数学七年级上册期末检测卷(三)
试卷更新日期:2025-12-02 类型:期末考试
一、选择题(每题5分,共60分)
-
1. 几何体是由曲面或平面围成的,下列几何体面数最少的是( )A、
 B、
B、 C、
C、 D、
D、 2. ﹣3的相反数是( )A、 B、 C、 D、3. 下列各组的两个数中,运算后结果相等的是( )A、与 B、与 C、与 D、与4. 若与是同类项,则有( )A、m=1,n=2 B、m=1,n=-1 C、m=0,n=-1 D、m=0,n=25. 一个正方体的相对的表面上所标的数都是互为相反数的两个数,如图是这个正方体的表面展开图,那么图中x的值是( )
2. ﹣3的相反数是( )A、 B、 C、 D、3. 下列各组的两个数中,运算后结果相等的是( )A、与 B、与 C、与 D、与4. 若与是同类项,则有( )A、m=1,n=2 B、m=1,n=-1 C、m=0,n=-1 D、m=0,n=25. 一个正方体的相对的表面上所标的数都是互为相反数的两个数,如图是这个正方体的表面展开图,那么图中x的值是( ) A、-8 B、-3 C、-2 D、36. 已知 , 则的补角等于( )A、 B、 C、 D、7. 如图,点A、B、C不在一条直线上,先作直线BC , 再过点A作射线AD与线段BC交于点D , 下列正确的作图是( )
A、-8 B、-3 C、-2 D、36. 已知 , 则的补角等于( )A、 B、 C、 D、7. 如图,点A、B、C不在一条直线上,先作直线BC , 再过点A作射线AD与线段BC交于点D , 下列正确的作图是( ) A、
A、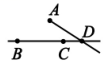 B、
B、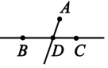 C、
C、 D、
D、 8. 点 , , 在同一直线上,已知 , , 则线段的长是( )A、2cm B、3cm C、2cm或5cm D、3cm或5cm9. 已知 , , 且 , 则的值等于( )A、或 B、或 C、或 D、或10. 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳记数”.一位书生坚持每天五更起床读书,为了勉励自己,他用“结绳记数”的方法来记录自己读书的天数,如图1是他从右到左依次排列的绳子上打结,满七进一,表示的天数为66天.按同样的方法,图2表示的天数是( )
8. 点 , , 在同一直线上,已知 , , 则线段的长是( )A、2cm B、3cm C、2cm或5cm D、3cm或5cm9. 已知 , , 且 , 则的值等于( )A、或 B、或 C、或 D、或10. 我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳记数”.一位书生坚持每天五更起床读书,为了勉励自己,他用“结绳记数”的方法来记录自己读书的天数,如图1是他从右到左依次排列的绳子上打结,满七进一,表示的天数为66天.按同样的方法,图2表示的天数是( ) A、72 B、343 C、366 D、103211. 有理数a,b,c,d在数轴上的对应点的位置如图所示.若|a-c|=10,|a-d|=12,|b-d|=9,则|b-c|的值是( ).
A、72 B、343 C、366 D、103211. 有理数a,b,c,d在数轴上的对应点的位置如图所示.若|a-c|=10,|a-d|=12,|b-d|=9,则|b-c|的值是( ). A、5 B、6 C、7 D、1012. 如图,大长方形ABCD是由正方形一、二、三、五和小长方形四拼成的,且正方形一、二、三的边长分别为a , b , c(),有以下结论:①;②小长方形四的宽是;③;④大长方形ABCD的周长为其中正确的结论有( )
A、5 B、6 C、7 D、1012. 如图,大长方形ABCD是由正方形一、二、三、五和小长方形四拼成的,且正方形一、二、三的边长分别为a , b , c(),有以下结论:①;②小长方形四的宽是;③;④大长方形ABCD的周长为其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每题5分,共20分)
-
13. 如图,在灯塔O处观测到轮船A位于北偏西的方向,同时轮船B在南偏东的方向,那么的度数为 .
 14. 计算: .15. 若关于的两个多项式与的和为三次三项式,则的值为 .16. 如图,点O在直线AB上,从点O引出射线OC,其中射线OD平分∠AOC,射线OE平分∠BOC,下列结论:
14. 计算: .15. 若关于的两个多项式与的和为三次三项式,则的值为 .16. 如图,点O在直线AB上,从点O引出射线OC,其中射线OD平分∠AOC,射线OE平分∠BOC,下列结论:
①∠DOE=90°;
②∠COE与∠AOE互补;
③若OC平分∠BOD,别∠AOE=150°;
④∠BOE的余角可表示为 .
其中正确的是 . (只填序号)
三、解答题(共8题,共70分)
-
17. 计算:(1)、 ;(2)、 .18. 计算:(1)、;(2)、 .19. 贵阳地铁3号线自运营以来,为市民和游客带来了前所未有的便捷体验.如图是3号线部分站点示意图,小红作为地铁志愿者,从茶店站开始乘坐地铁做引导服务,最后她在A站结束服务活动.若规定向花果园站方向为正,则小红当天乘地铁的站数按先后顺序依次记录如下(单位:站): , , , , , .
 (1)、请通过计算说明A站是哪一站?(2)、假设相邻两站之间的平均距离为1.5 , 求这次小红志愿服务期间乘坐地铁的总路程为多少千米?20. 某建筑物的地面结构如图所示(图中各图形均为长方形或正方形),请根据图中的数据(单位:米),解答下列问题:
(1)、请通过计算说明A站是哪一站?(2)、假设相邻两站之间的平均距离为1.5 , 求这次小红志愿服务期间乘坐地铁的总路程为多少千米?20. 某建筑物的地面结构如图所示(图中各图形均为长方形或正方形),请根据图中的数据(单位:米),解答下列问题: (1)、用含 , 的代数式表示阴影面积;(2)、图中阴影部分需要铺设地砖,铺地砖每平方米的平均费用为100元,若 , , 则铺地砖的总费用为多少元?21. 小红做一道数学题:“两个多项式 , 已知为 , 试求的值”时.小红误将看成 , 结果答案为(计算过程正确).(1)、试求的正确结果;(2)、当时,求的值.22. 如图,已知直线 l与直线 AB,CD 分别交于点 E,F, 于点 G, 与 互余.
(1)、用含 , 的代数式表示阴影面积;(2)、图中阴影部分需要铺设地砖,铺地砖每平方米的平均费用为100元,若 , , 则铺地砖的总费用为多少元?21. 小红做一道数学题:“两个多项式 , 已知为 , 试求的值”时.小红误将看成 , 结果答案为(计算过程正确).(1)、试求的正确结果;(2)、当时,求的值.22. 如图,已知直线 l与直线 AB,CD 分别交于点 E,F, 于点 G, 与 互余.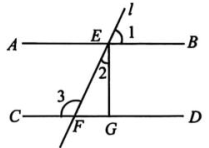 (1)、 判断直线 AB 与 CD 的位置关系,并说明理由.(2)、 若 , 求 的度数.23. 如图,与互为补角,与互为余角.
(1)、 判断直线 AB 与 CD 的位置关系,并说明理由.(2)、 若 , 求 的度数.23. 如图,与互为补角,与互为余角. (1)、若 , 求的大小;(2)、若 .
(1)、若 , 求的大小;(2)、若 .①求的度数;
②如果平分 , 求的度数.
24. 对于数轴上的一点和线段(点不与点、点重合),给出如下定义:若点满足 , 则称点为线段的“偏移对称点”.已知数轴上、两点表示的数分别是、 , 且 .(1)、当时,①若点表示的数分别为 , 则点是线段B的“偏移对称点”;
②已知点为数轴原点,点是数轴负半轴上的一个动点,若线段上存在一点 , 使得点是线段的“偏移对称点”,则线段长度的最小值为______;
(2)、对于数轴上的任意两点、(点在点的左侧),且 , 总存在线段 , 使得线段上的任意一点都是线段的“偏移对称点”,求的取值范围.