天津市北京师范大学天津生态城附属学校2025-2026学年高三上学期期中数学测试卷
试卷更新日期:2025-11-15 类型:期中考试
一、单选题(本大题共9小题,共45分.在每小题列出的选项中,选出符合题目的一项)
-
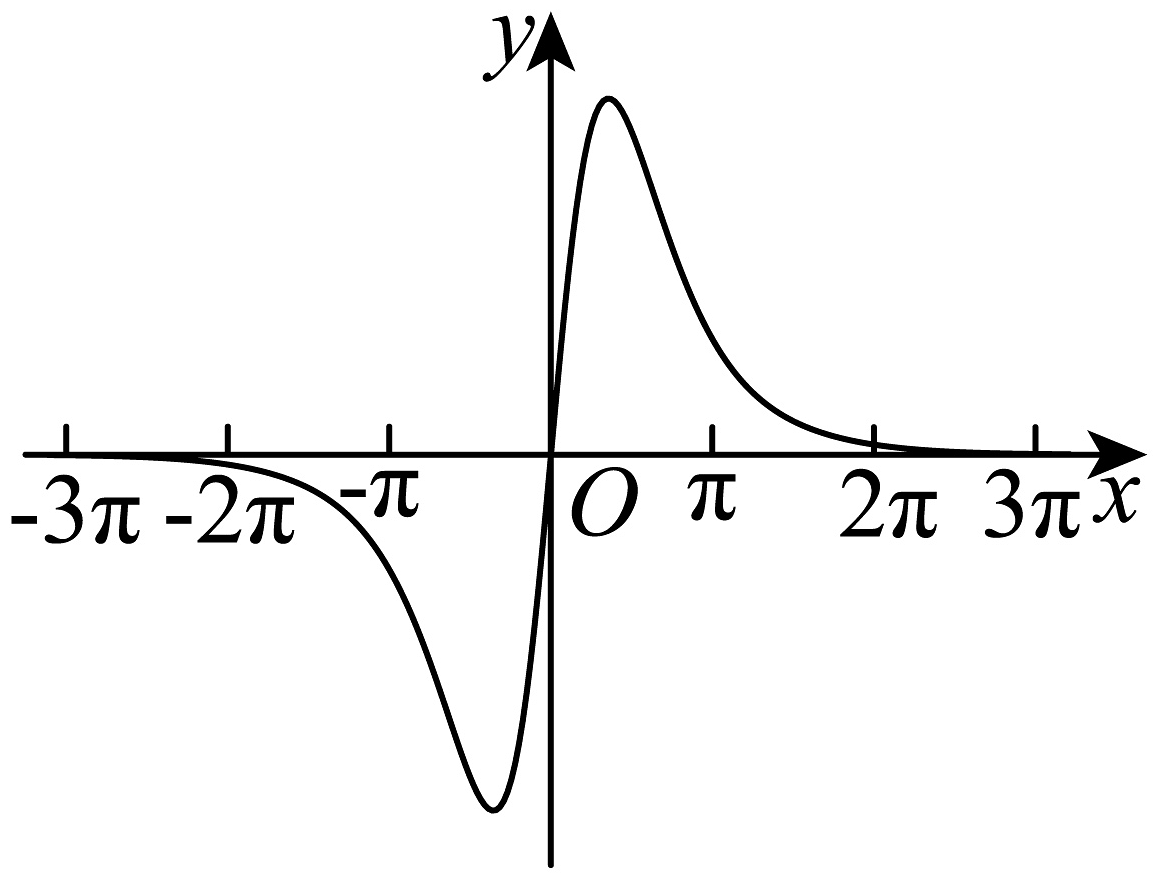
1. 已知全集 , 集合 , , 则( )A、 B、 C、 D、2. 已知命题 , ,则命题 的否定是( )A、 , B、 , C、 , D、 ,3. 函数的图象大致是( )A、
 B、
B、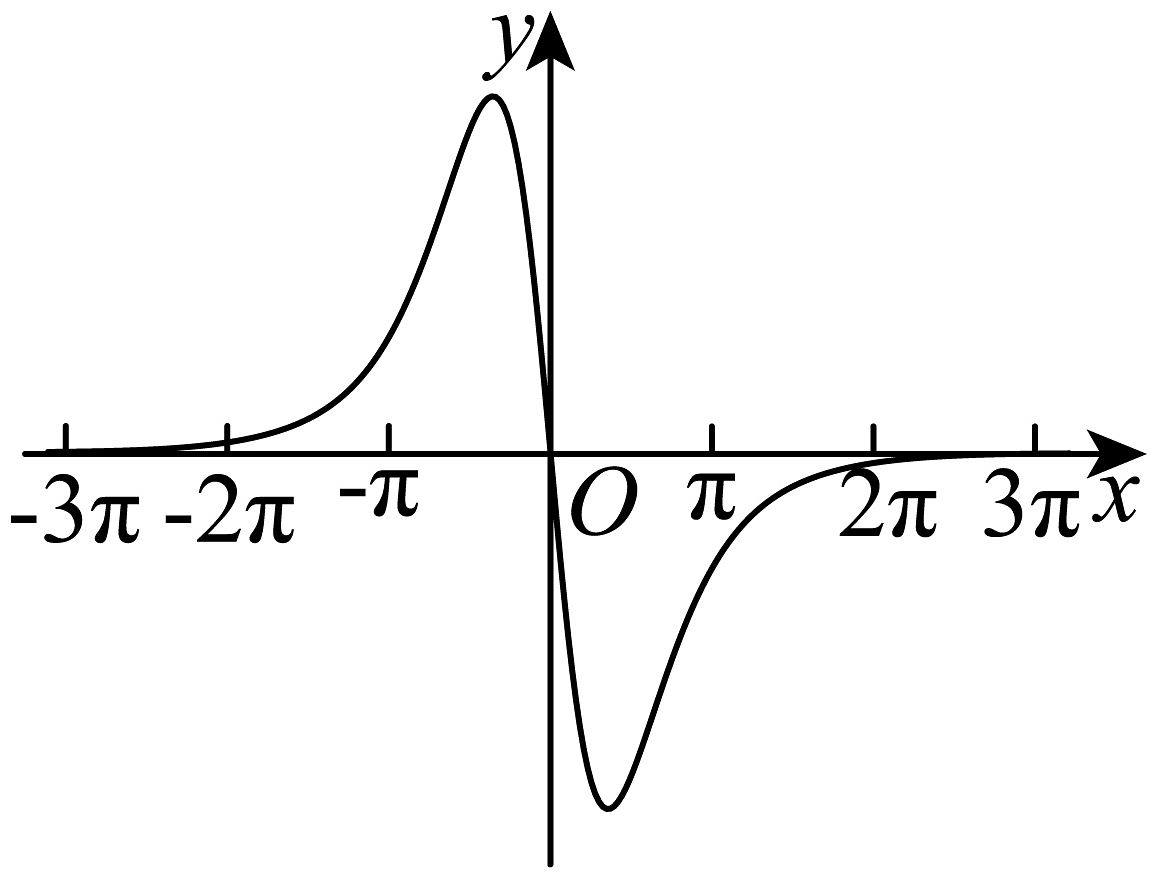 C、
C、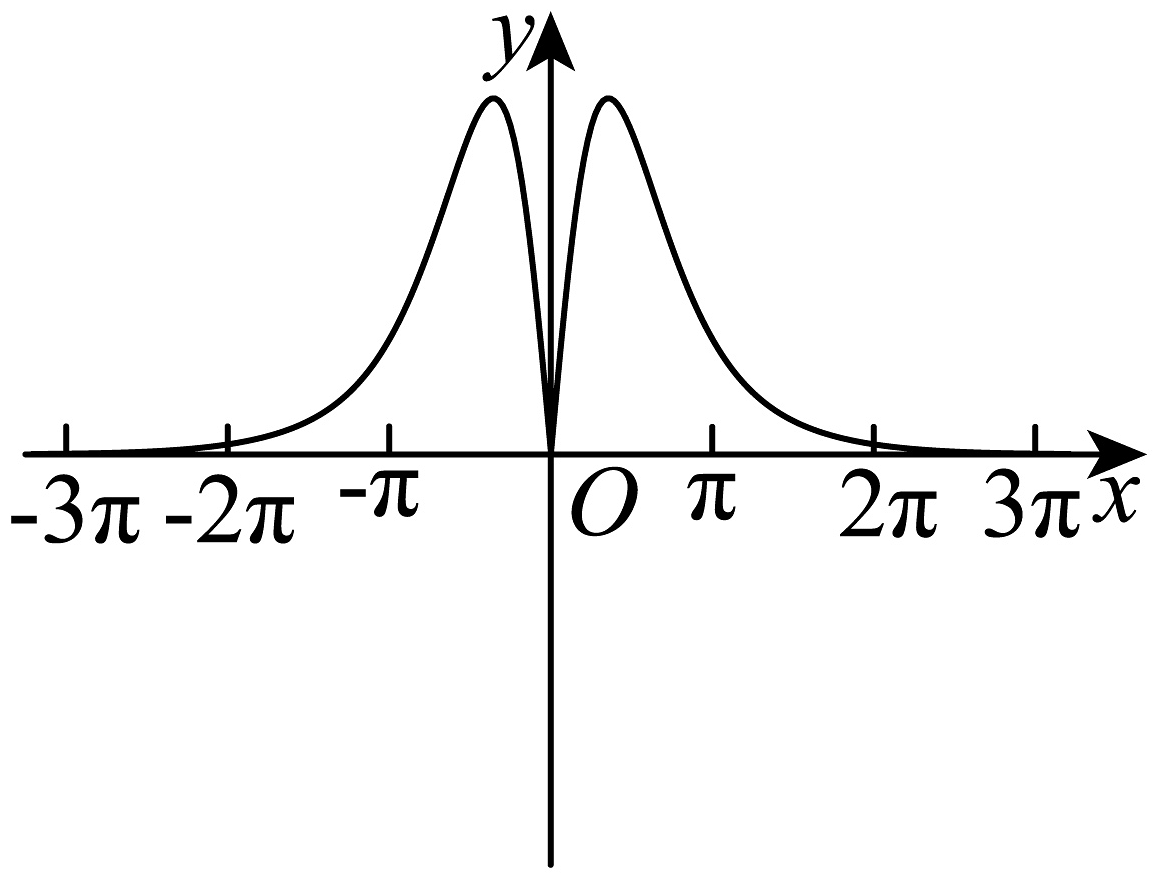 D、
D、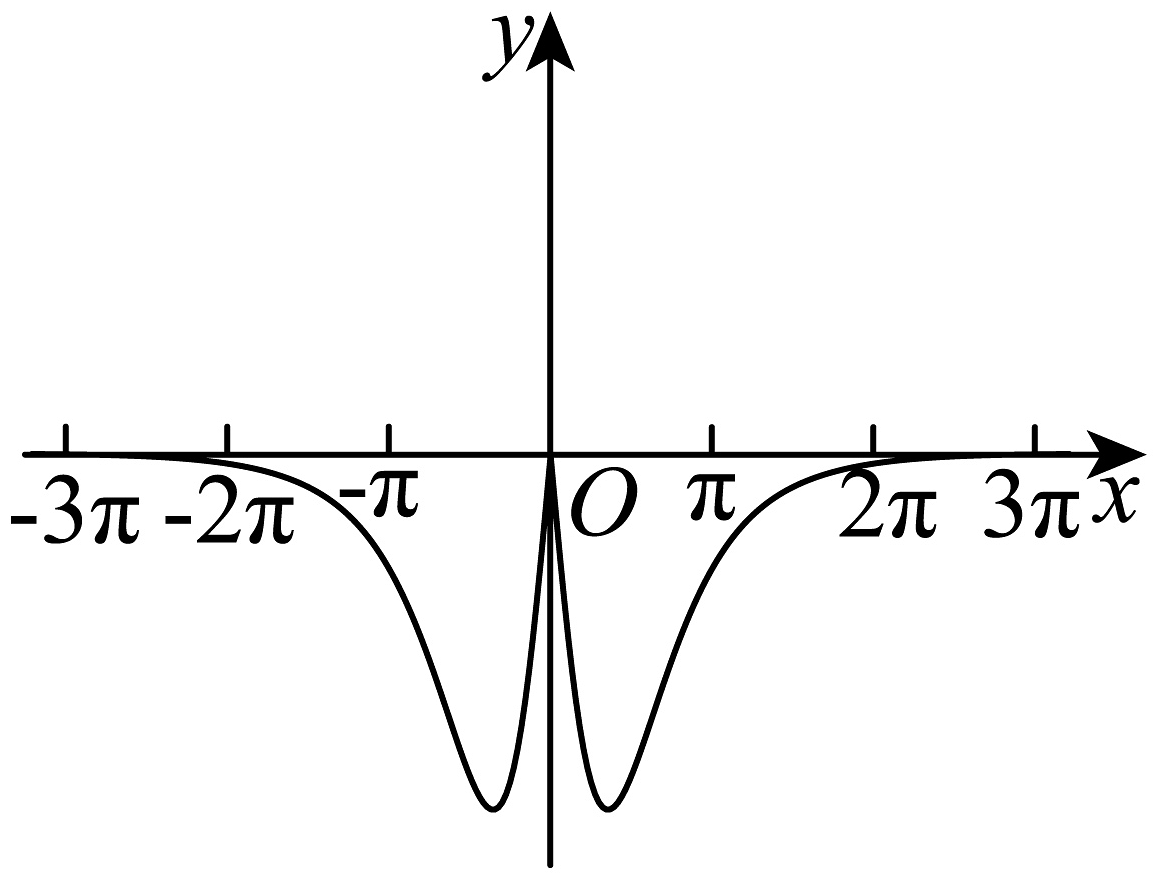 4. 设集合 , , 那么“”是“”的( )A、必要不充分条件 B、充分不必要条件 C、充分必要条件 D、既不充分也不必要条件5. 已知 , , , 则( )A、 B、 C、 D、6. 已知球的表面积为 , 则该球的体积是( )cm3A、64π B、144π C、288π D、216π7. 下列命题错误的是( )A、两个随机变量的线性相关性越强,相关系数的绝对值越接近于 B、设 , 且 , 则 C、线性回归直线一定经过样本点的中心 D、随机变量 , 若 , 则8. 记为等差数列的前项和,且 , 则取最大值时的值为( )A、12 B、12或11 C、11或10 D、109. 函数 , 其中 , 其最小正周期为 , 则下列说法中错误的个数是( )
4. 设集合 , , 那么“”是“”的( )A、必要不充分条件 B、充分不必要条件 C、充分必要条件 D、既不充分也不必要条件5. 已知 , , , 则( )A、 B、 C、 D、6. 已知球的表面积为 , 则该球的体积是( )cm3A、64π B、144π C、288π D、216π7. 下列命题错误的是( )A、两个随机变量的线性相关性越强,相关系数的绝对值越接近于 B、设 , 且 , 则 C、线性回归直线一定经过样本点的中心 D、随机变量 , 若 , 则8. 记为等差数列的前项和,且 , 则取最大值时的值为( )A、12 B、12或11 C、11或10 D、109. 函数 , 其中 , 其最小正周期为 , 则下列说法中错误的个数是( )①
②函数图象关于点对称
③函数图象向右移个单位后,图象关于轴对称,则的最小值为
④若 , 则函数的最大值为
A、1 B、2 C、3 D、4二、填空题(本大题共6小题,共30分)
-
10. 若复数是纯虚数,则实数的值是.11. 已知二项式 , 其展开式中项的系数为.12. 天津是一个历史悠久的文化古都,五大道,石家大院,古文化街,鼓楼这四个景点又是天津十分有名的旅游胜地.已知某游客游览五大道的概率为 , 游览石家大院,古文化街,鼓楼的概率都是 , 且该游客是否游览这四个景点相互独立,则该游客只游览一个景点的概率为;该游客至少游览三个景点的概率为 .13. , , 若2是与的等比中项,则的最小值是.14. 已知中,点是中点,点满足 , 记 , , 请用 , 表示;若 , 向量在向量上的投影向量的模的最小值为 .15. 已知函数若恰有6个不同的实数解,则正实数的取值范围是.
三、解答题(本大题共5小题,共75分.解答应写出文字说明,证明过程或演算步骤)
-
16. 已知函数.(1)、求的单调递增区间;(2)、求在区间上的最大值和最小值.17. 已知的内角 , , , 的对边分别为 , , , 满足(1)、求角的大小;(2)、若 , , 求边的值;(3)、若 , 求的值.
