北师大版数学七年级上册期末检测提升卷（二）

试卷更新日期：2025-12-01 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共24分）

1. 图是正方体的展开图，相对面上的多项式的和相等，则A等于（）

A、 $x^{2} - 4$ B、 $x^{2} - 4 x - 2$ C、 $x^{2} - x - 1$ D、 $x - 1$

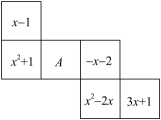查看试题解析
2. 如图，长方形是一个圆柱体的侧面展开图，则这个圆柱体的体积为（）

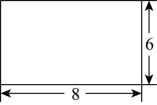A、 $\frac{96}{π}$ B、 $\frac{36}{π}$ 或 $\frac{96}{π}$ C、 $\frac{72}{π}$ D、 $\frac{96}{π}$ 或 $\frac{72}{π}$

查看试题解析
3. 当x=1时，整式( $a x^{3} + b x + 1$ 的值为-2025，则当x=-1时，整式 $a x^{3} + b x - 1$ 的值是( )

A、2025 B、- 2025 C、2024 D、- 2024

查看试题解析
4. 如图，长方形ABCD 的边长AB=DC=x，AD=BC=y。在长方形ABCD内，将一张边长为a和两张边长为b(a>b)的正方形纸片按图1，图2两种方式放置，长方形中未被这三张正方形纸片覆盖的部分用阴影表示，设图2中阴影部分的周长与图1中阴影部分的周长的差为L，若要知道L的值，只要测量图中哪条线段的长( )

A、a B、b C、x D、y

查看试题解析
5. 下列调查方式中，适合采用普查方式的是（）

A、了解一批圆珠笔芯的使用寿命 B、调查市民对“地铁1号线”车站环境的意见 C、调查本市七年级学生的课业负担 D、了解一沓钞票中有没有假钞

查看试题解析
6. 如图，C，D是线段AB 上两点，M，N分别是线段AD，BC的中点，下列结论：①若AD=BM，则AB=3BD；②若AC=BD，则AM=BN；③AC-BD=2(MC-DN)；④2MN=AB-CD.其中所有正确的结论是( )

A、①②③ B、③④ C、①②④ D、①②③④

查看试题解析

二、填空题（每题3分，共15分）

7. 单项式5³a²b的次数是 .

查看试题解析
8. 当x=1时，代数式 $p x^{3} + q x + 1$ 的值为2023，则当x=-1，代数式 $p x^{3} + q x + 1$ 的值为 .

查看试题解析
9. 已知单项式： $2 x^{m + 2} y^{4}$ 与 $5 x^{5} y^{2 + m}$ 是同类项，则 $n^{m} =$ .

查看试题解析
10. 1930年，德国汉堡大学的学生考拉兹，曾经提出过这样一个数学猜想：对于每一个正整数，如果它是奇数，则对它乘3再加1；如果它是偶数，则对它除以2.如此循环，最终都能够得到1.这一猜想后来成为著名的“考拉兹猜想”，又称“奇偶归一猜想”.虽然这个结论在数学上还没有得到证明，但举例验证都是正确的，例如：取正整数5，最少经过下面5步运算可得1，即： $5 \overset{\times 3 + 1}{\to} 16 \overset{+ 2}{\to} 8 \overset{+ 2}{\to} 4 \overset{+ 2}{\to} 2 \overset{+ 2}{\to} 1$ 如果正整数m最少经过6步运算可得到1，则m的值为.

查看试题解析
11. 如图，在∠AOB的内部有3条射线OC，OD，OE．若∠AOC= 51°，∠BOE = $\frac{1}{3}$ ∠BOC，∠BOD= $\frac{1}{3}$ ∠AOB，则∠DOE=°

查看试题解析

三、解答题（共7题，共61分）

12. 已知 $A = 2 a^{2} + 3 a b - 2 a - 1 ， B = a^{2} - \frac{1}{2} a b - \frac{2}{3}$ ．

(1)、当 $a = - 1 ， b = - 2$ 时，求 $A - 2 B$ 的值；

(2)、若 $A - 2 B$ 的值与 $a$ 的取值无关，求 $b$ 的值．

查看试题解析
13. 下面是A，B 两球从不同高度自由下落到地面后反弹高度的统计图。

(1)、比较两个球反弹高度的变化情况，哪个球的弹性大?

(2)、如果两个球下落的起始高度继续增加，那么你认为A球的反弹高度会继续增加吗?B球呢?

(3)、分别比较A球、B球的反弹高度和起始高度，你认为反弹高度会超过起始高度吗?

查看试题解析
14. 记 $M_{(1)} = - 2$ ， $M_{(2)} = (- 2) \times (- 2)$ ， $M_{(3)} = (- 2) \times (- 2) \times (- 2)$ ， …， $M_{(n)} = \underset{n 个 (- 2) 相乘}{\underset{⏟}{(- 2) \times (- 2) \times \dots \times (- 2)}}$ （其中n为正整数）．

(1)、计算： $M_{(5)} + M_{(6)}$ ；

(2)、求 $2 M_{(2024)} + M_{(2025)}$ 的值；

(3)、试说明 $2 M_{(n)}$ 与 $M_{(n + 1)}$ 互为相反数．

查看试题解析
15. 如图，已知线段AB＝4，延长AB到点C，使得AB＝2BC，反向延长AB到点D，使AC＝2AD．

(1)、求线段CD的长；

(2)、若Q为AB的中点，P为线段CD上一点，且BP＝ $\frac{1}{2}$ BC，求线段PQ的长．

查看试题解析
16. 如图， $O M$ 是 $∠ A O C$ 的平分线， $O N$ 是 $∠ B O C$ 的平分线．

(1)、如图1，当 $∠ A O B$ 是直角， $∠ B O C = 60 °$ 时， $∠ M O N$ 的度数是多少？

(2)、如图2，当 $∠ A O B = α$ ， $∠ B O C = 60 °$ 时，猜想 $∠ M O N$ 与α的数量关系；

(3)、如图3，当 $∠ A O B = α$ ， $∠ B O C = β$ 时，猜想： $∠ M O N$ 与α、β有数量关系吗？如果有，指出结论并说明理由．

查看试题解析

17. 牛肉火锅店元旦促销，推出以下两种优惠方式（不能同时使用）：

方案A	在某团上可购买“50代100元代金券”（实付50元就能获得100元的代金券），消费每满100元才能使用1张代金券，最多使用3张．
方案B	除每桌50元的锅底外，其余菜品均打6折．

(1)、若小明一家去该火锅店吃火锅，消费总额原价为220元，并使用方案A买单，实际付款______元；

(2)、若小芳一家去该火锅店吃火锅，并使用方案B方式买单，结账时实际付款308元，请问优惠前消费总额是多少元？

(3)、若小红一家在该火锅店点了一份锅底和其它菜品（消费总额原价超过100元），小红对比两种优惠方式后，发现方案A比方案B贵了30元，请问小红一家消费总额原价是多少？从实惠的角度，实际付款多少钱？

查看试题解析

18. （一）实践准备
李老师带领七一班综合实践小组进行废物再利用的数学制作活动，他们准备用废弃的宣传单制作纸盒（有盖或无盖）．
（二）操作探究
（1）如图是“乐研组”制作的一个正方体纸盒的展开图，正方体的各面分别标有“南，阳，值，得，三，顾”六个字，则“阳”相对面的文字是_________
（2）“爱数组”准备制作一个无盖的正方体纸盒，则下列_________（填字母）图形经过折叠能围成无盖正方体纸盒．
A． B．
C． D．
（三）尝试应用
（3）如图2，这是一张长为 $23cm$ 、宽为 $18cm$ 的长方形包装纸，现要制成牛奶盒子．上下各留宽度均为 $4cm$ 的一个长方形，中间剩余部分用于制作牛奶盒身．如图3，将牛奶盒身分成四块长方形，其中①③长方形大小相同，②④长方形大小也相同，且②号长方形的宽比①号多 $1cm$ ．把图3中的包装纸折成图4中的牛奶盒子，想要装下 ${280cm}^{3}$ 的牛奶是否能成功？为什么？

查看试题解析