一次函数的跨学科应用八年级数学同步测评

试卷更新日期：2025-11-27 类型：同步测试

进入出卷网下载

一、选择题。下列各试题包含不同学科背景，请从数学视角分析问题，并选出正确选项。

1. 某地温度T(℃)与海拔高度h(m)之间的函数关系可用 $T = 10 - \frac{ℎ}{150}$ 来估计，关系式 $T = 10 - \frac{ℎ}{150}$ 中的变量是( )

A、T和10 B、10和 $\frac{ℎ}{150}$ C、10和150 D、T和h

查看试题解析
2. 弹簧挂上物体后会伸长，测得一弹簧的长度 $y (cm)$ 与所挂的物体的质量 $x (kg)$ 之间有下面的关系．

$x / kg$

$0$

$1$

$2$

$3$

$4$

$5$

$y / cm$

$10$

$10.5$

$11$

$11.5$

$12$

$12.5$

下列说法不正确的是（）．

A、 $x$ 与 $y$ 都是变量，且 $x$ 是自变量， $y$ 是因变量 B、弹簧不挂重物时的长度为 C、物体质量每增加，弹簧长度增加 D、所挂物体质量为时，弹簧长度为

查看试题解析
3. 如图，某种杆秤在秤杆的点 $A$ 处固定提纽，点 $B$ 处挂秤盘， $C$ 为 $0$ 刻度点，当秤盘不放物品时，提起提纽，移动秤砣所挂的位置，秤杆处于平衡．若秤盘中放入 $x$ 克物品后，秤砣所挂的位置与提纽的距离为 $y$ 毫米时秤杆处于平衡， $y$ 与 $x$ 的关系式为 $y = 10 + 2 x$ ，当 $x = 25$ 克时， $y$ 的长度是毫米．

查看试题解析
4. 在探究“重力的大小与质量的关系”实验中，下列选项能反映物体重力 $G$ 与质量 $m$ 的函数关系大致图象是( )

A、 B、 C、 D、

查看试题解析
5. 如图表示光线从空气进入水中时的光路图，若按如图所示的方式建立平面直角坐标系，并设入水前与入水后光线所在直线的函数表达式分别为 $y_{1} = k_{1} x, y_{2} = k_{2} x,$ 则关于 k₁与k₂的关系，下列说法正确的是（ )

A、k₁>0，k₂<0 B、 $k_{1} > 0, k_{2} > 0$ C、 $∣ k_{1} ∣ > ∣ k_{2} ∣$ D、 $k_{1} - k_{2} > 0$

查看试题解析
6. 如图所示，l_甲， l_乙分别是甲、乙两弹簧的长y(cm) 与所挂物体质量x(kg)之间函数关系的图象，设甲弹簧每挂1kg物体伸长的长度为k_甲cm，乙弹．簧每挂1kg物体伸长的长度为k_乙cm，则k_甲与k_乙的关系是（）

A、k_甲>k_乙 B、k_甲=k_乙 C、k_甲<k_乙 D、不能确定

查看试题解析
7. 生物学研究表明，某种蛇在一定生长阶段，其体长 $y (c m)$ 是尾长 $x (c m)$ 的一次函数，部分数据如下表所示，则 $y$ 与 $x$ 之间的关系式为（）
尾长 $x (c m)$
6
8
10
体长 $y (c m)$
45.5
60.5
75.5

A、 $y = 7.5 x + 0.5$ B、 $y = 7.5 x - 0.5$ C、 $y = 15 x$ D、 $y = 15 x + 45.5$

查看试题解析
8. 图1是我国青海湖最深处的某一截面图，青海湖水面下任意一点A的压强p（单位：cmHg）与其离水面的深度h（单位：m）的函数解析式为 $P = k h + P_{0}$ ，其图象如图2所示，其中 $P_{0}$ 为青海湖水面大气压强，k为常数且 $k \neq 0$ .根据图中信息分析（结果保留一位小数），下列结论正确的是（）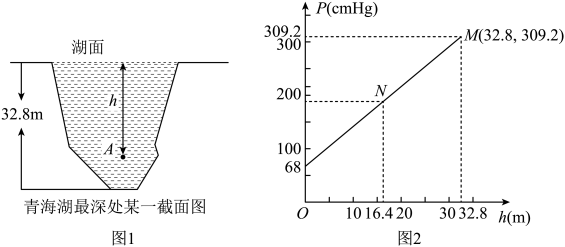

A、青海湖水深16.4m处的压强为188.6cmHg B、青海湖水面大气压强为76.0cmHg C、函数解析式 $P = k h + P_{0}$ 中自变量h的取值范围是 $h \geq 0$ D、P与h的函数解析式为 $P = 9.8 \times 1 0^{5} h + 76$

查看试题解析

二、填空题。请在各学科情境中构建函数模型，并完成填空。

9. 物理课上老师带领学生探究气体压强与气体体积的关系，他们在气缸内充入了一定量的气体，当保证温度不变时，记录气缸内的气体压强 $P (kPa)$ 与气体体积 $V$ （ $m^{3}$ ），数据如下：
气缸内的气体压强 $P (kPa)$
240
200
160
120
96
80
气缸内气体体积 $V$ （m³）
$0.4$
$0.48$
$\begin{array}{l} 0.6 \end{array}$
$0.8$
1
$1.2$
则用式子表示 $P$ 与 $V$ 之间的关系是．

查看试题解析
10. 一个弹簧不挂重物时长 $12 c m$ ，挂上 $1 k g$ 的物体后，弹簧伸长 $2 c m$ ．在弹性限度内，挂上重物后弹簧伸长的长度与所挂重物的质量成正比．则弹簧总长 $y$ （单位： $c m$ ）关于所挂物体质量 $x$ （单位： $k g$ ）的函数解析式为．

查看试题解析
11. 《九章算术》中有一道“凫雁相逢”（凫：野鸭）问题：今有凫起南海七日至北海，雁起北海九日至南海，今凫、雁俱起，问何日相逢？如图是凫、雁起飞后，凫、雁距离南海的路程 $s_{1} ， s_{2}$ 关于飞行时间 $t$ 的函数图象，则两函数图象的交点 $M$ 的横坐标是．

查看试题解析
12. 如图，平面直角坐标系中，一束光经过A（-3，1）照射在平面镜（x轴）上的点B（-1，0）处，其反射光线BC交y轴于点 $C (0, \frac{1}{2}),$ 再被平面镜（y轴）反射得光线CD（其中∠BCO=∠DCE），则直线CD的函数表达式为 .

查看试题解析

三、解答题。请综合运用数学知识与跨学科思维，解决下列实际问题。

13. 某种气体在0℃时的体积为100L，温度每升高1℃，它的体积增加0.37L。

(1)、写出气体体积V(L)与温度t(℃)之间的函数表达式。

(2)、求当温度为30℃时气体的体积。

(3)、当气体的体积为107.4L时，温度为多少摄氏度?

查看试题解析
14. 用充电器给某手机充电时，其屏幕画面显示目前电量为 $20 %$ （如图 1），经测试，在用快速充电器和普通充电器对该手机充电时，其电量 $y$ (单位： %) 与充电时间 $x$ （单位： h）的函数图象分别为图 2 中的线段 $A B, A C$ . 根据以上信息，回答下列问题：

(1)、填空：用普通充电器充电， 3 小时后该手机电量为 $%;$

(2)、先用普通充电器充电 $a h$ 后，再改为快速充电器充满电，一共用时 3 h ，请在图2中画出电量 $y$ (单位：%)与充电时间 $x$ （单位： h）的函数图象，并标注出 $a$ 所对应的值.

查看试题解析

15. 高铁站候车厅的饮水机(图1)有温水、开水两个按钮，图2为其示意.小明先接温水后再接开水，接满

700 m l

的水杯，期间不计热损失.利用图中信息解决下列问题：

物理知识：开水和温水混合时会发生热传递，开水放出的热量等于温水吸收的热量，可转化为：开水体积×开水降低的温度=温水体积×温水升高的温度．
生活经验：饮水最佳温度是35-38℃（包括35℃与38℃），这一温度最接近人体体温．

(1)、若先接温水26秒，求再接开水的时间.

(2)、设接温水的时间为

x

秒，接到水杯中水的温度为

y^{°} C

①若 $y = 50$ ，求 $x$ 的值.

②求 $y$ 关于 $x$ 的函数关系式，并写出达到最佳水温时 $x$ 的取值范围.

查看试题解析

$x / kg$	$0$	$1$	$2$	$3$	$4$	$5$
$y / cm$	$10$	$10.5$	$11$	$11.5$	$12$	$12.5$

气缸内的气体压强 $P (kPa)$	240	200	160	120	96	80
气缸内气体体积 $V$ （m³）	$0.4$	$0.48$	$\begin{array}{l} 0.6 \end{array}$	$0.8$	1	$1.2$

尾长 $x (c m)$	6	8	10
体长 $y (c m)$	45.5	60.5	75.5

一次函数的跨学科应用 八年级数学同步测评

一、选择题。下列各试题包含不同学科背景，请从数学视角分析问题，并选出正确选项。

二、填空题。请在各学科情境中构建函数模型，并完成填空。

三、解答题。请综合运用数学知识与跨学科思维，解决下列实际问题。

一次函数的跨学科应用八年级数学同步测评