6.1《平均数与方差》（2）—北师大版数学八年级上册课堂分层训练

试卷更新日期：2025-11-23 类型：同步测试

进入出卷网下载

一、基础夯实

1. 如果样本方差 $s^{2} = \frac{1}{25} [{(x_{1} - 19)}^{2} + {(x_{2} - 19)}^{2} + \dots + {(x_{25} - 19)}^{2}]$ ，那么这个样本的平均数和样本容量分别是（）

A、25，25 B、25，19 C、19，19 D、19，25

查看试题解析
2. 某篮球队5名场上队员的身高（单位：cm）分别是：190，194，198，200，202，现用一名身高为 $196 cm$ 的队员换下场上身高为 $190 cm$ 的队员．与换人前相比，下列对5名场上队员身高的平均数和方差描述正确的是（）

A、平均数变小，方差变小 B、平均数变小，方差变大 C、平均数变大，方差变小 D、平均数变大，方差变大

查看试题解析
3. 科技是第一生产力，创新是第一动力，教育、科技、人才是全面建设社会主义现代化国家的基础性、战略性支撑．某校准备从甲、乙、丙、丁四个科技小组中选出一组，参加坪山区中小学科技创新竞赛，下表记录了各组平时成绩的平均数（单位：分）及方差．若要选出一个成绩好且状态稳定的小组去参加比赛，则应选择的小组是（）
甲
乙
丙
丁
平均数
93
97
97
95
方差
0.8
0.8
1.2
1.2

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 在一次投篮训练中，甲、乙、丙、丁四人各进行10次投篮，每人投篮成绩的平均数都是8，方差分别为 $s_{甲}^{2} = 0.24$ ， $s_{乙}^{2} = 0.42$ ， $s_{丙}^{2} = 0.56$ ， $s_{丁}^{2} = 0.75$ ，成绩最稳定的是（）

A、甲． B、乙 C、丙 D、丁

查看试题解析
5. 为提高学生的运算能力，某校开展“计算小达人”活动，已知甲班10名学生测试成绩的方差 $s_{甲}^{2} = 1.27$ ，乙班10名学生测试成绩的方差 $s_{乙}^{2} = 0.5$ ，两班学生测试成绩的平均分都是95分，则（填“甲班”或“乙班”）的成绩更稳定．

查看试题解析
6. 某村欲购进一批杏树，考察中随机从甲、乙、丙、丁四个品种中各选了 $10$ 棵，每棵产量（单位： $kg$ ）的平均数 $\bar{x}$ 及方差 $s^{2}$ 如表所示：
统计量
甲
乙
丙
丁
$\bar{x}$
$40$
$40$
$38$
$38$
$s^{2}$
$1.8$
$2.3$
$1.8$
$2.3$
该村准备从这四个品种中选出一种产量既高又稳定的杏树，则应选的品种是．

查看试题解析

7. 甲、乙两人在

5

次打靶测试中命中的环数如下：

	第一次	第二次	第三次	第四次	第五次
甲	$8$	$8$	$7$	$8$	$9$
乙	$6$	$9$	$7$	$9$	$9$

从数据来看，谁的成绩较稳定？请你通过计算方差说明理由.

查看试题解析

8. 南明区某学校七、八年级举行“一二 $\cdot$ 九”演讲比赛，根据初赛成绩各选出了 $5$ 名选手 $($ 编号分别为 $1$ 、 $2$ 、 $3$ 、 $4$ 、 $5)$ 组成七年级代表队、八年级代表队参加学校决赛，根据这 $10$ 名选手的决赛成绩 $($ 满分为 $100$ 分 $)$ ，制作了如下的统计图表：
二
平均数
中位数
众数
方差
七年级
$85$
$85$
$m$
$70$
八年级

$80$
$100$

(1)、表格中 $m =$ ；

(2)、请求出八年级代表队参加学校决赛的平均成绩；

(3)、要从这两个年级代表队中选出一个年级，代表学校去参加南明区的比赛，你认为应该选择哪个年级代表队？请说明理由．

查看试题解析

二、能力提升

9. 某学校计划组织“垫排球”比赛活动，为了解参赛学生垫排球水平及稳定程度，在比赛前期分别记录了甲、乙、丙、丁四名参赛学生在规定时间内10次垫排球的数量，并计算出了各自的平均个数 $\bar{x}$ 及方差 $S^{2}$ ，如表所示：
参赛学生
甲
乙
丙
丁
$\bar{x}$
51
53
55
55
$S^{2}$
$\frac{23}{4}$
$\frac{21}{4}$
6
$\frac{21}{4}$
根据上表所列数据，你认为参赛学生中获胜的可能性最大的是（　　）

A、甲 B、乙 C、丙 D、丁

查看试题解析

10. 一城市准备选购一千株高度大约为2m的某种风景树来进行街道绿化，有四个苗圃生产基地投标（单株树的价格都一样）．采购小组从四个苗圃中都任意抽查了20株树苗的高度，得到的数据如下：

	树苗平均高度（单位：m）	标准差
甲苗圃	1.8	0.2
乙苗圃	1.8	0.6
丙苗圃	2.0	0.6
丁苗圃	2.0	0.2

请你帮采购小组出谋划策，应选购（）

A、甲苗圃的树苗 B、乙苗圃的树苗； C、丙苗圃的树苗 D、丁苗圃的树苗

查看试题解析

11. 某滑雪俱乐部12名会员被分成甲、乙两组，他们的身高情况如图所示，甲组身高的平均数为 $\bar{x_{甲}} = 176 c m$ ，则下列结论正确的是（）

A、 $\bar{x_{甲}} = \bar{x_{乙}}$ ， $s_{甲}^{2} < s_{乙}^{2}$ B、 $\bar{x_{甲}} = \bar{x_{乙}}$ ， $s_{甲}^{2} > s_{乙}^{2}$ C、 $\bar{x_{甲}} < \bar{x_{乙}}$ ， $s_{甲}^{2} < s_{乙}^{2}$ D、 $\bar{x_{甲}} > \bar{x_{乙}}$ ， $s_{甲}^{2} > s_{乙}^{2}$

查看试题解析
12. 已知样本 $x_{1}$ 、 $x_{2}$ ， $⋯$ ， $x_{n}$ 平均数是 $5$ ，方差是 $3$ ，则样本 $3 x_{1} + 5$ ， $3 x_{2} + 5$ ， …， $3 x_{n} + 5$ 的平均数和方差是（）

A、 $5 ， 3$ B、 $20 ， 3$ C、 $20 ， 27$ D、 $5 ， 27$

查看试题解析
13. 已知一组数据的方差s²= $\frac{1}{4}$ [（x₁﹣6）²+（x₂﹣6）²+（x₃﹣6）²+（x₄﹣6）²]，那么这组数据的总和为．

查看试题解析
14. 在方差计算公式 $s^{2} = \frac{1}{20} [{(x_{1} - 15)}^{2} + {(x_{2} - 15)}^{2} + ⋯ + {(x_{20} - 15)}^{2}]$ 中，可以看出 $x_{1} + x_{2} + \dots x_{20}$ 的值为．

查看试题解析
15. 为庆况神舟十五号发射成功，学校开展航天知识竞赛活动.经过几轮筛选，本班决定从甲、乙、丙、丁四名同学中选择一名同学代表班级参加比赛，经过统计，四名同学成绩的平均数（单位：分）及方差（单位：分 $^{2}$ ）如表所示：

甲
乙
丙
丁
平均数
98
96
98
95
方差
0.4
2
1.6
0.4
若要选一名成绩好且状态稳定的同学参赛，那么应该选择.

查看试题解析
16. 八年级二班举办了主题为“致敬航天人，共筑星河梦”的演讲比赛．由学生1，学生2，老师、班长一起组成四人评委团，对演讲者现场打分，满分10分．图1是甲、乙二人的演讲得分的不完整折线图，已知二人得分的平均数都是8分．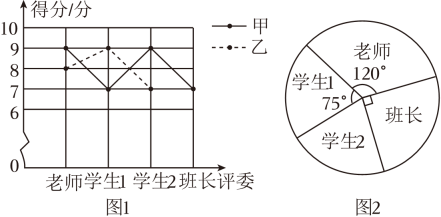

(1)、班长给乙的打分是 ▲ 分，补全折线图；

(2)、在参加演讲的同学中，如果某同学得分的四个数据的方差越小，则认为评委对该同学演讲的评价越一致．请通过计算推断评委对甲、乙两位同学中哪位同学的评价更一致；

(3)、要在甲、乙两位同学中选出一人参加年级的演讲比赛．按照扇形统计图（图2）中各评委的评分占比，分别计算两人各自的最后得分，得分高的能被选中，请判断谁被选中．

查看试题解析

17. 为选派一名学生参加全市实践活动技能竞赛，A，B两位同学在校实习基地现场进行加工直径为20mm的零件的测试，他俩加工的10个零件的相关数据依次如下图表所示（单位：mm）．

根据测试得到的有关数据，试解答下列问题：

	平均数	方差	完全符合要求的个数
A	20	0.026	2
B	20	S²B	5

(1)、考虑平均数与完全符合要求的个数，你认为的成绩好些．

(2)、计算出SB²的大小，考虑平均数与方差，说明谁的成绩好些．

(3)、考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况，你认为派谁去参赛较合适？说明你的理由．

查看试题解析

统计量	甲	乙	丙	丁
$\bar{x}$	$40$	$40$	$38$	$38$
$s^{2}$	$1.8$	$2.3$	$1.8$	$2.3$

二	平均数	中位数	众数	方差
七年级	$85$	$85$	$m$	$70$
八年级		$80$	$100$

参赛学生	甲	乙	丙	丁
$\bar{x}$	51	53	55	55
$S^{2}$	$\frac{23}{4}$	$\frac{21}{4}$	6	$\frac{21}{4}$

6.1《 平均数与方差》（2）—北师大版数学八年级上册课堂分层训练

一、基础夯实

二、能力提升

6.1《平均数与方差》（2）—北师大版数学八年级上册课堂分层训练