北师大版数学八年级上册单元分层检测卷第五章 《二元一次方程组》B卷
试卷更新日期:2025-11-23 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 《九章算术》中有一段文字的大意是:有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还差3钱.问合伙人数、羊价各是多少?设合伙人数为人,羊价为钱,则可列方程组为( )A、 B、 C、 D、2. 点在直线上,坐标是二元一次方程的解,则点P的位置在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 小红学习了等式的性质后,在甲、乙两台天平的左右两边分别放入“■”“●”“▲”三种物体,如图所示,天平都保持平衡.若设“■”与“●”的质量分别为 , , 则下列关系式正确的是 ( )
 A、 B、 C、 D、4. 二元一次方程组 的解是( )A、 B、 C、 D、5. 已知关于的二元一次方程组的解满足 , 则m的值为( )A、0 B、1 C、2 D、36. 下列4组数中,不是二元一次方程的解是( )A、 B、 C、 D、7. 关于x,y的方程组的解满足 , 则的值是( )A、1 B、2 C、4 D、88. 【素材1】某景区游览路线及方向如图所示,①④⑥各路段路程相等,⑤⑦⑧各路段路程相等,②③两路段路程相等.
A、 B、 C、 D、4. 二元一次方程组 的解是( )A、 B、 C、 D、5. 已知关于的二元一次方程组的解满足 , 则m的值为( )A、0 B、1 C、2 D、36. 下列4组数中,不是二元一次方程的解是( )A、 B、 C、 D、7. 关于x,y的方程组的解满足 , 则的值是( )A、1 B、2 C、4 D、88. 【素材1】某景区游览路线及方向如图所示,①④⑥各路段路程相等,⑤⑦⑧各路段路程相等,②③两路段路程相等.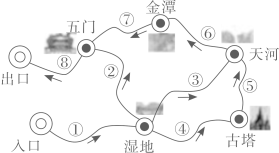
【素材2】设游玩行走速度恒定,经过每个景点都停留20分钟.小温游路线①④⑤⑥⑦⑧用时3小时25分钟;小州游路线①②⑧,他离入口的路程与时间的关系(部分数据)如图所示,在2100米处,他到出口还要走10分钟.

【问题】路线①③⑥⑦⑧各路段路程之和为( )
A、4200米 B、4800米 C、5200米 D、5400米9. 某班环保小组收集废旧电池,数据统计如下表.问1节5号电池和1节7号电池的质量分别是多少?设1节5号电池的质量为x克,1节7号电池的质量为y克,列方程组,由消元法可得x的值为( )5号电池(节)
7号电池(节)
总质量(克)
第一天
2
2
72
第二天
3
2
96
A、12 B、16 C、24 D、2610. 在同一平面直角坐标系中,一次函数与的图象如图所示,小星根据图象得到如下结论: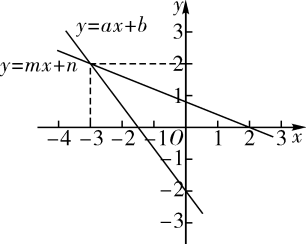
①在一次函数的图象中,的值随着值的增大而增大;②方程组的解为;③方程的解为;④当时,.
其中结论正确的个数是( )
A、1 B、2 C、3 D、4二、填空题(每题3分,共18分)
-
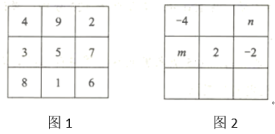
11. 若关于x、y的二元一次方程组的解是 , 则关于x、y的方程组的解是 .12. 我国古代数学名著《张丘建算经》中有这样一题:一只公鸡值5钱,一只母鸡值3钱,3只小鸡值1钱,现花100钱买了100只鸡.若公鸡有8只,设母鸡有x只,小鸡有y只,可列方程组为。13. 点Q的横坐标为一元一次方程的解,纵坐标为的值,其中a,b满足二元一次方程组 , 则点Q关于y轴对称点的坐标为 .14. 幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”.把洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图1),将9个数填在3×3(三行三列)的方格中,如果满足每个横行、每个竖列、每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方.图2的方格中填写了一些数字和字母,若能构成一个广义的三阶幻方,则mn= .
 15. 若实数m,n满足 ,则 .16. 如图,在同一平面直角坐标系中,直线l1:y x 与直线l2:y=kx+3相交于点A,则方程组 的解为 .
15. 若实数m,n满足 ,则 .16. 如图,在同一平面直角坐标系中,直线l1:y x 与直线l2:y=kx+3相交于点A,则方程组 的解为 .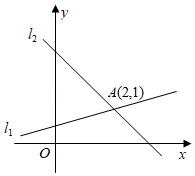
三、解答题(共8题,共72分
-
17. 解下列方程组:(1)、;(2)、 .18. 解下列方程组:(1)、(2)、19. 请你根据下列素材,完成有关任务.
背景
某校计划购买篮球和排球,供更多学生参加体育锻炼,增强身体素质.
素材一
购买2个篮球与购买3个排球需要的费用相等;
素材二
购买2个篮球和5个排球共需800元;
素材三
该校计划购买篮球和排球共60个,篮球和排球均需购买,且购买排球的个数不超过购买篮球个数的2倍.
请完成下列任务:
任务一
每个篮球,每个排球的价格分别是多少元?
任务二
给出最节省费用的购买方案.
20. 国家卫健委在全民健康调查中发现,近年来的肥胖人群快速增长,为加强对健康饮食的重视,特发布各地区四季健康饮食食谱.现有A、B两种食品,每份食品的质量为50g , 其核心营养素如下:食品类别
能量(单位:Kcal)
蛋白质(单位:g)
脂肪(单位:g)
碳水化合物(单位:g)
A
240
12
7.5
29.8
B
280
13
9
27.6
(1)、若要从这两种食品中摄入1280Kcal能量和62g蛋白质,应运用A、B两种食品各多少份?(2)、若每份午餐选用这两种食品共300g,从A、B两种食品中摄入的蛋白质总量不低于76g , 且能量最低,应选用A、B两种食品各多少份?21. 某校积极开展劳动教育,两次购买A , B两种型号的劳动用品,购买记录如下表:A型劳动用品(件)
B型劳动用品(件)
合计金额(元)
第一次
20
25
1150
第二次
10
20
800
(1)、求A , B两种型号劳动用品的单价;(2)、若该校计划再次购买A , B两种型号的劳动用品共40件,其中A型劳动用品购买数量不少于10件且不多于25件.该校购买这40件劳动用品至少需要多少元?(备注:A , B两种型号劳动用品的单价保持不变)22. 某超市从某水果种植基地购进甲、乙两种优质水果,经调查,这两种水果的进价和售价如表所示:水果种类
进价(元/千克)
售价(元/千克)
甲
a
22
乙
b
25
该超市购进甲种水果18千克和乙种水果6千克需366元:购进甲种水果30千克和乙种水果15千克需705元.
(1)、求a , b的值;(2)、该超市决定每天购进甲、乙两种水果共150千克进行销售,其中甲种水果的数量不少于50千克,且不大于120千克.实际销售时,若甲种水果超过80千克,则超过部分按每千克降价5元销售.求超市当天销售完这两种水果获得的利润y(元)与购进甲种水果的数量x(千克)之间的函数关系式(写出自变量x的取值范围),并求出在获得最大利润时,超市的进货方案以及最大利润.23. 如图,在平面直角坐标系xOy中,已知正比例函数 与一次函数 的图象交于点A. (1)、求点A的坐标;(2)、设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交 和 的图象于点B、C,连接OC.若BC= OA,求△OBC的面积.24. 综合与探究
(1)、求点A的坐标;(2)、设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交 和 的图象于点B、C,连接OC.若BC= OA,求△OBC的面积.24. 综合与探究【课本再现】
七年级下册教材页中我们曾探究过“以方程的解为坐标的点的特性”,了解了二元一次方程的解与其图象上点的坐标的关系.我们知道,二元一次方程有无数个解,在平面坐标系中,我们标出以这个方程的解为坐标(的值为横坐标、的值为纵坐标)的点,就会发现这些点在同一条直线上.例如: , 是方程的解,对应点、 . 如图所示,我们在平面坐标系中将其标出,另外,方程的解还对应点、……将这些点连起来正好是一条直线,反过来,在这条直线上任取一点,这个点的坐标也对应方程的解,所以我们把这条直线就叫做方程的图象.
结论:一般的,以一个二元一次方程的解为坐标的点的全体叫做这个方程的图象,任意一个二元一次方程的图象都是一条直线.
 (1)、解决问题】
(1)、解决问题】已知、、 , 则点(填“或或”)在方程的图象上.
(2)、已知无论为何值,关于、的二元一次方程的图象都经过某一定点,且这个定点在方程的图象上,求的值.(3)、【拓展延伸】已知为实数,为正整数,关于、的方程组的解也为正整数,且以此方程组的解为坐标的点在方程的图象上,求的值.