北师大版数学八年级上册单元分层检测卷第四章《一次函数》B卷

试卷更新日期：2025-11-16 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 已知一次函数 $y = k x + b (k \neq 0)$ 的图像经过点 $M (1 ， 2)$ ，且 y 随 x 的增大而增大. 若点 N 在该函数的图象上，则点 N 的坐标可以是（）

A、(-2，2) B、(2，1) C、(-1，3) D、(3，4)

查看试题解析
2. 对于一次函数 $y = 2 x - 1$ ，下列结论正确的是（）

A、它的图象与 $y$ 轴交于点 $(0, - 1)$ B、 $y$ 随 $x$ 的增大而减小 C、当 $x > \frac{1}{2}$ 时， $y < 0$ D、它的图象经过第一、二、三象限

查看试题解析
3. 已知一次函数 $y = k x + b$ 的图象如图所示，则 $k$ ， $b$ 的取值范围是（）

A、 $k > 0$ ， $b < 0$ B、 $k < 0$ ， $b < 0$ C、 $k < 0$ ， $b > 0$ D、 $k > 0$ ， $b > 0$

查看试题解析
4. 一次函数y＝kx﹣1（k≠0）的函数值y随x的增大而减小，它的图象不经过的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 如图，甲、乙两车从A地出发前往B地，在整个行程中，汽车离开A地的路程y(km)与时刻t之间的对应关系如图所示，下列结论错误的是( )

A、乙车先到达B地 B、A、B两地相距300km C、甲车的平均速度为 100km/h D、在8：30时，乙车追上甲车

查看试题解析
6. 如图，在同一平面直角坐标系中，一次函数 $y = k_{1} x + b_{1}$ 与 $y = k_{2} x + b_{2}$ （其中 $k_{1} k_{2} \neq 0$ ， $k_{1}$ ， $k_{2}$ ， $b_{1}$ ， $b_{2}$ 为常数）的图象分别为直线 $l_{1}$ ， $l_{2}$ .下列结论正确的是（）

A、 $b_{1} + b_{2} > 0$ B、 $b_{1} b_{2} > 0$ C、 $k_{1} + k_{2} < 0$ D、 $k_{1} k_{2} < 0$

查看试题解析
7. 一辆快车从A地匀速驶向B地，一辆慢车从B地匀速驶向A地，两车同时出发，各自到达目的地后停止．两车之间的距离s（km）与行驶时间t（h）之间的函数关系如图所示，下列结论错误的是（　　）

A、两车出发2h后相遇 B、A ， B两地相距280km C、快车比慢车早 $\frac{3}{2}$ h到达目的地 D、快车的速度为80km/h ，慢车的速度为60km/h

查看试题解析
8. 如图1“燕几”即宴几，是世界上最早的一套组合桌，由北宋进士黄伯思设计.全套“燕几”一共有七张桌子，包括两张长桌、两张中桌和三张小桌，每张桌面的宽都相等.七张桌面分开可组合成不同的图形.如图2给出了《燕几图》中名称为“回文”的桌面拼合方式，若设每张桌面的宽为 $x$ 尺，长桌的长为 $y$ 尺，则 $y$ 与 $x$ 的关系可以表示为（）

A、 $y = 3 x$ B、 $y = 4 x$ C、 $y = 3 x + 1$ D、 $y = 4 x + 1$

查看试题解析
9. 在平面直角坐标系中．将函数 $y = x$ 的图象绕坐标原点逆时针旋转 $90 °$ ，再向上平移1个单位长度，所得直线的函数表达式为（）

A、 $y = - x + 1$ B、 $y = x + 1$ C、 $y = - x - 1$ D、 $y = x - 1$

查看试题解析
10. 甲、乙两人沿相同路线由A地到B地匀速前进，两地之间的路程为20km ．两人前进路程s（单位：km）与甲的前进时间t（单位：h）之间的对应关系如图所示．根据图象信息，下列说法正确的是（）

A、甲比乙晚出发1h B、乙全程共用2h C、乙比甲早到B地3h D、甲的速度是5km/h

查看试题解析

二、填空题（每题3分，共18分）

11. 甲、乙两人在一次100米赛跑比赛中，路程s（米）与时间t（秒）的函数关系如图所示，填（“甲”或“乙”先到终点）．

查看试题解析
12. 如图，一次函数y＝kx+b的图象经过A（3，6）、B（0，3）两点，交x轴于点C ，则△AOC的面积为．

查看试题解析
13. 学校提倡“低碳环保，绿色出行”，小明和小亮分别选择步行和骑自行车上学，两人各自从家同时同向出发，沿同一条路匀速前进．如图所示， $l_{1}$ 和 $l_{2}$ 分别表示两人到小亮家的距离 $s (k m)$ 和时间 $t (h)$ 的关系，则出发h后两人相遇．

查看试题解析
14. 如图，在平面直角坐标系中，直线AB交x轴于点A（1，0），交y轴于点B（0，2），以原点O为圆心，适当长为半径画弧，交x轴于点C ，交y轴于点D ，分别以点C ， D为圆心，大于 $\frac{1}{2}$ CD的长为半径画弧，两弧在第一象限内交于点E ，作射线OE交AB于点F ，则点F的坐标是．

查看试题解析
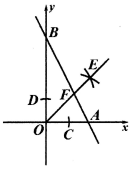15. 已知直线y=m（x+1）（m≠0）与直线y=n（x-2）（n≠0）的交点在y轴上，则 $\frac{n}{m} + \frac{m}{n}$ 的值是.

查看试题解析
16. 一辆汽车在行驶过程中，其行驶路程 $y$ （千米）与行驶时间 $x$ （小时）之间的函数关系如图所示．当 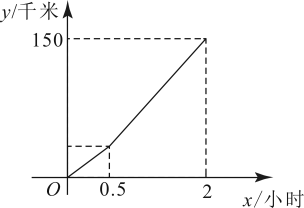$0 \leq x \leq 0.5$ 时， $y$ 与 $x$ 之间的函数表达式为 $y = 60 x$ ；当 $0.5 \leq x \leq 2$ 时， $y$ 与 $x$ 之间的函数表达式为．

查看试题解析

三、解答题（共8题，共72分）

17. 研究表明，一定质量的气体，在压强不变的条件下，气体体积 $y (L)$ 与气体温度 $x (℃)$ 成一次函数关系．某实验室在压强不变的条件下，对一定质量的某种气体进行加热，测得的部分数据如下表：
气体温度 $x (℃)$
…
25
30
35
…
气体体积 $y (L)$
…
596
606
616
…

(1)、求 $y$ 与 $x$ 的函数关系式；

(2)、为满足下一步的实验需求，本次实验要求气体体积达到 $700 L$ 时停止加热．求停止加热时的气体温度．

查看试题解析
18. 某品牌储水机的容量是200升，当加水加满时，储水机会自动停止加水，已知加冷水量y（升）和时间x（分钟）的图象如图所示，加水过程中，水的温度t（摄氏度）和x（分钟）的关系： $t = \frac{20 x + 100}{x + 2}$

(1)、求y与x的函数关系式，并写出定义域；

(2)、求储水机中的水加满时，储水机内水的温度．

查看试题解析
19. 某药品研究所开发一种抗菌新药．经多年动物实验，首次用于临床人体试验．测得成人服药后血液中药物浓度y（微克/毫升）与服药后时间x（时）之间满足一次函数关系（如图）．服药后3小时，测得血液中药物浓度达到最高值9微克/毫升；服药后11小时，测得血液中药物浓度为1微克/毫升．

(1)、请分别求出血液中药物浓度上升阶段和下降阶段y与x之间的函数关系式；

(2)、根据测试，成人服药后，血液中药物浓度不低于3微克/毫升时，才能对人体产生抗菌作用，试求成人服药后，药物对人体产生抗菌作用的有效时长．

查看试题解析
20. 甲、乙两人从同一地点 $M$ 出发沿同一路线匀速步行前往 $N$ 处参加活动．甲比乙早出发 $6 m i n$ ，两人途中均未休息，先到达 $N$ 处的人在原地休息等待，直到另一人到达 $N$ 处．两人之间的路程 $y (m)$ 与甲行走的时间 $t (m i n)$ 的函数图象如图所示．

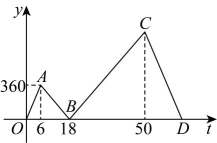(1)、乙步行的速度为 $m / m i n, M N$ 之间的路程为 $m$ ；

(2)、当 $18 \leq t \leq 50$ 时，求 $y$ 关于 $t$ 的函数表达式；

(3)、甲出发多长时间时，两人之间的路程为 $450 m$ ．

查看试题解析
21. 山东省在能源绿色低碳转型过程中，探索出一条“以储调绿”的能源转型路径．某地结合实际情况，建立了一座圆柱形蓄水池，通过蓄水发电实现低峰蓄能、高峰释能，助力能源转型．
已知本次注水前蓄水池的水位高度为 $5$ 米，注水时水位高度每小时上升 $6$ 米．

(1)、请写出本次注水过程中，蓄水池的水位高度 $y ($ 米 $)$ 与注水时间 $x ($ 小时 $)$ 之间的关系式；

(2)、已知蓄水池的底面积为 $0.4$ 万平方米，每立方米的水可供发电 $0.3$ 千瓦时，求注水多长时间可供发电 $4.2$ 万千瓦时？

查看试题解析
22. 自主研发和创新让我国的科技快速发展，“中国制造”正引领世界湖流、某科技公司计划投入一笔资金用来购买A、B两种型号的芯片.已知购买1颗A型芯片和2颗B型芯片共需要750元，购买2颗A型芯片和3颗B型芯片共要1300元.

(1)、求购买1颗A型芯片和1颗B型芯片各需要多少元.

(2)、若该公司计划购买A、B两种型号的芯片共8000题，其中购买A型芯片的数量不少于B型芯片数量的3倍.当购买A型芯片多少颗时、所需资金最少，最少资金是多少元.

(3)、该公司用甲、乙两辆芯片运输车，先后从M地出发，沿着同一条公路匀速行驶，前往目的地N，两车到达N地后均停止行驶.如图，yp（km）、yz（km）分别是甲、乙两车离M地的距离与甲车行驶的时间x（h）之间的函数关系，请根据图象信息解答下列问题：
①甲车的速度是km/h.
②当甲、乙两车相距30km时，直接写出x的值.

查看试题解析
23. 一条公路上依次有A、B、C三地，一辆轿车从A地出发途经B地接人，停留一段时间后原速驶往C地；一辆货车从C地出发，送货到达B地后立即原路原速返回C地（卸货时间忽略不计）。两车同时出发，轿车比货车晚 $\frac{1}{3} h$ 到达终点，两车均按各自速度匀速行驶。如图是轿车和货车距各自出发地的距离y（单位：km）与轿车的行驶时间x（单位：h）之间的函数图象，结合图象回答下列问题：

(1)、图中a的值是， b的值是；

(2)、在货车从B地返回C地的过程中，求货车距出发地的距离y（单位：km）与行驶时间x（单位：h）之间的函数解析式；

(3)、直接写出轿车出发多长时间与货车相距40km。

查看试题解析
24. 【知识链接】
实验目的：探究浮力的大小与哪些因素有关
实验过程：如图①，在两个完全相同的溢水杯中，分别盛满甲、乙两种不同密度的液体，将完全相同的两个质地均匀的圆柱体小铝块分别悬挂在弹簧测力计A、B的下方，从离桌面20cm的高度，分别缓慢浸入到甲、乙两种液体中，通过观察弹簧测力计示数的变化，探究浮力大小的变化．（溢水杯的杯底厚度忽略不计）
实验结论：物体在液体中所受浮力的大小，跟它浸在液体中的体积有关、跟液体的密度有关．物体浸在液体中的体积越大、液体的密度越大，浮力就越大．
总结公式：当小铝块位于液面上方时，F_拉力＝G_重力；当小铝块浸入液面后，F_拉力＝G_重力﹣F_浮力．
【建立模型】在实验探究的过程中，实验小组发现：弹簧测力计A ， B各自的示数F_拉力（N）与小铝块各自下降的高度x（cm）之间的关系如图②所示．
【解决问题】

(1)、当小铝块下降10cm时，直接写出弹簧测力计A和弹簧测力计B的示数．

(2)、当6≤x≤10时，求弹簧测力计A的示数F_拉力关于x的函数解析式．

(3)、当弹簧测力计A悬挂的小铝块下降8cm时，甲液体中的小铝块受到的浮力为m（N），若使乙液体中的小铝块所受的浮力也为m（N），则乙液体中小铝块浸入的深度为n（cm），直接写出m ， n的值．

查看试题解析

气体温度 $x (℃)$	…	25	30	35	…
气体体积 $y (L)$	…	596	606	616	…

北师大版数学八年级上册单元分层检测卷第四章 《一次函数》B卷

一、选择题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共8题，共72分）

北师大版数学八年级上册单元分层检测卷第四章《一次函数》B卷