北师大版数学八年级上册单元分层检测卷第四章 《一次函数》A卷
试卷更新日期:2025-11-15 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 点在正比例函数()的图象上,则k的值为( )A、-15 B、15 C、 D、2. 新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远甩在后头.骄傲自满的兔子觉得自己遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用S1、S2分别表示乌龟和兔子赛跑的路程,t为赛跑时间,则下列图象中与故事情节相吻合的是( )A、
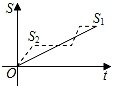 B、
B、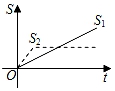 C、
C、 D、
D、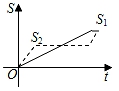 3. 如图,在平面直角坐标系中,点 , 点 , 若将直线向上平移d个单位长度后与线段有交点,则d的取值范围是( )
3. 如图,在平面直角坐标系中,点 , 点 , 若将直线向上平移d个单位长度后与线段有交点,则d的取值范围是( ) A、 B、 C、 D、4. 清明假期,刘老师乘车从学校到井冈山观赏映山红,缅怀革命先烈.已知学校距离井冈山150km,车行驶的平均速度为 , 后刘老师距离井冈山 , 则与之间的关系式是( )A、 B、 C、 D、5. 若函数(k为常数,且)中,随的增大而增大,则其图像可能是( )A、
A、 B、 C、 D、4. 清明假期,刘老师乘车从学校到井冈山观赏映山红,缅怀革命先烈.已知学校距离井冈山150km,车行驶的平均速度为 , 后刘老师距离井冈山 , 则与之间的关系式是( )A、 B、 C、 D、5. 若函数(k为常数,且)中,随的增大而增大,则其图像可能是( )A、 B、
B、 C、
C、 D、
D、 6. 已知一次函数的图象经过第一、二、四象限,则的取值范围是( )A、 B、 C、 D、7. 已知一次函数y-3x+1的图象向上平移t(↑>0)个单位长度后,其图象经过点(2,8),则t的值为( )A、1 B、2 C、3 D、48. 古秤是一种人类智慧的产物,也是华夏文明的瑰宝之一.如图,我们可以用秤砣到秤纽(秤杆上手提的部分)的水平距离得出秤钩上所挂物体的重量,称重时,若秤钩所挂物重为x斤,秤砣到秤纽的水平距离为ycm.下表为若干次称重时所记录的一些数据:
6. 已知一次函数的图象经过第一、二、四象限,则的取值范围是( )A、 B、 C、 D、7. 已知一次函数y-3x+1的图象向上平移t(↑>0)个单位长度后,其图象经过点(2,8),则t的值为( )A、1 B、2 C、3 D、48. 古秤是一种人类智慧的产物,也是华夏文明的瑰宝之一.如图,我们可以用秤砣到秤纽(秤杆上手提的部分)的水平距离得出秤钩上所挂物体的重量,称重时,若秤钩所挂物重为x斤,秤砣到秤纽的水平距离为ycm.下表为若干次称重时所记录的一些数据:
x(斤)
1
2
3
4
5
6
y(cm)
0.75
1
1.25
1.5
1.75
2
在不超重的情况下,当x=9时,对应的水平距离y为( )
A、2.5 B、2.75 C、2.55 D、2.259. 在平面直角坐标系中,一次函数y=mx+b(m,b均为常数)与正比例函数y=nx(n为常数)的图象如图所示,则关于x的方程mx=nx﹣b的解为( ) A、x=3 B、x=﹣3 C、x=1 D、x=﹣110. 甲、乙两车从A城出发前往B城.在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示.则下列说法正确的是( )
A、x=3 B、x=﹣3 C、x=1 D、x=﹣110. 甲、乙两车从A城出发前往B城.在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示.则下列说法正确的是( ) A、甲乙两车在距离B城处相遇 B、甲乙两车同时到达B城,甲车速度是 C、甲车比乙车早出发1小时,乙车的速度是 D、乙车的速度高于甲车,乙车用时4小时从A城到达B城
A、甲乙两车在距离B城处相遇 B、甲乙两车同时到达B城,甲车速度是 C、甲车比乙车早出发1小时,乙车的速度是 D、乙车的速度高于甲车,乙车用时4小时从A城到达B城二、填空题(每题3分,共18分)
-
11. 函数y= 的自变量x的取值范围是 .12. 若点(﹣3,y1)、(2,y2)都在函数y=﹣4x+b的图象上,y1y2(填“>”、“<”、“=”).13. 在平面直角坐标系中,函数和的图象如图所示,则方程的解为 .
 14. 请你写出一个一次函数,满足条件:①经过第一、二、三象限;②与轴的交点坐标为 , 此一次函数的解析式可以是 .15. 如图,在中,点从点出发向点运动,在运动过程中,设表示线段的长,表示的面积,点到的距离为6,则与之间的关系式为: .
14. 请你写出一个一次函数,满足条件:①经过第一、二、三象限;②与轴的交点坐标为 , 此一次函数的解析式可以是 .15. 如图,在中,点从点出发向点运动,在运动过程中,设表示线段的长,表示的面积,点到的距离为6,则与之间的关系式为: . 16. 甲、乙两人赛跑,路程s(m)与时间t(s)之间的关系如图所示,则下列说法正确的是 . (填序号)
16. 甲、乙两人赛跑,路程s(m)与时间t(s)之间的关系如图所示,则下列说法正确的是 . (填序号)
(1)两人赛跑的路程是100m
(2)甲先到达终点
(3)甲跑的平均速度比乙跑的平均速度快0.5m/s
(4)乙跑的平均速度是8m/s
三、解答题(共8题,共72分)
-
17. 小亮骑自行车去上学,当他以往常的速度骑行至点A处时,忽然想起要买某本书,于是又折回到刚经过的一家书店,买到书后继续赶去学校。以下是他本次上学离家距离与时间的关系示意图。根据图中提供的信息回答下列问题:
 (1)、图象所表示的两个变量中,自变量是;因变量是:(2)、小亮家到学校的距离是米;本次上学途中,小亮一共骑行了米;(3)、点A的实际意义是什么?(4)、如果小亮不买书,以往常的速度去学校,从家到学校需要多少分钟?18. 甲、乙两车从A城出发匀速行驶至B城,在整过行驶过程中,甲、乙两车离开A城的距离与甲车行驶时间之间的函数关系如图示.请回答下列问题.
(1)、图象所表示的两个变量中,自变量是;因变量是:(2)、小亮家到学校的距离是米;本次上学途中,小亮一共骑行了米;(3)、点A的实际意义是什么?(4)、如果小亮不买书,以往常的速度去学校,从家到学校需要多少分钟?18. 甲、乙两车从A城出发匀速行驶至B城,在整过行驶过程中,甲、乙两车离开A城的距离与甲车行驶时间之间的函数关系如图示.请回答下列问题. (1)、两城相距 km,甲车的速度是 . 乙车的速度是 .(2)、求乙车追上甲车所用的时间.19. 如图,已知直线的图象经过点 , , 且与x轴交于点C.
(1)、两城相距 km,甲车的速度是 . 乙车的速度是 .(2)、求乙车追上甲车所用的时间.19. 如图,已知直线的图象经过点 , , 且与x轴交于点C. (1)、求直线的解析式;(2)、求的面积.20. 某机动车出发前油箱内有油48L.行驶若干小时后,途中在加油站加油若干升.油箱中剩余油量与行驶时间之间的关系如图所示,根据图象回答下列问题.
(1)、求直线的解析式;(2)、求的面积.20. 某机动车出发前油箱内有油48L.行驶若干小时后,途中在加油站加油若干升.油箱中剩余油量与行驶时间之间的关系如图所示,根据图象回答下列问题. (1)、在这个变化过程中,____________是自变量,______________是因变量;(2)、机动车行驶___________小时后加油,中途加油__________L;(3)、如果加油站距目的地还有360km,车速为 , 要到达目的地,请判断油箱中的油是否够用,并说明理由.21. 已知一次函数y=kx-4,当x=2时,y=-3.
(1)、在这个变化过程中,____________是自变量,______________是因变量;(2)、机动车行驶___________小时后加油,中途加油__________L;(3)、如果加油站距目的地还有360km,车速为 , 要到达目的地,请判断油箱中的油是否够用,并说明理由.21. 已知一次函数y=kx-4,当x=2时,y=-3.(1)求一次函数的表达式;
(2)将该函数的图象向上平移6个单位长度,求平移后的图像与x轴交点的坐标.
22. 甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的关系,请根据图象解答下列问题: (1)、请直接写出点B所对应的数;(2)、轿车到达乙地时,求货车与甲地的距离;(3)、轿车出发多长时间追上货车?23. 随着人工智能的发展,智能机器人送餐成为时尚.某餐厅的机器人聪聪和慧慧,准备从厨房门口出发,给相距的客人送餐.聪聪先出发,且速度保持不变.慧慧待聪聪出发后出发,后将速度提高到原来的倍.设聪聪行走的时间为 , 聪聪和慧慧行走的路程分别为 . , 与x之间的函数图象如图所示.
(1)、请直接写出点B所对应的数;(2)、轿车到达乙地时,求货车与甲地的距离;(3)、轿车出发多长时间追上货车?23. 随着人工智能的发展,智能机器人送餐成为时尚.某餐厅的机器人聪聪和慧慧,准备从厨房门口出发,给相距的客人送餐.聪聪先出发,且速度保持不变.慧慧待聪聪出发后出发,后将速度提高到原来的倍.设聪聪行走的时间为 , 聪聪和慧慧行走的路程分别为 . , 与x之间的函数图象如图所示. (1)、求慧慧提速后的速度;(2)、求图中的与的值.24. 将长为 , 宽为的长方形白纸,按图所示的方法粘合起来,粘合部分宽为
(1)、求慧慧提速后的速度;(2)、求图中的与的值.24. 将长为 , 宽为的长方形白纸,按图所示的方法粘合起来,粘合部分宽为 (1)、根据上图,将表格补充完整.
(1)、根据上图,将表格补充完整.白纸张数
1
2
3
4
5
纸条长度
40
110
145
(2)、设x 张白纸粘合后的总长度为 , 则y 与x 之间的关系式是什么?(3)、你认为多少张白纸粘合起来总长度可能为吗?为什么?