4.5 相似三角形判定定理的证明-北师大版数学九年级上册

试卷更新日期：2025-11-09 类型：同步测试

进入出卷网下载

一、选择题

1. 下列条件中，一定能判定两个等腰三角形相似的是( )

A、都含有一个50°的内角 B、都含有一个70°的内角 C、都含有一个80°的内角 D、都含有一个100°的内角

查看试题解析
2. 如图，在四边形 $A B C D$ 中，已知 $∠ A D C = ∠ B A C$ ，那么补充下列条件后不能判定 $△ A D C$ 和 $△ B A C$ 相似的是（）

A、CA平分 $∠ B C D$ B、 $∠ D A C = ∠ A B C$ C、 $A C^{2} = B C \cdot C D$ D、 $\frac{A D}{A B} = \frac{D C}{A C}$

查看试题解析
3. 已知 $P$ 是 $△ A B C$ 的边 $A C$ 上一点，连接 $B P$ ，则下列不能判定 $△ A B P ∽ △ A C B$ 的是（）

A、 $∠ A B P = ∠ C$ B、 $∠ A P B = ∠ A B C$ C、 $\frac{A B}{A P} = \frac{A C}{A B}$ D、 $\frac{A B}{B P} = \frac{A C}{B C}$

查看试题解析
4. 下列四个三角形中，与如图所示的△ABC 相似的为( )

A、 B、 C、 D、

查看试题解析
5. 在矩形 $A B C D$ 中， $A B = 5$ ， $A D = 3$ ， $E$ ， $F$ 分别是边 $A B$ ， $C D$ 的中点， $C P ⊥ D E$ 于点 $P$ ， $B P$ 的延长线交 $A D$ 于点 $G$ ，则 $G D$ 的长是（）

A、 $\frac{25}{12}$ B、 $2.5$ C、 $3$ D、 $\frac{12}{5}$

查看试题解析
6. 如图，在平面直角坐标系中，矩形OABC 的两边OA，OC 分别在x轴和y轴上，并且OA=5，OC=3.若把矩形OABC 绕着点O逆时针旋转，使点A 恰好落在BC 边上的点A₁处，则点C的对应点 C₁的坐标为( ).

A、 $(- \frac{9}{5}, \frac{12}{5})$ B、 $(- \frac{12}{5}, \frac{9}{5})$ C、 $(- \frac{16}{5}, \frac{12}{5})$ D、 $(- \frac{12}{5}, \frac{16}{5})$

查看试题解析
7. 如图，点 $D$ 为 $△ A B C$ 边 $A C$ 上一点（可与点 $A$ 重合），已知 $A C = 8, B C = 10$ ．以点 $B$ 为圆心，适当长为半径作弧，分别交 $A B, B C$ 于点 $M, N$ ；再以点 $D$ 为圆心， $B M$ 长为半径作弧，交 $A C$ 于点 $P$ （点 $P$ 在点 $D$ 下方）；最后以点 $P$ 为圆心， $M N$ 长为半径作弧，两弧交于点 $Q$ ，连结 $D Q$ 并延长且交 $B C$ 于点 $E$ ．以下 4 个结论：① $∠ C D E = ∠ B$ ；② $\frac{D C}{A C} = \frac{E C}{B C}$ ；③ $C E$ 的最大值为 $\frac{32}{5}$ ；④若 $D$ 为 $A C$ 中点，则 $\frac{B M}{B A} < \frac{2}{5}$ ．其中正确的结论有（）

A、1 个 B、2 个 C、3 个 D、4 个

查看试题解析

二、填空题

8. 如图， $D E ∥ B C$ ，若 $D B = 3$ ， $A B = E C = 5$ ，则 $A E$ 的长为．

查看试题解析
9. 如图，在三角形纸片中，∠A=80°，AB=6，AC=8.将△ABC沿图示中的虚线剪开，剪下的阴影三角形与原三角形相似的有（请在横线上填上符合条件的序号）

查看试题解析
10. 如图，点 B，D，E 在一条直线上，BE 与AC相交于点F， $\frac{A B}{A D} = \frac{B C}{D E} = \frac{A C}{A E} .$ 若∠BAD=21°，则∠EBC 的度数为.

查看试题解析
11. 如图，在平行四边形ABCD中，点E是AB上一点， $\frac{A E}{B E} = \frac{5}{6}$ ，连接DE并延长交CB的延长线于点F.连接CE ，过点A作AG∥EC交DE于点G ，若AG=10，则CE的长为.

查看试题解析
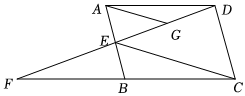12. 在 $△ A B C$ 中， $C A = C B$ ， $A B = 2 \sqrt{3}$ ， $C E ⊥ A B$ ，点D为CB上一点， $D B = 4 C D$ ，连接AD交CE于点M，作 $△ A C D$ 关于AD的对称图形 $△ A C^{'} D$ ，若 $D C^{'} / / C E$ ，则ME为.

查看试题解析

三、解答题

13. 如图， $B D 、 A C$ 相交于点P，连接 $B C 、 A D$ ，且 $∠ 1 = ∠ 2$ ， $A D = 3$ ， $D P = 2$ ， $C P = 1$ ，求 $B C$ 的长．

查看试题解析
14. 如图，在 $△ A B C$ 中， $D$ 是 $A B$ 边上的点，已知 $∠ A D C = ∠ A C B$ ．

(1)、求证： $△ A D C ∽ △ A C B$ ；

(2)、若 $A D = 2$ ， $A C = 3$ ，求 $\frac{S_{△ A C D}}{S_{△ B C D}}$ 的值．

查看试题解析
15. 如图，四边形ABCD中.AC平分∠DAB，∠ADC=∠ACB=90°，E为AB的中点，

(1)、求证： $A C^{2} = A B \cdot A D$ ；

(2)、若 $A D = 4$ ， $A B = 6$ ，求 $\frac{A C}{A F}$ 的值.

查看试题解析
16. 如图，在矩形 ABCD 中，AB =8，AD=4，E 是边DC 上的任一点(不包括端点 D，C)，过点 A 作AF⊥ AE 交CB 的延长线于点 F，设DE=a.

(1)、求BF 的长(用含 a 的代数式表示).

(2)、连结EF 交AB 于点G，连结GC.当GC∥AE 时，求证：四边形 AGCE 是菱形.

查看试题解析
17. 如图， $A B / / C D, A C, B D$ 交于点 $E$ ，过点 $E$ 作 $E F / / A B$ 交 $B C$ 于点 $F$ ．已知 $A E = B C, C E = 3$ ．设 $C F = x, A E = y$ ．

(1)、求 $y$ 关于 $x$ 的函数表达式。

(2)、若 $C F = 2, A B = 8$ ，求 $C D$ 的长．

查看试题解析
18. 如图，在 $△ A B C$ 中，点 $D$ ， $E$ 分别在边 $A B$ ， $A C$ 上，连接 $D E .$ 有以下四个条件： $① ∠ A E D = ∠ B$ ； $② ∠ B D E + ∠ C = 180 °$ ； $③ A D \cdot A B = A E \cdot A C$ ； $④ \frac{A D}{A C} = \frac{D E}{C B}$ ．

(1)、请你从中任选一个条件，使得 $△ A B C$ ∽ $△ A E D$ ，并说明理由．
注：如果选择多个结论分别作答，按第一个解答计分．

(2)、在 $(1)$ 的前提下，若点 $E$ 为 $A C$ 中点， $A E = 2 A D = 6$ ，求线段 $A B$ 的长．

查看试题解析
19. 小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午，他和学习小组的同学带着测量工具来到这棵古树前，由于有围栏保护，他们无法到达古树的底部B，如图所示.于是他们先在古树周围的空地上选择一点D，并在点D处安装了测量器CD，测得 $∠ A C D =135 °$ ；再在BD的延长线上确定一点G，使 $D G = 5$ 米，并在G处的地面上水平放置了一个小平面镜，小明沿着BG方向移动，当移动到点F时，他刚好在小平面镜内看到这棵古树的顶端A的像，此时，测得 $F G = 2$ 米，小明眼睛与地面的距离 $E F =1.6$ 米，测量器的高度 $C D =0.5$ 米.已知点F、G、D、B在同一水平直线上，且EF、CD、AB均垂直于FB，则这棵古树的高度AB为多少米？（小平面镜的大小忽略不计）

查看试题解析
20. 如图（1），在矩形 $A B C D$ 中， $A D = n A B$ ，点M，P分别在边 $A B, A D$ 上（均不与端点重合），且 $A P = n A M$ ，以 $A P$ 和 $A M$ 为邻边作矩形 $A M N P$ ，连接 $A N, C N$ ．
【问题发现】
（1）如图（2），当 $n = 1$ 时， $B M$ 与 $P D$ 的数量关系为_________， $C N$ 与 $P D$ 的数量关系为_________．
【类比探究】
（2）如图（3），当 $n = 2$ 时，矩形 $A M N P$ 绕点A顺时针旋转，连接 $P D$ ，则 $C N$ 与 $P D$ 之间的数量关系是否发生变化？若不变，请就图（3）给出证明；若变化，请写出数量关系，并就图（3）说明理由．
【拓展延伸】
（3）在（2）的条件下，已知 $A D = 4, A P = 2$ ，当矩形 $A M N P$ 旋转至C，N，M三点共线时，请写出线段 $C N$ 的长并说明理由．

查看试题解析
21. 综合与实践

【问题提出】
勾股定理和黄金分割是几何学中的两大瑰宝，其中"贵金分割"给人以美感.课本第56页这样定义"黄金分割点"：如图1，点 $P$ 将线段AB分成两部分 $(A P > B P)$ ，若 $\frac{B P}{A P} = \frac{A P}{A B}$ ，则称点 $P$ 为线段AB的黄金分割点，这个比值称为黄金比.

(1)、【初步感知】
如图1，若 $A B = 1$ ，求临金比 $\frac{A P}{A B}$ 的值.

(2)、【类比探究】
如图2，在 $△ A B C$ 中， $D$ 是BC边上一点，AD将 $△ A B C$ 分割成两个三角形（ $S_{△ A D D} > S_{△ A C D}$ ），若 $\frac{S_{△ A C D}}{S_{△ A B D}} = \frac{S_{△ A B D}}{S_{△ A B C}}$ ，则称AD为 $△ A B C$ 的黄金分割线.
①求证：点D是线段BC的黄金分割点：
②若△ABC的面积为4，求△ACD的面积.

(3)、【拓展应用】
如图3，在 $△ A B C$ 中， $D$ 为A，B上的一点（不与A，B重合），过D作DE∥BC，交AC于E，BE，CD相交于 $F$ ，连接AF并延长，与DE，BC分别交于M，N.请问直线AN是 $△ A B C$ 的黄金分割线吗?并说明理由.

查看试题解析