4.4 探索三角形相似的条件-北师大版数学九年级上册

试卷更新日期：2025-11-09 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，点P是 $△ A B C$ 的边 $A C$ 上一点，连结 $B P$ ，以下条件中，不能判定 $△ A B P ∽ △ A C B$ 的是（）

A、 $∠ A B P = ∠ C$ B、 $∠ A P B = ∠ A B C$ C、 $\frac{A B}{A P} = \frac{A C}{A B}$ D、 $\frac{B P}{C B} = \frac{A B}{A C}$

查看试题解析
2. 如图，已知 $∠ 1 = ∠ 2$ ，那么添加下列一个条件后，不能判定 $△ A B C ~ △ A D E$ 的是（）

A、 $∠ C = ∠ E$ B、 $∠ B = ∠ A D E$ C、 $\frac{A B}{A D} = \frac{A C}{A E}$ D、 $\frac{A B}{A D} = \frac{B C}{D E}$

查看试题解析
3. 已知P为线段 $A B$ 的黄金分割点， $A B = 4$ ， $A P > B P$ ，则 $A P$ 的长为（）

A、 $2 \sqrt{5} - 2$ B、 $2 \sqrt{5} - 4$ C、 $1 + \sqrt{5}$ D、 $6 - 2 \sqrt{5}$

查看试题解析
4. 大自然鬼斧神工，一片小小的树叶，也蕴含着“黄金分割”的美．如图，P为线段AB的黄金分割点（AP＞PB）．如果AB的长度为10cm，那么AP的长度是（）

A、 $(5 \sqrt{5} - 5) c m$ B、 $(15 - 5 \sqrt{5}) c m$ C、6.18cm D、 $(5 \sqrt{5} + 5) c m$

查看试题解析
5. 如图，CD是 $R t △ A B C$ 斜边AB上的中线，过点C作 $C E ⊥ C D$ 交AB的延长线于点E，添加下列条件仍不能判断 $△ C E B$ 与 $△ C A D$ 相似的是( )

A、 $∠ C B A = 2 ∠ A$ B、点B是DE的中点 C、 $C E \cdot C D = C A \cdot C B$ D、 $\frac{C E}{C A} = \frac{B E}{A D}$

查看试题解析
6. 如图，有公共顶点的正方形ABCD和正方形BFGE如图摆放，其中点G恰在CD边的四等分点（CG＜DG），连结BD.则DH：BH为（　　）

A、2：3 B、 $\sqrt{2}$ ：2 C、2 $\sqrt{2}$ ： $\sqrt{17}$ D、15：17

查看试题解析
7. 已知如图，点 C 是线段 AB 的黄金分割点（AC＞BC），则下列结论中正确的是（）

A、AB²＝AC²+BC² B、BC²＝AC•BA C、 $\frac{B C}{A C} = \frac{\sqrt{5} - 1}{2}$ D、 $\frac{A C}{B C} = \frac{\sqrt{5} - 1}{2}$

查看试题解析

二、填空题

8. 如图，已知点 $P$ 是线段 $A B$ 的黄金分割点 $(A P > B P)$ ，若 $A B = 2$ ，则 $A P =$ ．

查看试题解析
9. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $C D ⊥ A B$ ，垂足为 $D$ ，若 $A D = 2$ ， $B D = 1$ ，那么线段 $C D$ 的长为．

查看试题解析
10. 在如图所示的不完整的象棋棋盘(每个小正方形的边长均相等)中，根据“马走日”的规则，要使“马”“车”“炮”所在位置的格点构成的三角形与“帅”“相”“兵”所在位置的格点构成的三角形相似，则“马”应落在处(填序号).

查看试题解析
11. 一个三角形木架的三边长分别是 75 cm，100 cm，120cm，现要再做一个与其相似的三角形木架，而只有长为60cm和120cm的两根木条.要求以其中一根为一边，从另一根上截下两段作为另两边(允许有余料)，则不同的截法有种.

查看试题解析
12. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示．过点D作DF的垂线交小正方形对角线EF的延长线于点G，连结CG，延长BE交CG于点H．若AE＝2BE，则 $\frac{C G}{B H}$ 的值

查看试题解析

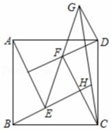
三、解答题

13. 如图，在△ABC中，AB=AC ，点D、B、C、E在同一条直线上，且∠D=∠CAE.

(1)、求证：△ABD∽△ECA；

(2)、若AC=6，CE=4，求BD的长度.

查看试题解析
14. 如图，在Rt△ACB中，∠C=90°，AC=16cm，BC=8cm，动点P从点C出发，沿CA方向运动；动点Q同时从点B出发，沿BC方向运动，如果点P的运动速度为4cm/s，Q点的运动速度为2cm/s，那么运动几秒时，△ABC和△PCQ相似？

查看试题解析
15. 如图，已知 $△ A D E ∽ △ A B C$ ， $D E = 3$ ， $B C = 9$ ．

(1)、求 $\frac{A E}{A C}$ 的值；

(2)、若 $A E = 4$ ，求 $A C$ 的长．

查看试题解析
16. 如图，AB=25，BC=40，AC=20，AE=12，AD=15，DE=24.

(1)、判断△ABC 与△ADE 是否相似.

(2)、若∠BAC=125°，∠EAC=85°，求∠CAD

查看试题解析
17. 如图，在△ABC中，AB=4cm，AC=3cm，BC=6cm，D 是AC 上一点，AD=2cm ，点 P 从点 C 出发沿 C→B→A 的方向，以1cm/s的速度运动至点 A 处，设运动时间为 ts.

(1)、当点 P 在线段 BC 上运动时，BP =；当点 P 在线段AB 上运动时，BP=(用含 t 的代数式表示).

(2)、线段 DP 将△ABC 分成两部分，当其中一部分与△ABC 相似时，求t 的值.

查看试题解析
18. 如图，在 $△ A B C$ 中，点 $D$ ， $E$ 分别在边 $A B$ ， $A C$ 上，连接 $D E$ ．有以下四个条件：① $∠ A E D = ∠ B$ ；② $∠ B D E + ∠ C = 180 °$ ；③ $A D \cdot A B = A E \cdot A C$ ；④ $\frac{A D}{A C} = \frac{D E}{C B}$ ．

(1)、请你从中任选一个条件，使得 $△ A B C ∽ △ A E D$ ，并说明理由．
注：如果选择多个结论分别作答，按第一个解答计分．

(2)、在（1）的前提下，若点 $E$ 为 $A C$ 中点， $A E = 2 A D = 6$ ，求线段 $A B$ 的长．

查看试题解析
19. 某晚，小静在相邻两盏垂直于地面的路灯 $A B$ ， $C D$ 之间行走，点 $A$ ， $C$ 为光源，影子 $P E$ 和 $P F$ 在线段 $B D$ 上，图 $①$ ，图 $②$ 为示意图 $.$ 已知 $A B = C D = 8 m$ ，小静的身高 $O P = 1.6 m$ ， $O P ⊥ B D$ 于点 $P$ ， $B D = 14.4 m$ ．

(1)、如图 $①$ ，当点 $P$ 为 $B D$ 中点时，分别求线段 $P E$ ， $P F$ 的长．

(2)、如图 $②$ ，当点 $P$ 不是 $B D$ 中点时，设 $P E = a$ ，求线段 $P F$ 的长 $. ($ 用含有 $a$ 的代数式表示 $)$

(3)、由此，你觉得 $P E$ 与 $P F$ 存在怎样的数量关系？

查看试题解析
20. 如图1，某小组通过实验探究凸透镜成像的规律，他们依次在光具座上垂直放置发光物箭头、凸透镜和光屏，并调整到合适的高度．如图2，主光轴l垂直于凸透镜 $M N$ ，且经过凸透镜光心O，将长度为8厘米的发光物箭头 $A B$ 进行移动，使物距 $O C$ 为32厘米，光线 $A O 、 B O$ 传播方向不变，移动光屏，直到光屏上呈现一个清晰的像 $A^{'} B^{'}$ ，此时测得像距 $O D$ 为12.8厘米．

(1)、求像 $A^{'} B^{'}$ 的长度．

(2)、已知光线 $A P$ 平行于主光轴l，经过凸透镜 $M N$ 折射后通过焦点F，求凸透镜焦距 $O F$ 的长．

查看试题解析