特殊三角形之三线合一的拓展运用-浙教版数学八年级上册培优训练
试卷更新日期:2025-11-06 类型:复习试卷
一、选择题
-
1. 如图,在中,为AB的中点,为CD上一点,为BC延长线上一点,且.有下列结论:①;②;③为等边三角形;④.其中正确的结论有( )
 A、1个 B、2个 C、3个 D、4个2. 如图,在△ABC中,AC=1,AC边上的中线。过点A作AE⊥BC于点E,记BE长为x,BC长为y。当x,y的值发生变化时,下列代数式的值不变的是( )
A、1个 B、2个 C、3个 D、4个2. 如图,在△ABC中,AC=1,AC边上的中线。过点A作AE⊥BC于点E,记BE长为x,BC长为y。当x,y的值发生变化时,下列代数式的值不变的是( ) A、x+y B、x-y C、xy D、x2+y2
A、x+y B、x-y C、xy D、x2+y2二、填空题
-
3. 如图,在中, , 点D在内,平分 , 连接 , 把沿折叠,落在处,交于F,恰有 . 若 , , 则 .
 4. 如图①,在中, , 动点从点出发,沿折线运动到点 , 速度为 , 其中的长与运动时间的关系如图②.则的面积为 .
4. 如图①,在中, , 动点从点出发,沿折线运动到点 , 速度为 , 其中的长与运动时间的关系如图②.则的面积为 . 5. 如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=4,D是线段AB上一个动点,以BD为边在△ABC外作等边△BDE,若F是DE的中点,连结AF,当CF取最小值时, △ACF的周长为。
5. 如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=4,D是线段AB上一个动点,以BD为边在△ABC外作等边△BDE,若F是DE的中点,连结AF,当CF取最小值时, △ACF的周长为。 6. 如图,在中,是AC边上一点,且 , 连结BD并延长至点 , 使 , 连结AE,若 , 则 , .
6. 如图,在中,是AC边上一点,且 , 连结BD并延长至点 , 使 , 连结AE,若 , 则 , . 7. 如图,A,B,C,D四个点顺次在直线l上, , . 以为底向下作等腰直角三角形 , 以为底向上作等腰三角形 , 且 . 当时,和的面积和是 . 连结 , , 当的长度变化时,与的面积之差保持不变,则a与b需满足的条件是 .
7. 如图,A,B,C,D四个点顺次在直线l上, , . 以为底向下作等腰直角三角形 , 以为底向上作等腰三角形 , 且 . 当时,和的面积和是 . 连结 , , 当的长度变化时,与的面积之差保持不变,则a与b需满足的条件是 .
三、解答题
-
8. 如图,在长方形中, , , 点是边上的一点,且 , 动点从点出发,以的速度沿运动,最终到达点 . 设点运动的时间为秒.
 (1)、当时,长为_____.当点在线段上时,用含的代数式表示长为_____.(2)、当的面积等于时,请求出的值.(3)、在运动过程中,当是等腰三角形时,请求出的值.9. 某兴趣小组在学习了勾股定理之后提出:“锐(钝)角三角形有没有类似于勾股定理的结论”的问题.首先定义了一个新的概念:如图(1)中,是的中点,是射线上的点,设 . 若 , 则称为勾股比.
(1)、当时,长为_____.当点在线段上时,用含的代数式表示长为_____.(2)、当的面积等于时,请求出的值.(3)、在运动过程中,当是等腰三角形时,请求出的值.9. 某兴趣小组在学习了勾股定理之后提出:“锐(钝)角三角形有没有类似于勾股定理的结论”的问题.首先定义了一个新的概念:如图(1)中,是的中点,是射线上的点,设 . 若 , 则称为勾股比.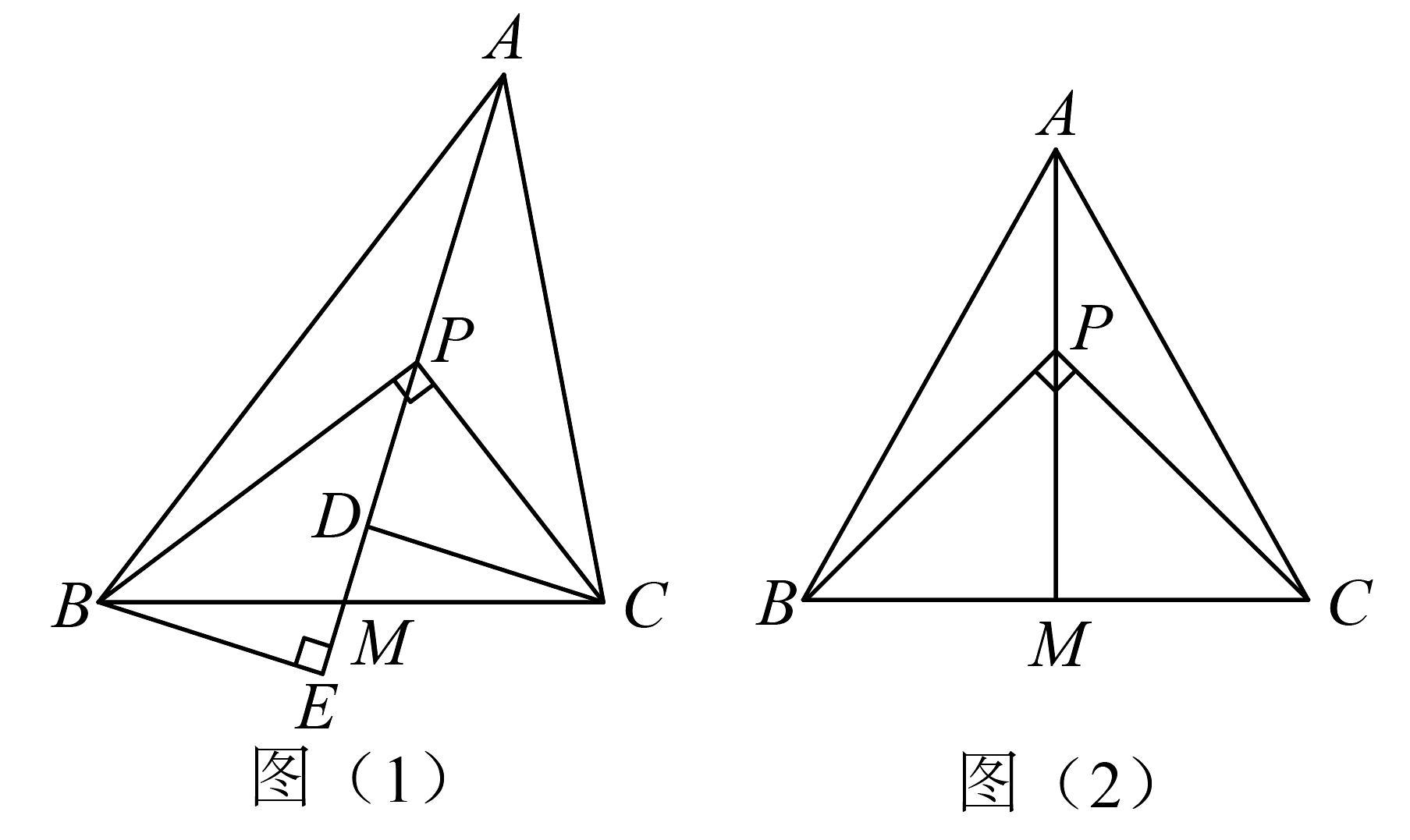 (1)、如图(1),过、分别作中线的垂线,垂足为、 . 求证: .(2)、①如图(2),当 , 且时, (填一个恰当的数).
(1)、如图(1),过、分别作中线的垂线,垂足为、 . 求证: .(2)、①如图(2),当 , 且时, (填一个恰当的数).②如图(1),当 , 为锐角三角形,且时,①中的结论还成立吗?若成立,请写出证明过程;若不成立,也请说明理由.
10. 如图1,等腰三角形中,是边上的中线,延长至点 , 使 , 连结 . (1)、求证:是等腰直角三角形.(2)、如图2,过点作的垂线交于点 , 试判断的形状,并说明理由.(3)、如图3,在(2)的基础上, , 连结 , 若是直角三角形,求的长.11. 如图一,△ABC中,D是BC 的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G, DE⊥DF,交AB于点E,连结EG、EF.
(1)、求证:是等腰直角三角形.(2)、如图2,过点作的垂线交于点 , 试判断的形状,并说明理由.(3)、如图3,在(2)的基础上, , 连结 , 若是直角三角形,求的长.11. 如图一,△ABC中,D是BC 的中点,过点D的直线GF交AC于点F,交AC的平行线BG于点G, DE⊥DF,交AB于点E,连结EG、EF. (1)、求证:BG=CF;(2)、如图二,当∠A=90°时,猜想BE,CF,EF的数量关系,并说明理由;(3)、如图三,在(2)的条件下,当AB=AC时,求证ED=FD.12. 在中,于点O , , , 过点A作于点H , 交于点P .
(1)、求证:BG=CF;(2)、如图二,当∠A=90°时,猜想BE,CF,EF的数量关系,并说明理由;(3)、如图三,在(2)的条件下,当AB=AC时,求证ED=FD.12. 在中,于点O , , , 过点A作于点H , 交于点P . (1)、求线段的长度;(2)、连接 , 求的度数;(3)、如图2,若点D为的中点,点M为线段延长线上一动点,连接 , 过点D作交线段延长线于N点,则的值是否发生改变,如改变,求出该值的变化范围;若不改变,求该式子的值.
(1)、求线段的长度;(2)、连接 , 求的度数;(3)、如图2,若点D为的中点,点M为线段延长线上一动点,连接 , 过点D作交线段延长线于N点,则的值是否发生改变,如改变,求出该值的变化范围;若不改变,求该式子的值.