沪科版数学九年级上册21.4二次函数的应用之实际问题（培优练习）-在线组卷题库

1. 如图，用一块长为50cm、宽为30cm的长方形铁片制作一个无盖的盒子，若在铁片的四个角截去四个相同的小正方形，设小正方形的边长为xcm．
（1）底面的长AB＝　 cm，宽BC＝　 cm（用含x的代数式表示）
（2）当做成盒子的底面积为300cm²时，求该盒子的容积．
（3）该盒子的侧面积S是否存在最大的情况？若存在，求出x的值及最大值是多少？若不存在，说明理由．

查看试题解析

2. 综合与实践：学校数学兴趣小组围绕“校园花圃方案设计”开展主题学习活动.

已知花圃一边靠墙(墙的长度不限)，其余部分用总长为60m的栅栏围成.兴趣小组设计了以下两种方案，设与墙垂直的边的长度为 xm，花圃的面积为 $s m^{2} .$

方案一

方案二

如图1，围成一个矩形花圃.

如图2，围成矩形花圃时，用栅栏(栅栏宽度忽略不计)将该花圃分隔为两个小矩形区域，用来种植不同花卉，并在花圃两侧各留一个宽为3m 的进出口(此处不用栅栏).

(1)、在方案一中，

①求S与x的函数表达式；

②若围成的花圃面积为 $450 m^{2} ，$ ，求与墙垂直的边的长度；

(2)、要使方案二中花圃的面积最大，求与墙平行的边的长度为多少米?

查看试题解析

3. 课本中有一个例题：
有一个窗户形状如图1，上部是一个半圆，下部是一个矩形，如果制作窗框的材料总长为6m，如何设计这个窗户，使透光面积最大？
这个例题的答案是：当窗户半圆的半径约为0.35m时，透光面积最大值约为1.05m² ．
我们如果改变这个窗户的形状，上部改为由两个正方形组成的矩形，如图2，材料总长仍为6m，利用图3，解答下列问题：
（1）若AB为1m，求此时窗户的透光面积？
（2）与课本中的例题比较，改变窗户形状后，窗户透光面积的最大值有没有变大？请通过计算说明．

查看试题解析

4. 一座拱桥的轮廓是抛物线型（如图1），拱高6m，跨度20m，相邻两支柱间的距离均为5m．将抛物线放在所给的直角坐标系中（如图2），

(1)、求抛物线的解析式．求支柱EF的长度．

(2)、拱桥下地平面是双向行车道（正中间是一条宽2m的隔离带），其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车（汽车间的间隔忽略不计）？请说明你的理由．

查看试题解析
5. 如图为石河子某新建住宅小区修建的一个横断面为抛物线的拱形大门，点Q为顶点，其高为8米，宽 $O P$ 为16米．以点O为原点， $O P$ 所在直线为x轴建立直角坐标系．

(1)、求出该抛物线的函数表达式；

(2)、拱形大门下的道路设双向行车道供车辆出入（正中间是宽 $3.2$ 米的值班室），其中的一条行车道能否行驶宽 $2.4$ 米、高 $4.5$ 米的消防车辆？请通过计算说明．

查看试题解析
6. 某公路有一个抛物线形状的隧道ABC，其横截面如图所示，在图中建立的直角坐标系中，抛物线的解析式为y＝﹣ $\frac{1}{10}$ x²+c且过顶点C（0，5）.（长度单位：m）

(1)、直接写出c＝　　；

(2)、求该隧道截面的最大跨度（即AB的长度）是多少米？

(3)、该隧道为双向车道，现有一辆运货卡车高4米、宽3米，问这辆卡车能否顺利通过隧道？请说明理由.

查看试题解析
7. 被誉为“中轴线上第一桥”的万宁桥（如图1），是北京中轴线15个遗产构成要素之一，是中轴线上最古老的桥梁，也是北京市目前唯一还在为社会交通服务的元代桥梁．据记载，元代初建时桥下的净空高度约为6米，其后由于湖底淤积逐渐增高，桥下的净空高度不断减小，遂给人难以通船的感觉．

(1)、假设万宁桥拱截面为抛物线，以抛物线对称轴所在的直线为y轴，建立平面直角坐标系（如图2），求该抛物线的解析式；

(2)、现有一艘游船，其左右两边缘最宽处有一个长方体形状的遮阳棚，此船正对着桥洞在河中航行（如图2）．水面到棚顶的高度为 $2.5$ 米，遮阳棚的宽为4米，问此船能否通过桥洞？请说明理由．

查看试题解析

8. 某地某网店专门销售甲乙两种儿童套装，乙每件的进价比甲多5元，某次用1300元购进两种儿童套装各20件．销售中发现：甲种每天销售件数y（件）与销售单价x（元）之间存在一次函数关系，如图所示．

(1)、求甲种儿童套装每件的进价；

(2)、求y与x之间的函数关系式（不要求写自变量的取值范围）；

(3)、网店每天甲种套装的销售量不低于250件，当甲种套装销售单价为多少元时，每天销售甲种套装获取的利润最大，最大利润是多少？

查看试题解析
9. 某玩具店销售一款玩具，已知该玩具成本为20元，经试销发现，该玩具每天的销售量y（件）与销售单价x（元）之间近似满足函数关系式： $y = - x + 50$ ，为了保证利润，规定 $20 < x < 50$ ．

(1)、当销售单价为30元时，该玩具每天的销售额为多少？（销售额 $=$ 销售量 $\times$ $\times$ 销售单价）

(2)、求销售该玩具每天的利润w（元）的最大值．

(3)、该店为响应“助力防控，回馈社会”活动，决定每卖出一个玩具就捐赠a元（ $1 \leq a \leq 5$ ），若每天扣除捐款后仍可获最大利润196元，则a的值为多少？

查看试题解析

10. 如图1，灌溉车为公路绿化带草坪浇水，图2是灌溉车浇水操作时的截面图．现将灌溉车喷出水的上、下边缘线近似地看作平面直角坐标系 $x O y$ 中两条抛物线的部分图象．已知喷水口H离地竖直高度 $O H$ 为 $1.2 m$ ，草坪水平宽度 $D E = 3 m$ ，竖直高度忽略不计.上边缘抛物线最高点A离喷水口的水平距离为 $2 m$ ，高出喷水口 $0 .4m$ ，下边缘抛物线是由上边缘抛物线向左平移 $4m$ 得到的，设灌溉车到草坪的距离 $O D$ 为d（单位：m）．

(1)、求上边缘抛物线的函数解析式，并求喷出水的最大射程 $O C$ 的长；

(2)、下边缘抛物线落地点B的坐标为______；

(3)、要使灌溉车行驶时喷出的水能浇灌到整个草坪，d的取值范围为______．

查看试题解析
11. 如图1，一辆灌溉车正为绿化带浇水，喷水口 $H$ 离地面竖直高度为 $h = 1.2$ 米，建立如图2所示的平面直角坐标系，可以把灌溉车喷出水的上、下边缘抽象为两条抛物线的部分图象，把绿化带横截面抽象为矩形 $D E F G$ ，其水平宽度 $D E = 2$ 米，竖直高度 $E F = 0.8$ 米，若下边缘抛物线是由上边缘抛物线向左平移得到的，上边缘抛物线最高点 $A$ 离喷水口的水平距离为2米，高出喷水口0.4米，灌溉车到绿化带的距离 $O D$ 为 $d$ 米．

(1)、求上边缘抛物线的函数解析式：

(2)、求下边缘抛物线与x轴交点B的坐标；

(3)、若 $d = 3.2$ 米，则灌溉车行驶时喷出的水（填“能”或“不能”）浇灌到整个绿化带．

查看试题解析
12. 如图1，一辆灌溉车正为绿化带浇水，喷水口 $H$ 离地面竖直高度为 $h = 1.2$ 米，建立如图2所示的平面直角坐标系，可以把灌溉车喷出水的上、下边缘抽象为两条抛物线的部分图象，把绿化带横截面抽象为矩形 $D E F G$ ，其水平宽度 $D E = 2$ 米，竖直高度 $E F = 0.8$ 米，若下边缘抛物线是由上边缘抛物线向左平移得到的，上边缘抛物线最高点 $A$ 离喷水口的水平距离为2米，高出喷水口0.4米，灌溉车到绿化带的距离 $O D$ 为 $d$ 米．

(1)、求上边缘抛物线的函数解析式；

(2)、求下边缘抛物线与 $x$ 轴交点 $B$ 的坐标；

(3)、若 $d = 3.2$ 米，则灌溉车行驶时喷出的水能否浇灌到整个绿化带？

查看试题解析
13. 如图 1，公园草坪的地面 $O$ 处有一根直立水管，喷水口可上下移动，喷出的抛物线形水线也随之上下平移，图 2 是其示意图. 开始喷水后，若喷水口在 $O$ 处，水线落地点为 $A$ ，若喷水口上升到 $P$ 处，水线落地点为 $B$ ，记 $O P$ 长度为 $ℎ$ 。

(1)、已知 $O A = 4 m$ . 若喷水口在 $P$ 处， $ℎ = 1.5 m, O B = 6 m$ .
①求水线最高点与点 $B$ 之间的水平距离；
②求水线的最大高度；
③身高 1.5 m 的小红要从水线下某点经过，为了不被水喷到，该点与 $O$ 的水平距离应满足什么条件？请说明理由.

(2)、在喷水口上升过程中，当 $O B = 2 O A$ 时，用含 $ℎ$ 的式子表示水线的最大高度.

查看试题解析

14. 如图，点 $E$ ， $F$ ， $G$ ， $H$ 分别在菱形 $A B C D$ 的四条边上， $B E = B F = D G = D H$ ，连接 $E F$ ， $F G$ ， $G H$ ， $H E$ ，得到四边形 $E F G H$ ， $∠ A = 60 °$ ．设四边形 $E F G H$ 的面积为 $S$ ， $A E$ 的长为 $x$ ，若 $S$ 关于 $x$ 的函数图象如图所示，则 $A B$ 的长为．

查看试题解析
15. 如图，正方形 $A B C D$ 的边长为4，点 $P$ ， $Q$ 分别是边 $A B$ ， $B C$ 上的动点（不与端点重合），且 $B Q = A P$ ；点 $R$ ， $S$ 分别是边 $C D$ ， $D A$ 上的点， $C R = 1$ ， $D S = 2$ ，设 $A P$ 的长度为 $x$ ，四边形 $P Q R S$ 的面积为 $y$ ．

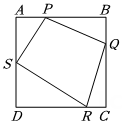(1)、求 $y$ 关于 $x$ 的函数表达式及自变量的取值范围；

(2)、四边形 $P Q R S$ 的面积有没有最值？如果有，请说明是最大值还是最小值，并计算此时 $A P$ 长度，如果没有，请说明理由．

查看试题解析
16. 如图，菱形ABCD中，AB=1，∠A=60°，EFGH是矩形，矩形的顶点都在菱形的边上．设AE=AH=x（0＜x＜1），矩形的面积为S．
（1）求S关于x的函数解析式；
（2）当EFGH是正方形时，求S的值．

查看试题解析
17. 如图，在矩形 $A B C D$ 中， $A B = 3$ ， $B C = 4$ ，点E，F，G，H分别在边 $A B$ ， $B C$ ， $C D$ ， $D A$ 上，且 $D G = B E$ ， $A H = C F = 2 B E$ ，记四边形 $E F G H$ 的面积为y，边长 $B E$ 为x．

(1)、求y关于x的表达式及自变量x的取值范围．

(2)、求y的最小值．

查看试题解析

沪科版数学九年级上册21.4二次函数的应用之实际问题（培优练习）

一、面积问题

二、过车船问题

三、利润问题

四、农业灌溉问题

五、与四边形相关问题（列出函数表达式）