沪科版数学九年级上册21.4二次函数的应用之抛物线型问题（专项练习）

试卷更新日期：2025-11-06 类型：同步测试

进入出卷网下载

一、喷泉问题

1. 如图，一个圆形喷水池的中央竖直安装了一个柱形喷水装置OM ，喷头M向外喷水，水流在各个方向上沿形状相同的抛物线路径落下，按如图所示的直角坐标系，水流喷出的高度y(m)与水平距离x(m)之间的关系式是 $y = - x^{2} + 2 x + \frac{7}{4} (x⟩ 0) ，$ 则水流喷出的最大高度是( )

A、3m B、2.75m C、2m D、1.75m

查看试题解析
2. 某游乐场的圆形喷水池中心O有一雕塑OA，从A点向四周喷水，喷出的水柱为抛物线，且形状相同．如图，以水平方向为x轴，点O为原点建立直角坐标系，点A在y轴上，x轴上的点C，D为水柱的落水点，水柱所在抛物线（第一象限部分）的函数表达式为 $y = - \frac{1}{6} {(x - 5)}^{2} + 6$ ．

(1)、求雕塑高OA．

(2)、求落水点C，D之间的距离．

(3)、若需要在OD上的点E处竖立雕塑EF，OE＝10m，EF＝1.8m，EF⊥OD．问：顶部F是否会碰到水柱？请通过计算说明．

查看试题解析
3. 玥玥看到一处喷水景观，喷出的水柱呈抛物线形状，她对此展开研究：发现水柱距地面的高度 $y (m)$ 与水柱距喷水头的水平距离 $x (m)$ 之间近似满足函数关系 $y = - \frac{1}{10} {(x - h)}^{2} + k$ 的图象，已知水柱在距喷水头 $P$ 水平距离 $5 m$ 处达到最高，最高点距离地面 $3.2 m$ ．身高 $1.6 m$ 的玥玥站在水柱正下方，且距喷水头 $P$ 水平距离 $8 m$ 的位置，她的头顶碰到水柱．（填“能”或“不能”）

查看试题解析
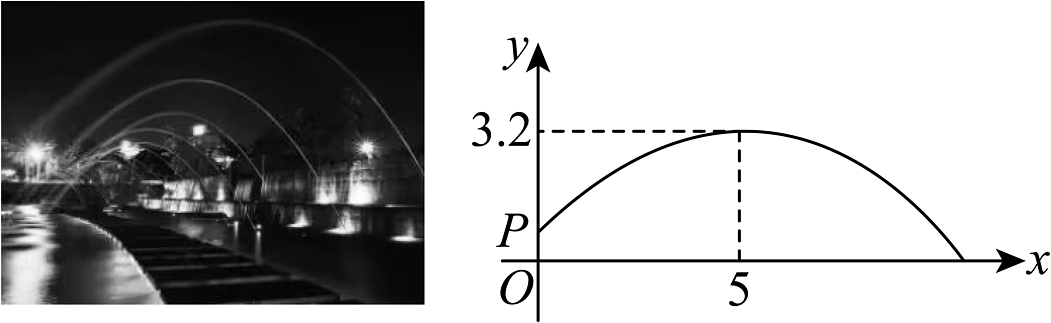4. 2024年巴黎奥运会8月6日单人10米决赛中，全红婵以425.60分的总分夺得金牌，陈芋汐获得银牌，在精彩的比赛过程中，全红婵选择了一个极具难度的 $207 C$ （向后翻腾三周半抱膝），如图2所示，建立平面直角坐标系 $x O y$ ，如果她从点A起跳后的运动路线可以看作抛物线的一部分，从起跳到入水的过程中，她的竖直高度y（单位：米）与水平距离x（单位：米）近似满足二次函数关系．

(1)、在平时训练完成一次跳水动作时，全红婵的水平距离x与竖直高度y的几组数据如下表：
水平距离x/m
3
h
4
4.5
竖直高度y/m
10
11.25
10
6.25
根据表中数据，直接写出h的值为，满足的二次函数关系式为：；

(2)、在（1）的条件下，记全红婵训练时入水点的水平距离为 $d_{1}$ ；比赛当天的某一次跳水中，全红婵的竖直高度y与水平距离x近似满足二次函数关系： $y = - 5 x^{2} + 40 x - 68$ ，记比赛当天入水点的水平距离为 $d_{2}$ ，判断 $d_{1}$ 与 $d_{2}$ 的大小关系，并说明理由．

查看试题解析
5. 背景材料：某社区准备改造原半径为 $6 m$ 的水池中的喷泉设施（如图①），综合实践小组开展了优化设计方案的综合实践活动．

(1)、【建模分析】
如图②，该小组把喷泉最外侧水流抽象成抛物线，测量出如下数据：喷水口位置在水池中心点 $O$ 的正上方且竖直高度为 $2.25 m$ ，水流最高高度为 $3 m$ ，水流最高点距喷水管的水平距离为 $1 m$ ．
任务1：以水池中心点 $O$ 为原点，水平向右方向为 $x$ 轴正半轴，以喷水管竖直向上方向为 $y$ 轴正半轴，建立平面直角坐标系：求原喷泉水流右支抛物线的函数表达式，并计算喷泉水流到喷水管的最大水平距离．

(2)、【优化设计】
社区要求：为了使喷泉喷出的水流达到美观效果，要求喷出的水流所在抛物线最大高度 $A B$ 与水平宽度 $B C$ 的比接近黄金比 $0.618$ ．
如图③，该小组进一步提出优化设计，若优化后水流离喷水管最大水平距离为 $5.5 m$ ，喷水口的竖直高度为 $1.1 m$ ，喷出的水流的最高高度为 $3.6 m$ ．
任务2：求进一步优化后喷出的水流所在抛物线的函数表达式，并通过计算说明该小组所设计喷泉的是否达到美观效果．

查看试题解析

二、涵洞拱桥问题

6. 如图，是一座古拱桥的截面图，拱桥桥洞的上沿是抛物线形状，当水面的宽度为10m时，桥洞与水面的最大距离是5m.因上游水库泄洪，水面宽度变为6m，则水面上涨的高度是m.

查看试题解析
7. 某湖面上有一座抛物线形拱桥，按如图所示的方式建立平面直角坐标系，得到抛物线的函数解析式为 $y = - \frac{1}{16} x^{2}$ ，正常水位时，水面宽 AB 为 16m，此时拱顶 O 到水面 AB 的距离为（）

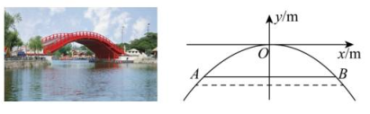A、4m B、3m C、2m D、1m

查看试题解析

8. 根据以下素材，探索完成任务．

如何设计拱桥景观灯的悬挂方案？
素材 $1$	图 $1$ 中有一座拱桥，图 $2$ 是其抛物线形桥拱的示意图，某时测得水面宽 $20 m$ ，拱顶距离水面 $5 m .$ 据调查，该河段水位在此基础上再涨 $1.8 m$ 达到最高．
素材 $2$	为迎佳节，拟在如图 $1$ $1$ 所示的桥洞前面的桥拱上悬挂 $40 c m$ $40 c m$ 长的灯笼，如图 $3 .$ $3 .$ 为了安全，灯笼底部距离水面不小于 $1 m$ $1 m$ ；为了实效，相邻两盏灯笼悬挂点的水平间距均为 $1.6 m$ $1.6 m$ ；为了美观，要求在符合条件处都挂上灯笼，且挂满后成轴对称分布．
问题解决
任务 $1$	确定桥拱形状	在图 $2$ 中建立合适的平面直角坐标系，求抛物线的函数表达式．
任务 $2$	探究悬挂范围	在你所建立的坐标系中，仅在安全的条件下，确定悬挂点纵坐标的最小值和横坐标的取值范围．
任务 $3$	拟定设计方案	给出一种符合所有悬挂条件的灯笼数量，并根据你所建立的坐标系，求出最左边一盏灯笼悬挂点的横坐标．

查看试题解析

三、斜抛运动

9. 某校购买了一套乒乓球桌和自动发球机，侧面如图1所示，球台长度AB＝274cm，发球机紧贴球台端线点A处，高出球台的部分AC＝12cm，出球管道 $C D = 5 \sqrt{2} cm$ ，若将水平状态的CD绕点C逆时针旋转45°到CD的位置，发球机模式为“一跳球”，路线呈抛物线，离球台正中间的球网GH左侧72cm处到达最高点高出台面21cm，则 $E B =$ cm．

查看试题解析

10. 根据以下素材，探索完成任务．

如何确定防守方案？

素材1

鹰眼系统能够追踪、记录和预测球的轨迹，如图分别为足球比赛中某一时刻的鹰眼系统预测画面（如图1）和截面示意图（如图2），足球的飞行轨迹可看成抛物线．攻球员位于 $O$ ，守门员位于点 $A$ ， $O A$ 的延长线与球门线交于点 $B$ ，且点 $A$ ， $B$ 均在足球轨迹正下方，已知 $O B = 28 m$ ， $A B = 8 m$ ．

素材2

通过鹰眼系统监测，足球飞行的水平速度为 $15 m/s$ 水平距离 $s$ （水平距离=水平速度×时间）与离地高度 $h$ 的鹰眼数据如右表．

守门员的最大防守高度为 $\frac{25}{9} m$ ．守门员在攻球员射门瞬间就作出防守反应，当守门员位于足球正下方时，足球离地高度不大于守门员的最大防守高度视为防守成功．

$s /m$	…	9	12	15	18	21	…
$h /m$	…	$4.2$	$4.8$	5	$4.8$	$4.2$	…

问题解决

任务1

确定运动轨迹

求 $h$ 关于 $s$ 的函数表达式．

任务2

探究防守方案

若守门员选择原地接球，能否防守成功？若成功，请求出守门员接住球时，球的高度；若不成功，请通过计算说明理由．

任务3

拟定执行计划

求守门员选择面对足球后退，计算成功防守的最小速度．

查看试题解析

11. 如图，一小球从斜坡O点以一定的方向弹出球的飞行路线可以用二次函数 $y = a x^{2} + b x (a < 0)$ 刻画，斜坡可以用一次函数 $y = \frac{1}{4} x$ 刻画，小球飞行的水平距离x（米）与小球飞行的高度y（米）的变化规律如下表：
x
0
1
2
m
4
5
6
7
…
y
0
$\frac{7}{2}$
6
$\frac{15}{2}$
8
$\frac{15}{2}$
n
$\frac{7}{2}$
…

(1)、① $m =$ ______， $n =$ ______；
②小球的落点是A，求点A的坐标．

(2)、小球飞行高度y（米）与飞行时间t（秒）满足关系 $y = - 5 t^{2} + v t$ ．
①小球飞行的最大高度为______米；
②求v的值．

查看试题解析
12. 为了增加趣味性，万岁山旅游城把传统的抛绣球项目进行改良，他们定制了一种器械，类似中国古代一种投石器，为了解发射平台高度对绣球飞行轨迹的影响，我们可以设定不同的发射平台高度，并分别记录绣球在不同水平距离上的飞行高度. 分析不同发射平台高度下绣球的飞行轨迹. 通过比较不同高度下绣球的飞行高度和飞行距离，我们可以得出发射平台高度对绣球运动轨迹的具体影响. 从而有目的地调整发射高度，通过实验发现绣球运动轨迹是抛物线的一部分，并且在离发射点水平距离18米处达到距地面最大高度18米；在离发射点水平距离6米处，距地面高度10米.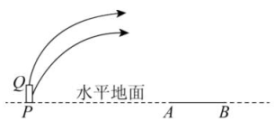
问题解决：

(1)、任务1：确定函数表达式. 设绣球离发射点水平距离为x，距地面高度为y. 求出y关于x的函数表达式；

(2)、任务2：探究飞行距离，当绣球从地面发出到落地（高度为0m）时，飞行的水平距离是多少；

(3)、任务3：如图，工作人员在水平地面上设置一个高度可以变化的发射平台PQ，当弹射口高度变化时，绣球被弹出后的飞行轨迹形状不变，可视为抛物线上下平移得到，点P、A、B在一条直线上，已知 $A P = 37 m$ ， $A B = 1 m$ ，游客小李站在线段AB（包括点A、B）上，为了确保他能抢到绣球，求发射台PQ的变化范围.

查看试题解析
13. 【问题背景】
水火箭是一种基于水和压缩空气的简易火箭，通常由塑胶汽水瓶作为火箭的箭身，并把水当作喷射剂．图 $1$ 是某学校兴趣小组制做出的一款简易弹射水火箭．
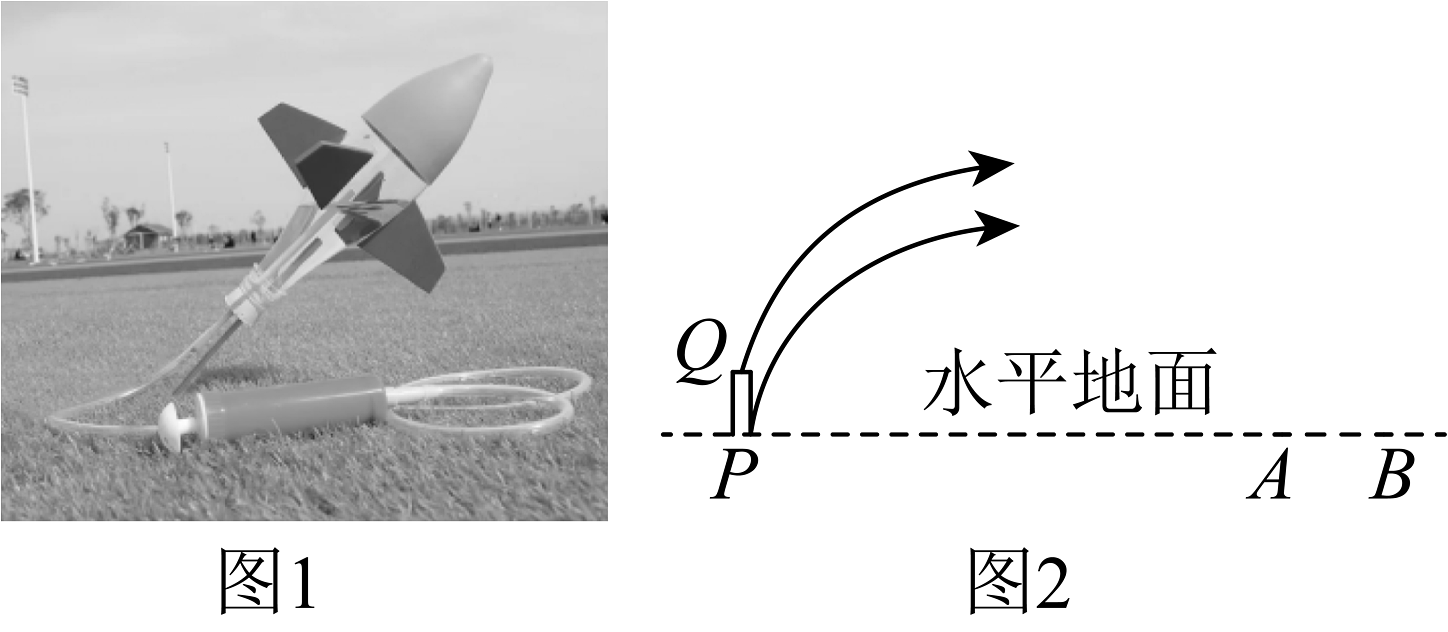
【实验操作】
为验证水火箭的一些性能，兴趣小组同学通过测试收集了水火箭相对于出发点的水平距离 $x$ （单位： $m$ ）与飞行时间 $t$ （单位： $s$ ）的数据，并确定了函数表达式为： $x = 3 t$ ．同时也收集了飞行高度 $y$ （单位： $m$ ）与飞行时间 $t$ （单位： $s$ ）的数据，发现其近似满足二次函数关系．数据如表所示：
飞行时间 $t / s$
$0$
$2$
$4$
$6$
$8$
$\dots$
飞行高度 $y / m$
$0$
$10$
$16$
$18$
$16$
$\dots$
【建立模型】
任务 $1$ ：求 $y$ 关于 $t$ 的函数表达式．
【反思优化】
图 $2$ 是兴趣小组同学在室内操场的水平地面上设置一个高度可以变化的发射平台（距离地面的高度为 $P Q$ ），当弹射高度变化时，水火箭飞行的轨迹可视为抛物线上下平移得到，线段 $A B$ 为水火箭回收区域，已知 $A P = 42 m$ ， $A B = (18 \sqrt{2} - 24) π$ ．
任务 $2$ ：探究飞行距离，当水火箭落地（高度为 $0 m$ ）时，求水火箭飞行的水平距离．
任务 $3$ ：当水火箭落到 $A B$ 内（包括端点 $A$ ， $B$ ），求发射台高度 $P Q$ 的取值范围．

查看试题解析

x	0	1	2	m	4	5	6	7	…
y	0	$\frac{7}{2}$	6	$\frac{15}{2}$	8	$\frac{15}{2}$	n	$\frac{7}{2}$	…

飞行时间 $t / s$	$0$	$2$	$4$	$6$	$8$	$\dots$
飞行高度 $y / m$	$0$	$10$	$16$	$18$	$16$	$\dots$

水平距离x/m	3	h	4	4.5
竖直高度y/m	10	11.25	10	6.25