苏科版数学八年级上册3.3勾股定理的简单应用专项练习-在线组卷题库

1. 如图，在波平如镜的湖面上，有一朵盛开的美丽的红莲，它高出水面3尺．突然一阵大风吹过，红莲被吹至一边，花朵刚好齐及水面，如果知道红莲移动的水平距离为6尺，则水深（　　）尺．

A、3.5 B、4 C、4.5 D、5

查看试题解析
2. 九章算术中记载了一个“折竹抵地”问题：今有竹高一丈，末折抵地，去本三尺，问折者高几何？题意是：一根竹子原高1丈（1丈 $= 10$ 尺），中部有一处折断，竹稍触地面处离竹根4尺，试问折断处离地面多高？则折断处离地面的高度为（）

A、4.55尺 B、5.45尺 C、4.2尺 D、5.8尺

查看试题解析
3. 《九章算术》内容丰富，与实际生活联系紧密，在书上讲述了这样一个问题“今有垣高一丈。倚木于垣，上与垣齐、引木却行一尺、其木至地。问木长几何？”其内容可以表述为：“有一面墙，高1丈将一根木杆斜靠在墙上，使木杆的上端与墙的上端对齐，下端落在地面上．如果使木杆下端从此时位置向远离墙的方向移动1尺，则木杆上端恰好沿着墙滑落到地面上．问木杆长多少尺？”（说明1丈 $=$ 10尺）设木杆长x尺，依题意，下列方程正确的是（）

A、 $x^{2} = {(x - 1)}^{2} + 1^{2}$ B、 ${(x + 1)}^{2} = x^{2} + 10^{2}$ C、 $x^{2} = {(x - 1)}^{2} + 10^{2}$ D、 ${(x + 1)}^{2} = x^{2} + 1^{2}$

查看试题解析
4. 今有池方一丈，葭生其中央，出水一尺.引葭赴岸，适与岸齐.问：水深、葭长各几何?(选自《九章算术》)
题目大意：有一个水池，水面是一个边长为1丈①的正方形.在水池正中央有一根新生的芦苇，它高出水面1尺(如图).如果把这根芦苇垂直拉向岸边，那么它的顶端恰好到达岸边的水面.这个水池的深度和这根芦苇的长度各是多少?
（① “尺”“丈”是我国传统长度单位，1丈=10尺.）

查看试题解析
5. 如图在平静的湖面上，有一支红莲 $B A$ ，高出水面的部分 $A C$ 为1米，一阵风吹来，红莲被吹到一边，花朵齐及水面（即 $A B = D B$ ），已知红莲移动的水平距离 $C D$ 为3米，则湖水深 $C B$ 为多少？

查看试题解析

6. 如图，某沿海城市 $A$ 接到台风预警，在该市正南方向 $340 km$ 的 $B$ 处有一台风中心，沿 $B C$ 方向以 $10 km/h$ 的速度移动，已知城市 $A$ 到 $B C$ 的距离 $A D$ 为 $160 km$ ．

(1)、台风中心经过多长时间从 $B$ 点移到 $D$ 点？

(2)、如果在距台风中心 $B$ 的 $200 km$ 的圆形区域内都将受到台风的影响，那么 $A$ 市受到台风影响的时间持续多少小时？

查看试题解析
7. 森林火灾是一种常见的自然灾害，危害很大，随着中国科技、经济的不断发展，开始应用飞机洒水的方式扑灭火源．如图，有一台救火飞机沿东西方向 $A B$ ，由点A飞向点B，已知点C为其中一个着火点，且点C与直线 $A B$ 上两点 A，B的距离分别为 $300 m$ 和 $400 m$ ，又 $A B = 500 m$ ，飞机中心周围 $260 m$ 以内可以受到洒水影响．

(1)、着火点C 受洒水影响吗？为什么？

(2)、若飞机的速度为 $10 m / s$ ，要想扑灭着火点C估计需要13秒，请你通过计算判断着火点C能否被扑灭？

查看试题解析
8. 森林火灾是一种常见的自然灾害，危害很大，随着中国科技、经济的不断发展，开始应用飞机洒水的方式扑灭火源．如图，有一台救火飞机沿东西方向 $A B$ ，由点 $A$ 飞向点 $B$ ，已知点 $C$ 为其中一个着火点，已知 $A B = 1000 m$ ， $A C = 600 m$ ， $B C = 800 m$ ，飞机中心周围 $500 m$ 以内可以受到洒水影响．

(1)、在飞机飞行过程中，求飞机距离着火点 $C$ 的最短距离；

(2)、若该飞机的速度为 $14 m/s$ ，要想扑灭着火点 $C$ 估计需要15秒，请你通过计算说明着火点 $C$ 能否被飞机扑灭．

查看试题解析

9. 某校为加强学生劳动教育，将劳动基地按班级进行分配，如图是八年级劳动实践基地的示意图形状，经过同学共同努力，测得 $A B = 4 m$ ， $A D = 3 m$ ， $B C = 12 m$ ， $C D = 13 m$ ， $∠ A = 90 °$ ．

(1)、求B、D之间的距离；

(2)、求四边形 $A B C D$ 的面积．

查看试题解析
10. 四川的人民渠（利民渠、幸福渠、官渠堰）是都江堰扩灌工程之一，也是四川省建成的第一座大型水利工程，有“巴蜀新春第一渠”之称．现为扩建开挖某段干渠，如图，欲从干渠某处A向C地、D地、B地分流（点C，D，B位于同一条直线上），修三条笔直的支渠 $A C$ ， $A D$ ， $A B$ ，且 $A C ⊥ B C$ ；再从D地修了一条笔直的水渠 $D H$ 与支渠 $A B$ 在点H处连接，且水渠 $D H$ 和支渠 $A B$ 互相垂直，已知 $A C = 6 km$ ， $A B = 10 km$ ， $B D = 5 km$ ．

(1)、求支渠 $A D$ 的长度．（结果保留根号）

(2)、若修水渠 $D H$ 每千米的费用是 $0.7$ 万元，那么修完水渠 $D H$ 需要多少万元？

查看试题解析
11. 综合与实践
问题情境：某小区的社区管理人员计划在临街的拐角建造一块绿化地（阴影部分），现面向小区居民征集设计方案，欣欣和强强合作一起完成了绿化地和引水灌溉方案的设计．
欣欣设计的绿化地及浇灌点方案如下：如图， $A B = 9 m, B C = 12 m, C D = 17 m, A D = 8 m$ ，在 $C D$ 上选取两点E ， F为浇灌点，从水源点G处铺设管道引水．
强强设计的铺设管道方案如下：
方案一：从水源点G处直接铺设管道分别到浇灌点E ， F；
方案二：过点G作 $C D$ 的垂线，垂足为H ，先从水源点G处铺设管道到点H处，再从点H处分别向浇灌点E ， F铺设管道．
社区管理人员按照欣欣设计的绿化地及浇灌点方案施工，施工人员在只有卷尺的情况下，通过测量某两点之间的距离，就确定了 $∠ A B C = 90 °$ ．

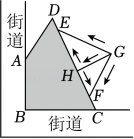(1)、施工人员测量的是点与点之间的距离．

(2)、若绿化地建造每平方米的费用为100元，求建造绿化地的费用．

(3)、若 $∠ E G F = 90 °$ ， $E F = 10 m, E G = 8 m$ ，管道铺设费用为50元/米，请比较强强设计的两种铺设管道方案所花的费用，并求出铺设管道所需的最少费用．

查看试题解析
12.

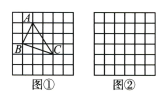(1)、问题背景
在△ABC 中，AB，BC，AC 三边的长分别为 $\sqrt{5} ， \sqrt{10} ， \sqrt{13} ，$ 求这个三角形的面积.小辉同学在解答这道题时，先建立一个正方形网格(每个小正方形的边长为1)，再在网格中画出格点△ABC(即△ABC 三个顶点都在小正方形的顶点处)，如图①所示.这样不需求△ABC 的高，而借用网格就能计算出它的面积.
请你将△ABC 的面积直接填写在横线上：.

(2)、思维拓展
我们把上述求△ABC 面积的方法叫作构图法，若△ABC 三边的长分别为 $\sqrt{5} a ， 2 \sqrt{2} a ， \sqrt{17} a (a⟩ 0) ，$ 请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC，并求出它的面积.

(3)、探索创新
若△ABC三边的长分别为 $\sqrt{m^{2} + 16 n^{2}} ， \sqrt{9 m^{2} + 4 n^{2}} ，$ $2 \sqrt{m^{2} + n^{2}} (m⟩ 0 ， n > 0 ，$ 且m≠n)，试运用构图法求出这个三角形的面积.

查看试题解析

13. 如图所示，在一次消防演习中，消防员架起一架25米长的云梯，斜靠在一面墙上，梯子底端C离墙24米．

(1)、这个梯子的顶端A距地面有多高？

(2)、如果消防员接到命令，要求梯子的顶端上升8米（云梯长度不变），那么云梯底端在水平方向应滑动多少米？

查看试题解析
14. 如图，在离水面高度为8米的岸上，有人用绳子拉船靠岸，开始时绳子 $B C$ 的长为17米，此人以1米/秒的速度收绳，7秒后船移动到点 $D$ 的位置，问船向岸边移动了多少米？（假设绳子一直保持是直的）

查看试题解析
15. 春秋季节筑城广场放风筝已经成为贵阳市的一道靓丽风景线，某校八年级的两位同学学习了“勾股定理”之后，想要测得风筝的垂直高度 $C E$ ，他们进行了如下操作：①测得水平距离 $B D$ 的长为5米；②根据手中剩余线的长度计算出风筝线 $B C$ 的长为13米；③牵线放风筝的小明的身高为1.5米．

(1)、求风筝的垂直高度 $C E$ ；

(2)、如果小明想让风筝沿 $C D$ 方向下降2米，则他应该往回收线多少米？

查看试题解析
16. 综合实践
【问题情境】
某消防队在一次应急演练中，消防员架起一架长 $25 m$ 的云梯 $A B$ ，如图，云梯斜靠在一面墙上，这时云梯底端距墙脚的距离 $B C = 7 m ， ∠ D C E = 90 °$ ．

(1)、【独立思考】
这架云梯顶端距地面的距离 $A C$ 有多高？

(2)、【深入探究】
消防员接到命令，按要求将云梯从顶端A下滑到 $A^{'}$ 位置上（云梯长度不改变）， $A A^{'} = 4 m$ ，那么梯子的底端下滑的距离 $B B^{'}$ 是多少米？

(3)、【问题解决】
在演练中，高 $24 m$ 的墙头有求救声，消防员需调整云梯去救援被困人员，经验表明，云梯靠墙摆放时，如果云梯底端离墙的距离不小于云梯长度的 $\frac{1}{5}$ ，则云梯和消防员相对安全．在相对安全的前提下，云梯的顶端能否到达 $24 m$ 高的墙头去救援被困人员？

查看试题解析

17. 如图，在一条东西走向河流的一侧有一村庄C，河边原有两个取水点A，B，其中AB＝AC，由于某种原因，由C到A的路现在已经不通，该村为方便村民取水决定在河边新建一个取水点H（A、H、B在同一条直线上），并新修一条路CH，测得CB＝1.5千米，CH＝1.2千米，HB＝0.9千米.

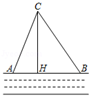(1)、问CH是否为从村庄C到河边的最近路？请通过计算加以说明；

(2)、求新路CH比原路CA少多少千米？

查看试题解析
18. 我们根据图形的移、拼、补可以简单直观地推理验证数学规律和公式，这种方法称之为“无字证明”，它比严谨的数学证明更为优雅与有条理．三国时代东吴数学家赵爽（字君卿，约公元3世纪）在《勾股圆方图注》一书中用割补的方法构造了“无字证明”图形（如图①）．其中四个直角三角形较长的直角边长都为a ，较短的直角边长都为b ，斜边长都为c ，大正方形的面积可以表示为c² ，也可以表示为4× $\frac{1}{2}$ ab+（a﹣b）² ，由此推导出一个重要的定理．

(1)、此图可以推导出你学过的什么定理？请写出定理的内容；

(2)、图②为美国第二十任总统伽菲尔德创造的“无字证明”图形，请你利用图②推导（1）中的定理．

(3)、根据（1）中的定理，解决下面的问题：如图③，在一条东西走向河流的一侧有一村庄C ，河边原有两个取水点A ， B ，其中AB＝AC ，由于某种原因，由C到A的路现在已经不通，该村为方便村民取水决定在河边新建一个取水点H（A、H、B在同一条直线上），并新修一条路CH ，且CH⊥AB ．测得CH＝1.2千米，HB＝0.9千米，求新路CH比原路CA少多少千米？

查看试题解析
19. 勾股定理是人类最伟大的十个科学发现之一，西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三，股四，则弦五”的记载，我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”（如图①），后人称之为“赵爽弦图”，流传至今.如图①是用四个能够完全重合的直角三角形拼成的图形，其中直角边长分别为a，b，斜边长为c，用含a，b，c的代数式表示：

(1)、大正方形的面积为；小正方形的面积为；

(2)、四个直角三角形的面积和为，根据图中面积关系，可列出a，b，c之间的关系式为；

(3)、如图②，以直角三角形的三边为直径，分别向外部作半圆，则 $S_{1}$ ， $S_{2}$ ， $S_{3}$ 满足的关系是；

(4)、如图③直角三角形的两条直角边长分别为3、5，分别以直角三角形的三边为直径作半圆，则图中两个月形图案（阴影部分）的面积和为.

查看试题解析

苏科版数学八年级上册3.3勾股定理的简单应用专项练习

一、折枝问题

二、台风过境问题

三、面积问题

四、滑梯、拉绳问题

五、综合题