苏科版数学八年级上册3.3勾股定理的简单应用之蚂蚁爬行最短路径问题同步练习
试卷更新日期：2025-11-06 类型：同步测试
一、圆柱体
-
1. 如图，一圆柱体的底面圆周长为 ， 高为 ， 是上底的直径，一只蚂蚁从点A出发，沿着圆柱的侧面爬行到点C，则爬行的最短路程是（ ） ．
A、 B、 C、3 D、92. 如图所示，一根长为7 cm的吸管放在一个圆柱形杯中，测得杯的内部底面直径为3c m，高为4 cm，则吸管露在杯外面的最短长度为 cm.
3. 如图，一个圆柱的高为12cm，底面圆的周长为18cm.在圆柱下底面的点A 处有一只蚂蚁，它想吃到上底面上与点A 相对的点B处的食物，那么它沿圆柱侧面爬行的最短路程是多少?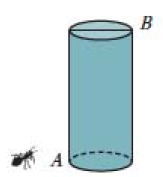
二、长方体
-
4. 如图，长方体的长为 ， 宽为 ， 高为 ， 点离点为 ， 一只蚂蚁如果要沿着长方体的表面从点爬到点去吃一滴蜜糖，需要爬行的最短距离是（ ）
A、 B、 C、 D、5. 如图， 一个长方体形盒子的长为15cm， 宽为10cm， 高为20cm， 点B到点C的距离是5cm.一只蚂蚁沿盒的外表面从点A处爬到点B处，那么它爬行的最短路程是多少?
6. 如图所示是长方体透明玻璃鱼缸，假设其长 AD = 80 cm，高 AB =60 cm，水深AE=40 cm.在水面上紧贴内壁G处有一块面包屑，G在水面线EF上，且EG=60cm，一只小虫想从鱼缸外的A 点沿鱼缸壁爬进鱼缸内的G处吃面包屑，则小虫爬行的最短路线长为cm.
7. 如图，三级台阶的每一级的长、宽、高分别为 ． 点A和B是这个台阶上两个相对的端点，点A处有一只蚂蚁，想到点B处去吃可口的食物，则蚂蚁沿着台阶面爬行到点B的最短路程为（ ）dm．
A、12 B、10 C、17 D、25三、多圈缠绕（圆柱体）
-
8. 农民麦子大丰收，小彬用打印机制作了一个底面周长为 ， 高为的圆柱粮仓模型（如图所示）．现要在此模型的侧面贴彩色装饰带，使装饰带从柱底沿圆柱表面均匀地缠绕2圈到达柱顶正上方（从点到点为的中点），则装饰带的长度最短为（ ）
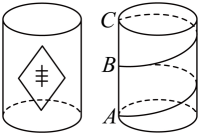A、 B、 C、 D、9. 国庆节期间，重庆南开中学用彩灯带装饰了艺术楼大厅的所有圆柱形柱子．为了美观，每根柱子的彩灯带需要从月点沿柱子表面缠绕两周到其正上方的3点，如图所示．若每根柱子的底面周长均为2米，高均为3米，则每根柱子所用彩灯带的最短长度为（ ）
A、米 B、米 C、米 D、5米10. 临汾是帝尧之都，有着尧都之称．尧都华表柱身祥云腾龙，顶蹲冲天吼，底座浮雕长城和黄河壶口瀑布，是中华民族历史悠久、文化灿烂的标志．如图，在底面周长约为6米且带有层层回环不断的云朵石柱上，有一条雕龙从柱底沿立柱表面均匀地盘绕2圈到达柱顶正上方（从点A到点 ， 为的中点），每根华表刻有雕龙的部分的柱身高约16米，则雕刻在石柱上的巨龙至少为 ．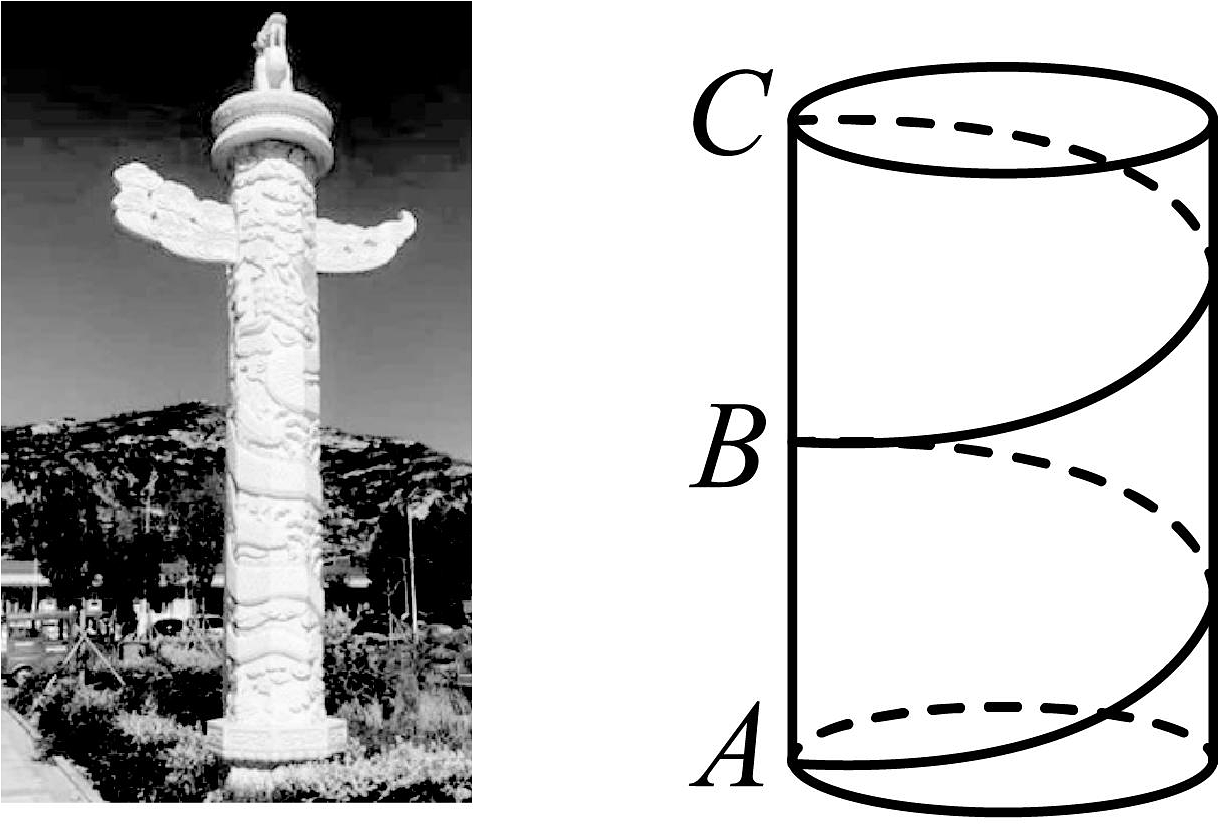
四、多圈缠绕（长方体）
-
11. 如图，长方体的底面边长分别为2cm和3cm，高为5cm．若一只蚂蚁从P点开始经过四个侧面爬行一圈到达Q点，则蚂蚁爬行的最短路径长为cm．
12. 解决下列几个问题，并说明它们与本节课问题的区别与联系.(1)、如图，圆柱的高为13cm，底面周长为10cm，在圆柱下底面的点A处有一只蚂蚁，它想吃到离上底面1cm的点B处的食物，那么它沿圆柱侧面爬行的最短路程是多少?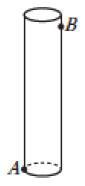
(2)、如图， 一个长方体形盒子的长、宽、高分别为8cm， 8cm，12cm，一只蚂蚁想从盒底的点 A 处沿盒的外表面爬到盒顶的点 B处，你能帮蚂蚁设计一条最短的路线吗?蚂蚁爬行的最短路程是多少?
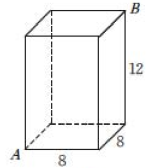(3)、为了营造节日气氛，学校准备在大厅圆柱上缠绕彩带.已知大厅圆柱的高为6m，底面周长为2m.如果希望彩带从圆柱底端绕圆柱4圈后正好到达顶端，那么至少需要彩带多少米?五、解答题
六、实践探究题
-
13. （1）问题再现：学习二次根式时，老师给同学们提出了一个求代数式最小值的问题，如，“求代数式的最小值”．小强同学发现可看作两直角边分别为和2的直角三角形斜边长，可看作两直角边分别是和4的直角三角形的斜边长．于是构造出如图所示，将问题转化为求线段的长，进而求得的最小值是______．
（2）类比计算：已知均为正数，且 ． 求的最小值．
（3）迁移问题：已知平面直角坐标系中， ， ， ， 直接写出的最小值．
14. 综合与实践【问题情境】
数学综合与实践活动课上，老师提出如下问题：一个三级台阶，它每一级的长、宽、高分别为、、 ， 和是一个台阶两个相对的端点．
【探究实践】
老师让同学们探究：如图①，若点处有一只蚂蚁要到点去吃可口的食物，那么蚂蚁沿着台阶爬到点的最短路程是多少？
（1）同学们经过思考得到如下解题方法：如图②，将三级台阶展开成平面图形，连接 ， 经过计算得到长度即为最短路程，则 ；（直接写出答案）
【变式探究】
（2）如图③，一只圆柱体玻璃杯，若该玻璃杯的底面周长是厘米，高是厘米，一只蚂蚁从点出发沿着玻璃杯的侧面到点 ， 求该蚂蚁爬行的最短路程是多少厘米？
【拓展应用】
（3）如图④，若圆柱体玻璃杯的高厘米，底面周长为厘米，在杯内壁离杯底厘米的点处有一滴蜂蜜．此时，一只蚂蚁正好在外壁，离杯上沿厘米，且与蜂蜜相对的点处，则蚂蚁从外壁处到内壁处所爬行的最短路程是多少厘米？（杯壁厚度不计）
15. 【阅读材料】如图1，有一个圆柱，它的高为12 cm，底面周长为18 cm．在圆柱下底面的点A处有一只蚂蚁，它想吃到上底面与点A相对的点B处的食物，蚂蚁沿圆柱侧面爬行的最短路程是多少？
【方法探究】对于立体图形中求最短路程问题，应把立体图形展开成平面图形，再确定A ， B两点的位置，依据“两点之间线段最短”，结合勾股定理，解决相应的问题．如图2，在圆柱的侧面展开图中，点A ， B对应的位置如图所示，利用勾股定理即可求出蚂蚁爬行的最短路程AB的长．
【方法应用】
(1)、如图3，圆柱形玻璃容器的高为18 cm，底面周长为60 cm，在外侧距下底1 cm的点S处有一蜘蛛，与蜘蛛相对的圆柱形容器的上口外侧距开口处1 cm的点F处有一苍蝇，试求急于捕获苍蝇充饥的蜘蛛，所走的最短路线的长度．(2)、如图4，长方体的棱长 ， ， 假设昆虫甲从盒内顶点处开始以1 cm/s的速度在盒子的内部沿棱向下爬行，同时昆虫乙从盒内顶点A处以相同的速度在盒内壁的侧面上爬行，那么昆虫乙至少需要多长时间才能捕捉到昆虫甲？