人教版数学八年级上学期期中仿真模拟试卷六(范围:1-3章)
试卷更新日期:2025-11-05 类型:期中考试
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. 下列交通标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一个等腰三角形的两边长分别为和 , 则它的周长是( )A、 B、 C、 D、或3. 在中, , , 则的形状是( )A、钝角三角形 B、直角三角形 C、锐角三角形 D、等边三角形4. 如图, , , , 则( )
2. 一个等腰三角形的两边长分别为和 , 则它的周长是( )A、 B、 C、 D、或3. 在中, , , 则的形状是( )A、钝角三角形 B、直角三角形 C、锐角三角形 D、等边三角形4. 如图, , , , 则( ) A、 B、 C、 D、5. 如图,在中, , , 是边上的两点, , 平分 , 下列说法不正确的是( )
A、 B、 C、 D、5. 如图,在中, , , 是边上的两点, , 平分 , 下列说法不正确的是( ) A、是的中线 B、 C、是的角平分线 D、是的高6. 如图为个边长相等的正方形的组合图形,则( )
A、是的中线 B、 C、是的角平分线 D、是的高6. 如图为个边长相等的正方形的组合图形,则( ) A、 B、 C、 D、7. 两个完全一样的三角板如图摆放,它们的顶点重合于点M,则点M一定在( )
A、 B、 C、 D、7. 两个完全一样的三角板如图摆放,它们的顶点重合于点M,则点M一定在( ) A、的平分线上 B、边的高上 C、边的垂直平分线上 D、边的中线上8. 如图,在中,按以下步骤作图:
A、的平分线上 B、边的高上 C、边的垂直平分线上 D、边的中线上8. 如图,在中,按以下步骤作图:①分别以B,C为圆心,以大于的长为半径作弧,两弧相交于两点M,N;
②作直线交于点D,连接 .
若 , , 则的度数为( )
 A、 B、 C、 D、9. 若一个等腰三角形有一个角为110°,那么它的底角的度数为( )A、110° B、55° C、110°或35° D、35°10. 如图,在中 , , D,E是BC上两点,且 , 过点A作 , 垂足是A,过点C作 , 垂足是C,CF交AF于点F,连接EF.给出下列结论:①;②;③若 , , 则;④ . 其中正确结论的字号是( )
A、 B、 C、 D、9. 若一个等腰三角形有一个角为110°,那么它的底角的度数为( )A、110° B、55° C、110°或35° D、35°10. 如图,在中 , , D,E是BC上两点,且 , 过点A作 , 垂足是A,过点C作 , 垂足是C,CF交AF于点F,连接EF.给出下列结论:①;②;③若 , , 则;④ . 其中正确结论的字号是( ) A、①②③ B、②③④ C、①③④ D、①②④
A、①②③ B、②③④ C、①③④ D、①②④二、填空题:本大题共5小题,每小题3分,共15分.
-
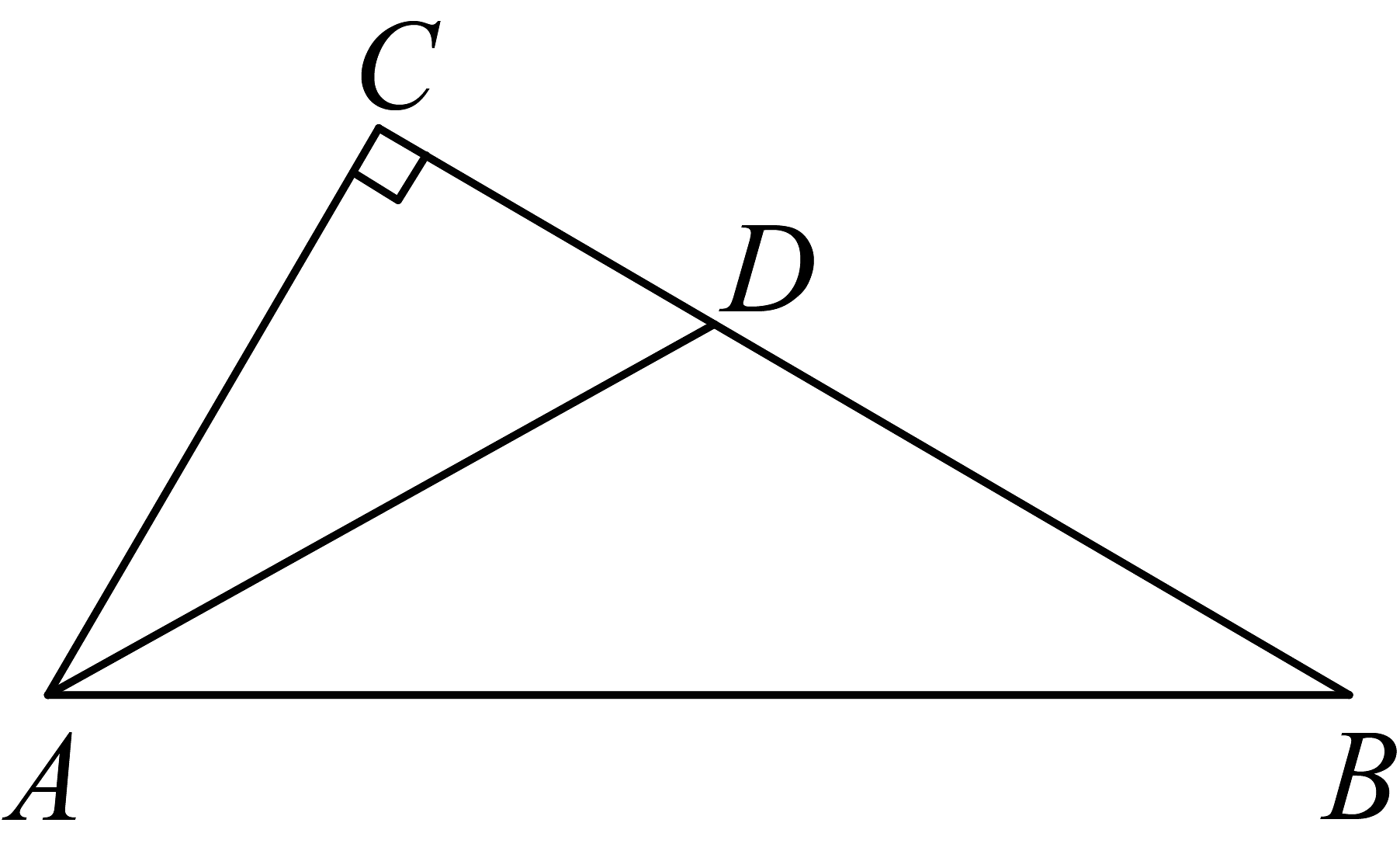
11. 如图,在中, , 平分 . 若 , , 则 .
 12. 如图, 已知 , 点B的对应点 E在线段上, , 则的大小是(度).
12. 如图, 已知 , 点B的对应点 E在线段上, , 则的大小是(度). 13. 如图,平分交于点为的中点,已知 , 则 .
13. 如图,平分交于点为的中点,已知 , 则 . 14. 如图,四边形中, , 平分 , , , 垂足为E,且 , 则的度数是 .
14. 如图,四边形中, , 平分 , , , 垂足为E,且 , 则的度数是 . 15. 如图,在中, , , , 平分 , 点F为的中点,E是上的动点,则和的最小值是 .
15. 如图,在中, , , , 平分 , 点F为的中点,E是上的动点,则和的最小值是 .
三、解答题:本大题共8小题,共75分.
-
16. 如图,在中, , 垂直平分 , 交于点 , 交于点 , 且是的中点,连接 .
 (1)、若 , 求的度数;(2)、若的长为 , 求的周长.17. 如图,点在上, , , , 说明的理由.
(1)、若 , 求的度数;(2)、若的长为 , 求的周长.17. 如图,点在上, , , , 说明的理由. 18. 如图,在正方形网格中点A,B,C均为格点,按要求作图(保留作图痕迹,不写作法):
18. 如图,在正方形网格中点A,B,C均为格点,按要求作图(保留作图痕迹,不写作法): (1)、作出关于直线l的对称图形;(2)、在直线l上找一点D,使最小.19. 如图,在中, , , 为中点,点在线段上,交于点 , .
(1)、作出关于直线l的对称图形;(2)、在直线l上找一点D,使最小.19. 如图,在中, , , 为中点,点在线段上,交于点 , . (1)、求度数;(2)、求的周长.20. 如图,AD=AC,AB=AE,∠DAB=∠CAE.
(1)、求度数;(2)、求的周长.20. 如图,AD=AC,AB=AE,∠DAB=∠CAE. (1)、△ADE与△ACB全等吗?说明理由;(2)、判断线段DF与CF的数量关系,并说明理由.21. 如图在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,求DF的长.
(1)、△ADE与△ACB全等吗?说明理由;(2)、判断线段DF与CF的数量关系,并说明理由.21. 如图在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,求DF的长.

