北师大版数学九年级第一学期期中检测C卷[范围：1-5章]

试卷更新日期：2025-11-03 类型：期中考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 用配方法解方程 $2 x^{2} - x - 1 = 0$ ，变形结果正确的是（）

A、 $(x - \frac{1}{2})^{2} = \frac{3}{4}$ B、 $(x - \frac{1}{4})^{2} = \frac{3}{4}$ C、 $(x - \frac{1}{4})^{2} = \frac{17}{16}$ D、 $(x - \frac{1}{4})^{2} = \frac{9}{16}$

查看试题解析
2. 如图，在△ABC中，点D、E分别在边AB、AC上，若DE∥BC， $\frac{A D}{D B} = \frac{2}{3}$ ，DE＝6cm，则BC的长为（）

A、9cm B、12cm C、15cm D、18cm

查看试题解析
3. 如图，四边形ABCD是矩形，对角线AC，BD相交于点O，点E，F分别在边AB，BC上，连接EF交对角线BD于点P．若P为EF的中点，∠ADB＝35°，则∠DPE＝（）

A、95° B、100° C、110° D、145°

查看试题解析
4. 我国“深蓝2号”大型智能深海养殖网箱的主体是一个正六棱柱，其示意图的主视图是（）

A、 B、 C、 D、

查看试题解析
5. 关于 $x$ 的一元一次方程 $(m + 1) x^{2} - 2 x + 1 = 0$ 有两个不相等的实数根，则 $m$ 的取值范围是（）

A、 $m < 0$ 且 $m \neq - 1$ B、 $m ⩾ 0$ C、 $m ⩽ 0$ 且 $m \neq - 1$ D、 $m < 0$

查看试题解析
6. 某钢铁厂一月份生产钢铁560吨，月平均增长率相同，第一季度共生产钢铁1860吨，若设月平均增长率为 $x$ ，那么可列出的方程是 $($ 　　 $)$

A、 $560 (1 + x)^{2} = 1860$ B、 $560 + 560 (1 + x) + 560 (1 + 2 x) = 1860$ C、 $560 + 560 (1 + x) + 560 (1 + x)^{2} = 1860$ D、 $560 + 560 (1 + 2 x)^{2} = 1860$

查看试题解析
7. 某商场开展购物抽奖促销活动，抽奖盒中装有三个小球，它们分别标有10元、20元、30元，一次性随机摸出两个小球，摸出的两球上金额的和为50元的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
8. 如图，在菱形ABCD中， $∠ B = 4 5^{°}, A B = 6$ ，点 $E$ 在边BC上，连接AE，将 $△ A B E$ 沿AE折叠，若点 $B$ 落在BC延长线上的点 $F$ 处，则CF的长为（）

A、2 B、 $6 - 3 \sqrt{2}$ C、 $2 \sqrt{2}$ D、 $6 \sqrt{2} - 6$

查看试题解析
9. 如图，在正方形 $A B C D$ 中，点 $E$ ， $F$ 分别在 $B C$ ， $C D$ 上，连接 $A E$ ， $A F$ ， $E F$ ， $∠ E A F = 45 °$ ．若 $∠ B A E = α$ ，则 $∠ F E C$ 一定等于（）

A、 $2 α$ B、 $90 ° - 2 α$ C、 $45 ° - α$ D、 $90 ° - α$

查看试题解析
10. 如图，将矩形 $A B C D$ 沿着 $G E$ 、 $E C$ 、 $G F$ 翻折，使得点 $A$ 、 $B$ 、 $D$ 恰好都落在点 $O$ 处，且点 $G$ 、 $O$ 、 $C$ 在同一条直线上，同时点 $E$ 、 $O$ 、 $F$ 在另一条直线上.小炜同学得出以下结论：
① $G F ∥ E C$ ；② $A B = \frac{4 \sqrt{3}}{5} A D$ ；③ $G E = \sqrt{6} D F$ ；④ $O C = 2 \sqrt{2} O F$ ；⑤ $△ C O F ∽ △ C E G$ .

其中正确的是（）

A、①②③ B、①③④ C、①④⑤ D、②③④

查看试题解析

二、填空题（每题3分，共18分）

11. 已知 $\frac{x}{2} = \frac{y}{3} = \frac{z}{4} \neq 0$ ，则 $\frac{x^{2} + x y}{y z} =$

查看试题解析
12. 关于x的一元二次方程2x²+4mx+m=0有两个不同的实数根x₁ ， x₂ ，且 $x_{1}^{2} + x_{2}^{2} = \frac{3}{16}$ ，则m= ．

查看试题解析
13. 如图，菱形 $A B C D$ 的边长为2， $∠ A B C = 60 °$ ，对角线 $A C$ 与 $B D$ 交于点 $O$ ， $E$ 为 $O B$ 中点， $F$ 为 $A D$ 中点，连接 $E F$ ，则 $E F$ 的长为．

查看试题解析
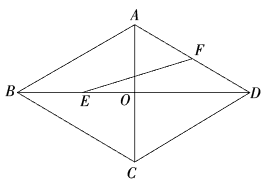14. 如图，在菱形ABCD中， $B C = 2$ ， $∠ C = 120 °$ ，Q为AB的中点，P为对角线BD上的任意一点，则 $A P + P Q$ 的最小值为.

查看试题解析
15. 如图，在矩形 $A B C D$ 中，点E ， F ， M分别在 $A B$ ， $D C$ ， $A D$ 边上， $B E = 2 C F, F M$ 分别交对角线 $B D$ 、线段 $D E$ 于点G ， H ，且 $H$ 是 $D E$ 的中点．若 $C F = 2, ∠ A B D = 30 °$ ，则 $H G$ 的长为．

查看试题解析
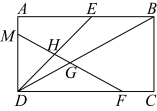16. 一个几何体的三视图如图所示，则该几何体的表面积为．

查看试题解析

三、解答题（共8题，共72分）

17.

(1)、用配方法解方程： $x^{2} - 2 x - 7 = 0$ ；

(2)、解方程： $3 x^{2} = 2 - 5 x$ ．

查看试题解析
18. 内江，东汉建县，古称汉安，是一座依江而生、因水得名的城市．“成渝之心、大千故里、甜蜜之城”是新时代内江的三张靓丽名片，也是“心里甜”的由来，为弘扬内江传统文化，我市将举办中小学生“知内江、爱内江、兴内江”知识竞赛活动．某校举办选拔赛后，随机抽取了部分学生的成绩，成绩按百分制分为A、B、C、D四个等级，并绘制了如下两幅不完整的统计图表．
等级
成绩 $(x)$
人数
$A$
$95 < x \leq 100$
$m$
$B$
$85 < x \leq 95$
24
$C$
$75 < x \leq 85$
14
$D$
$x \leq 75$
10
根据统计图表中的信息解答下列问题：

(1)、表中 $m =$ ；扇形统计图中，表示成绩等级为D的扇形圆心角为度．

(2)、若全校有3000人参加了此次选拔赛，其中成绩等级为A的学生大约有多少人？

(3)、现从成绩等级为A的甲、乙、丙、丁4人中随机选出2人参加市级比赛，请通过列表或画树状图的方法求出甲、乙两人同时被选中的概率．

查看试题解析
19. 如图，在矩形 $A B C D$ 中，点 $E$ 是 $A D$ 的中点，将矩形 $A B C D$ 沿 $B E$ 所在的直线折叠， $C ， D$ 的对应点分别为 $C^{'}$ ， $D^{'}$ ，连接 $A D^{'}$ 交 $B C^{'}$ 于点 $F$ ．

(1)、若 $∠ D E D^{'} = 70 °$ ，求 $∠ D A D^{'}$ 的度数；

(2)、连接EF ，试判断四边形 $C^{'} D^{'} E F$ 的形状，并说明理由．

查看试题解析

20. 根据以下素材，探索完成任务．

素材1	随着数字技术、新能源、新材料等不断突破，我国制造业发展迎来重大机遇．某工厂一车间借助智能化，对某款车型的零部件进行一体化加工，生产效率提升，该零件4月份生产100个，6月份生产144个．
素材2	该厂生产的零件成本为30元/个，销售一段时间后发现，当零件售价为40元/个时，月销售量为600个，若在此基础上售价每上涨1元，则月销售量将减少10个．
问题解决
任务1	求该车间4月份到6月份生产数量的平均增长率；
任务2	为使月销售利润达到10000元，而且尽可能让车企得到实惠，则该零件的实际售价应定为多少元？

查看试题解析

21. 课本再现

思考

我们知道，菱形的对角线互相垂直．反过来，对角线互相垂直的平行四边形是菱形吗？

可以发现并证明菱形的一个判定定理；

对角线互相垂直的平行四边形是菱形．

(1)、定理证明：为了证明该定理，小明同学画出了图形（如图1），并写出了“已知”和“求证”，请你完成证明过程．

已知：在 $▱ A B C D$ 中，对角线 $B D ⊥ A C$ ，垂足为 $O$ ．

求证： $▱ A B C D$ 是菱形．

(2)、知识应用：如图

2

，在

▱ A B C D

中，对角线

A C

和

B D

相交于点

O

，

A D = 5 ， A C = 8 ， B D = 6

．

①求证： $▱ A B C D$ 是菱形；

②延长 $B C$ 至点 $E$ ，连接 $O E$ 交 $C D$ 于点 $F$ ，若 $∠ E = \frac{1}{2} ∠ A C D$ ，求 $\frac{O F}{E F}$ 的值．

查看试题解析

22. 如图，在平行四边形ABCD中，连接对角线AC ，延长AB至点E ，使 $B E = A B$ ，连接DE ，分别交BC ， AC交于点F ， G ．

(1)、求证： BF=CF ；

(2)、若 $B C = 6$ ， $D G = 4$ ，求FG的长．

查看试题解析
23. 将一副直角三角板 $D O E$ 与 $A O C$ 叠放在一起，如图1， $∠ O = 90 °$ ， $∠ A = 30 °$ ， $∠ E = 45 °$ ， $O D > O C$ ．在两三角板所在平面内，将三角板 $D O E$ 绕点O顺时针方向旋转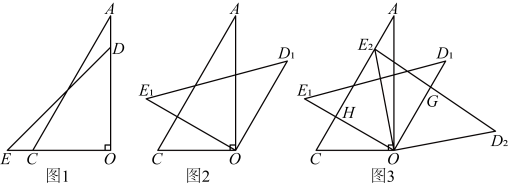 $α$ （ $0 ° < α < 90 °$ ）度到 $D_{1} O E_{1}$ 位置，使 $O D_{1} ∥ A C$ ，如图2．

(1)、求 $α$ 的值；

(2)、如图3，继续将三角板 $D O E$ 绕点O顺时针方向旋转，使点E落在 $A C$ 边上点 $E_{2}$ 处，点D落在点 $D_{2}$ 处．设 $E_{2} D_{2}$ 交 $O D_{1}$ 于点G， $O E_{1}$ 交 $A C$ 于点H，若点G是 $E_{2} D_{2}$ 的中点，试判断四边形 $O H E_{2} G$ 的形状，并说明理由．

查看试题解析
24. 问题情境：小红同学在学习了正方形的知识后，进一步进行以下探究活动：在正方形 $A B C D$ 的边 $B C$ 上任意取一点G，以 $B G$ 为边长向外作正方形 $B E F G$ ，将正方形 $B E F G$ 绕点B顺时针旋转．

(1)、特例感知：
当 $B G$ 在 $B C$ 上时，连接 $D F ， A C$ 相交于点P，小红发现点P恰为 $D F$ 的中点，如图①．针对小红发现的结论，请给出证明；

(2)、小红继续连接 $E G$ ，并延长与 $D F$ 相交，发现交点恰好也是 $D F$ 中点P，如图②，根据小红发现的结论，请判断 $△ A P E$ 的形状，并说明理由；

(3)、规律探究：
如图③，将正方形 $B E F G$ 绕点B顺时针旋转 $α$ ，连接 $D F$ ，点P是 $D F$ 中点，连接 $A P$ ， $E P$ ， $A E$ ， $△ A P E$ 的形状是否发生改变？请说明理由．

查看试题解析

等级	成绩 $(x)$	人数
$A$	$95 < x \leq 100$	$m$
$B$	$85 < x \leq 95$	24
$C$	$75 < x \leq 85$	14
$D$	$x \leq 75$	10