北师大版数学九年级第一学期期中检测B卷[范围:1-5章]
试卷更新日期:2025-11-02 类型:期中考试
一、选择题(每题3分,共30分)
-
1. 用配方法解一元二次方程 , 配方后得到的方程是( )A、 B、 C、 D、2. 一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根3. 如图,菱形的面积为10,点E , F , G , H分别为 , , , 的中点,则四边形的面积为( )
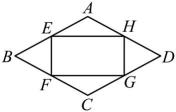 A、 B、5 C、4 D、84. 如图,矩形的对角线相交于点 , 下列结论一定正确的是( )
A、 B、5 C、4 D、84. 如图,矩形的对角线相交于点 , 下列结论一定正确的是( ) A、平分 B、 C、 D、5. 如图,有一张矩形纸片先对折矩形 , 使与重合,得到折痕 , 把纸片展平再一次折叠纸片,使点落在上,并使折痕经过点 , 得到折痕 , 同时得到线段 , 观察所得的线段,若 , 则( )
A、平分 B、 C、 D、5. 如图,有一张矩形纸片先对折矩形 , 使与重合,得到折痕 , 把纸片展平再一次折叠纸片,使点落在上,并使折痕经过点 , 得到折痕 , 同时得到线段 , 观察所得的线段,若 , 则( ) A、 B、 C、 D、6. 如图,在长为 , 宽为的矩形地面的四周种植花卉,中间种植草坪.如果要求花卉带的宽度相同,且草坪的面积为总面积的 , 那么花卉带的宽度应为多少米?设花卉带的宽度为 , 则可列方程为( )
A、 B、 C、 D、6. 如图,在长为 , 宽为的矩形地面的四周种植花卉,中间种植草坪.如果要求花卉带的宽度相同,且草坪的面积为总面积的 , 那么花卉带的宽度应为多少米?设花卉带的宽度为 , 则可列方程为( )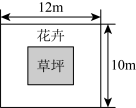 A、 B、 C、 D、7. 如图,小莹对三个相连的方格进行涂色.在给每个方格涂色时,均从红、蓝两种颜色中随机选取一种,那么相邻两个方格所涂颜色不同的概率是( )
A、 B、 C、 D、7. 如图,小莹对三个相连的方格进行涂色.在给每个方格涂色时,均从红、蓝两种颜色中随机选取一种,那么相邻两个方格所涂颜色不同的概率是( ) A、 B、 C、 D、8. 如图,一块面积为60cm2的三角形硬纸板(记为△ABC)平行于投影面时,在点光源O的照射下形成的投影是△A1B1C1 , 若OB:BB1=2:3,则△A1B1C1的面积是( )
A、 B、 C、 D、8. 如图,一块面积为60cm2的三角形硬纸板(记为△ABC)平行于投影面时,在点光源O的照射下形成的投影是△A1B1C1 , 若OB:BB1=2:3,则△A1B1C1的面积是( ) A、90cm2 B、135cm2 C、150cm2 D、375cm29. 如图是一个几何体的三视图(图中尺寸单位:cm),则这个几何体的底面圆的周长为( )
A、90cm2 B、135cm2 C、150cm2 D、375cm29. 如图是一个几何体的三视图(图中尺寸单位:cm),则这个几何体的底面圆的周长为( ) A、6πcm B、9πcm C、12πcm D、16πcm
A、6πcm B、9πcm C、12πcm D、16πcm二、填空题(每题3分,共18分)
-
10. 若一元二次方程的两根为 , 则的值为 .11. 如图,菱形ABCD的边长为2,∠ABC=60°,对角线AC、BD相交于点M . 过点D作AC的平行线交BC的延长线于点N , 连接MN . 则MN的长为 .
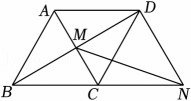 12. 如图,在梯形ABCD中, , 对角线AC和BD交于点O , 若 , 则 .
12. 如图,在梯形ABCD中, , 对角线AC和BD交于点O , 若 , 则 . 13. 如图,在中,点D , E分别在边上.添加一个条件使 , 则这个条件可以是 . (写出一种情况即可)
13. 如图,在中,点D , E分别在边上.添加一个条件使 , 则这个条件可以是 . (写出一种情况即可) 14. 如图,在▱ABCD中,对角线AC与BD相交于点O.小乐同学欲添加两个条件使得四边形ABCD是正方形,现有三个条件可供选择:①AC⊥BD;②AC=BD;③∠ADC=90°.则正确的组合是 (只需填一种组合即可).
14. 如图,在▱ABCD中,对角线AC与BD相交于点O.小乐同学欲添加两个条件使得四边形ABCD是正方形,现有三个条件可供选择:①AC⊥BD;②AC=BD;③∠ADC=90°.则正确的组合是 (只需填一种组合即可).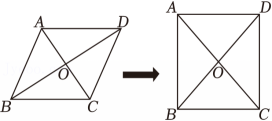 15. 如图,菱形中, , 面积为60,对角线AC与BD相交于点O,过点A作 , 交边于点E,连接 , 则 .
15. 如图,菱形中, , 面积为60,对角线AC与BD相交于点O,过点A作 , 交边于点E,连接 , 则 .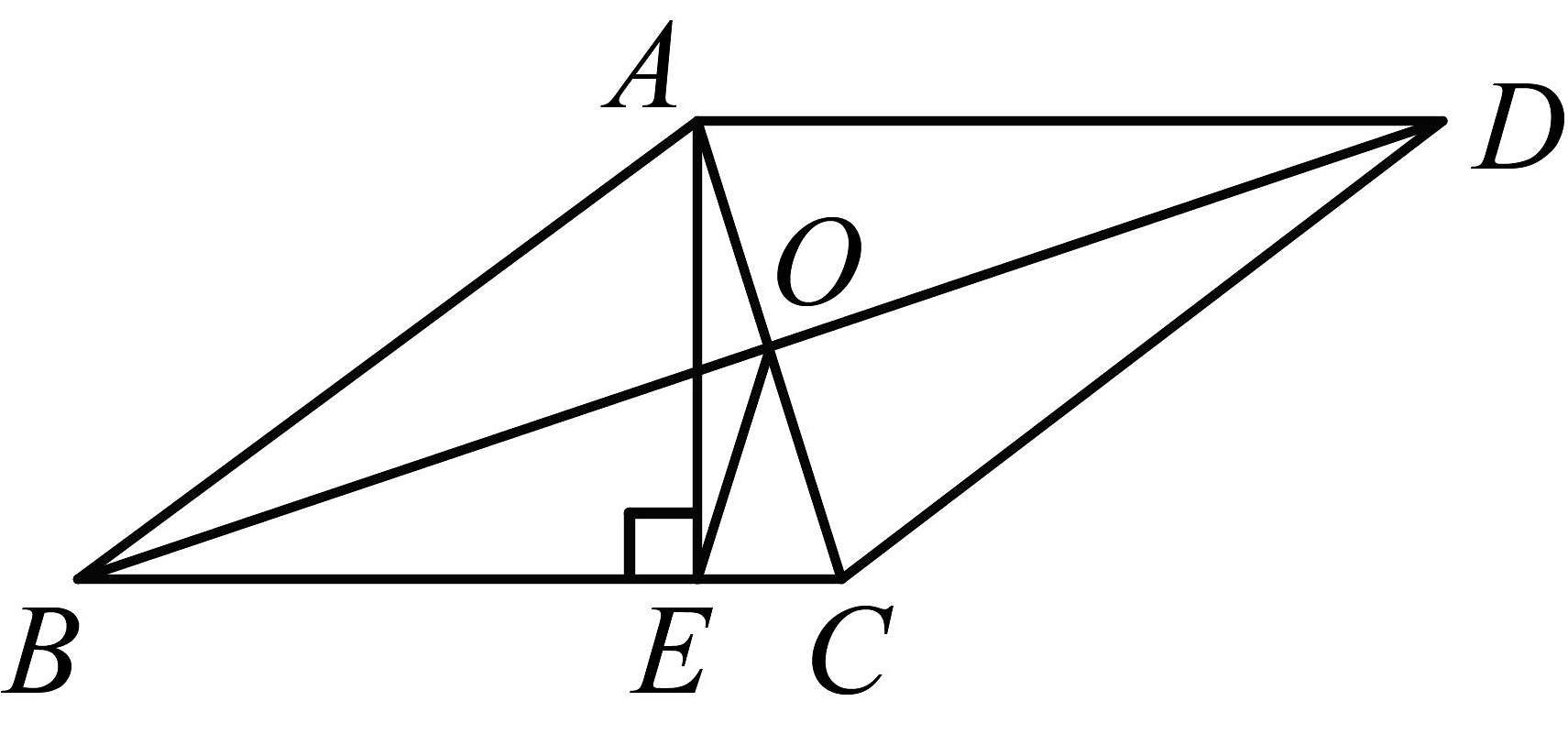
三、解答题(共8题,共72分)
-
16. 解下列方程(1)、(配方法);(2)、2x2-7x+6=0(公式法).17. 已知关于的一元二次方程有两个实数根 , .(1)、求的取值范围;(2)、若 , 满足 , 求的值.18. 一只不透明的袋子中装有标号分别为1,2,3,4的4个球,这些球除标号外都相同.(1)、将球搅匀,从中任意摸出1个球,摸到标号为2的球的概率是 ;(2)、将球搅匀,从中任意摸出1个球,记录标号后不放回,再从袋子中任意摸出1个球,记录标号.求两次摸到的球标号均小于3的概率.(请用“画树状图”或“列表”等方法写出分析过程)19. 如图,在△ABC中,点分别是边的中点,与相交于点 , 连接 . 证明:
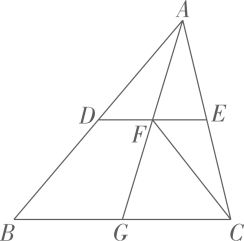 (1)、;(2)、△ADF≌△CFE .20. 如图.在四边形中, , 对角线与相交于点 . 点B , 点D关于所在直线对称.
(1)、;(2)、△ADF≌△CFE .20. 如图.在四边形中, , 对角线与相交于点 . 点B , 点D关于所在直线对称.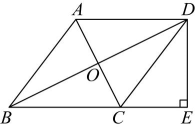 (1)、求证:四边形是菱形;(2)、过点D作的垂线交延长线于点E . 若 , , 求线段长.21. “我运动,我健康,我快乐!”随着人们对身心健康的关注度越来越高.某市参加健身运动的人数逐年增多,从2021年的32万人增加到2023年的50万人.(1)、求该市参加健身运动人数的年均增长率;(2)、为支持市民的健身运动,市政府决定从公司购买某种套装健身器材.该公司规定:若购买不超过100套,每套售价1600元;若超过100套,每增加10套,售价每套可降低40元.但最低售价不得少于1000元.已知市政府向该公司支付货款24万元,求购买的这种健身器材的套数.22. 在四边形ABCD中,对角线AC、BD相交于点O,AB=2,AD=1.
(1)、求证:四边形是菱形;(2)、过点D作的垂线交延长线于点E . 若 , , 求线段长.21. “我运动,我健康,我快乐!”随着人们对身心健康的关注度越来越高.某市参加健身运动的人数逐年增多,从2021年的32万人增加到2023年的50万人.(1)、求该市参加健身运动人数的年均增长率;(2)、为支持市民的健身运动,市政府决定从公司购买某种套装健身器材.该公司规定:若购买不超过100套,每套售价1600元;若超过100套,每增加10套,售价每套可降低40元.但最低售价不得少于1000元.已知市政府向该公司支付货款24万元,求购买的这种健身器材的套数.22. 在四边形ABCD中,对角线AC、BD相交于点O,AB=2,AD=1. (1)、若△ABD是等腰三角形,则BD=(2)、已知OB=OD,AC=BD.
(1)、若△ABD是等腰三角形,则BD=(2)、已知OB=OD,AC=BD.①若OA=OC,判断四边形ABCD是怎样的特殊四边形,并说明理由;
②如图,在△ACD中,CD2=AD2+AC2 , 求AC的长.
23. 已知点O是正方形ABCD的中心,点P , E分别是对角线AC , 边BC上的动点(均不与端点重合),作射线PE . (1)、将射线PE绕点P逆时针旋转90°,交边CD于点F.
(1)、将射线PE绕点P逆时针旋转90°,交边CD于点F.①如图1,当点P与点O重合时,求证:PE=PF;
②如图2,当时,请判断是否为定值.如果是,请求出该定值;如果不是,请说明理由;
(2)、如图3,连接BP,当∠BPE=45°时,将射线PE绕点P顺时针旋转90°,交边AB于点F.若 , PE=a,求四边形PEBF的面积(用含a,k的式子表示).