平面直角坐标系中的轴对称问题——浙教版八年级上册培优训练

试卷更新日期：2025-11-02 类型：复习试卷

进入出卷网下载

一、选择题

1. 点 $P (2 ， 3)$ 关于y轴对称的点的坐标是（）

A、 $(2 ， 3)$ B、 $(- 2 ， 3)$ C、 $(2, - 3)$ D、 $(- 2 ， - 3)$

查看试题解析
2. 已知点A(4，-3)和点B是坐标平面内的两个点，且它们关于直线x=2对称，则平面内点B的坐标为( )

A、(0，-3) B、(4，-9) C、(4，0 ) D、(-10，3)

查看试题解析
3. 在平面直角坐标系中，点 $A (m, 2)$ 与点 $B (3, n)$ 关于 $y$ 轴对称，则 $m + n =$ （）

A、 $- 5$ B、 $- 1$ C、1 D、5

查看试题解析
4. 如图，将点 $P (- 1, 2)$ 关于第一、三象限的角平分线对称，得到点 $P'$ ，则点 $P'$ 的坐标为（）

A、 $(2, 1)$ B、 $(2, - 1)$ C、 $(1, - 2)$ D、 $(- 1, - 2)$

查看试题解析
5. 如图，平面直角坐标系 $x O y$ 中，点 $A$ 在第一象限， $B (2, 0)$ ， $∠ A O B = 60 °$ ， $∠ A B O = 90 °$ ．在 $x$ 轴上取一点 $P (m, 0)$ ，过点 $P$ 作直线 $l$ 垂直于直线 $O A$ ，将 $O B$ 关于直线 $l$ 的对称图形记为 $O^{'} B^{'}$ ，当 $O^{'} B^{'}$ 和过 $A$ 点且平行于 $x$ 轴的直线有交点时， $m$ 的取值范围为（）

A、 $m \geq 4$ B、 $m \leq 6$ C、 $4 < m < 6$ D、 $4 \leq m \leq 6$

查看试题解析
6. 在平面直角坐标系中，对 $Δ A B C$ 进行循环往复的轴对称变换，若原来点 $A$ 的坐标是 $(\sqrt{3} ， \sqrt{2})$ ，则经过第2019次变换后所得的点 $A$ 的坐标是（）

A、 $(- \sqrt{3} ， \sqrt{2})$ B、 $(- \sqrt{3} ， - \sqrt{2})$ C、 $(\sqrt{3} ， - \sqrt{2})$ D、 $(\sqrt{3} ， \sqrt{2})$

查看试题解析

二、填空题

7. 点 $P (- 2, 3)$ 关于x轴的对称点的坐标是．

查看试题解析
8. 点 $(2 + a ， 3)$ 关于y轴对称的点的坐标是 $(- 4 ， 6 - b)$ ，则 $a b =$ ．

查看试题解析
9. 若点 $M (2 m - 1, 1 + m)$ 关于 $y$ 轴的对称点 $M^{'}$ 在第二象限，则 $m$ 的取值范围是．

查看试题解析
10. 点Q的横坐标为一元一次方程3x+7=32-2x的解，纵坐标为a+b的值，其中a，b满足二元一次方程组 ${\begin{matrix} 2 a - b = 4, \\ - a + 2 b = - 8, \end{matrix}$ 则点 Q 关于y轴对称的点Q^'的坐标为.

查看试题解析
11. 如图，在平面直角坐标系 $x O y$ 中，已知 $A (5, 0)$ ， $B (0, 4)$ ，过点B作y轴的垂线l，P为直线l上一动点，连接 $P O$ ， $P A$ ，则 $P O + P A$ 的最小值为．

查看试题解析
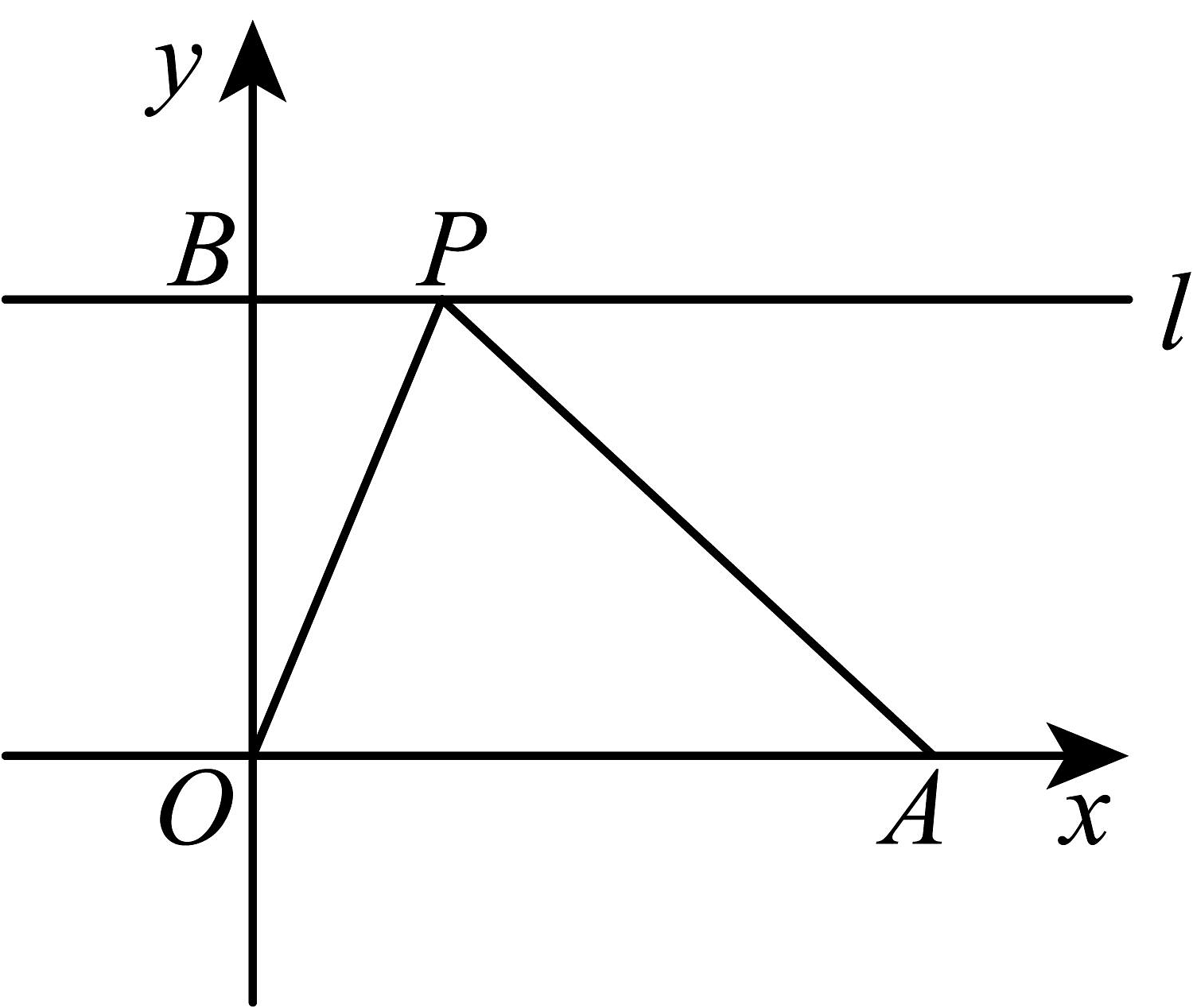12. 如图，在平面直角坐标系中，直线 $l$ 经过原点和一三象限，点 $A$ 为 $x$ 轴正半轴上一点，点 $B$ 位于第一象限内且在直线 $l$ 上， $O B = 2$ ， $∠ A O B = 30 °$ ，过点 $B$ 作直线 $a$ 垂直于 $x$ 轴，点 $C$ ， $D$ 在直线 $a$ 上(点 $D$ 在点 $C$ 上方)，且 $C D = 1$ ，若线段 $C D$ 关于直线 $l$ 对称的线段 $E F$ 与坐标轴有交点，则点 $C$ 的纵坐标 $m$ 的取值范围是．

查看试题解析
13. 在平面直角坐标系 $x O y$ 中，已知点 $P (a, b)$ 对于点 $P$ 和正实数 $m$ 给出如下定义：若 $|a| \leq |b|$ ，点 $P$ 向右平移 $m$ 个单位，再关于 $x$ 轴对称，得到点 $P^{'}$ ；若 $|a| > |b|$ ，点 $P$ 向上平移 $m$ 个单位，再关于 $y$ 轴对称，得到点 $P^{'}$ ，称点 $P^{'}$ 为点 $P$ 的“ $m$ -变换”点，点 $P$ 为点 $P^{'}$ 的“反 $m$ -变换”点．例如，已知 $A (5, 2)$ ， $B (- 2, - 3)$ ，当 $m = 2$ 时，点 $A$ 的“2-变换”点为 $A^{'} (- 5, 4)$ ，点 $B$ 的“2-变换”点为 $B^{'} (0, 3)$ ．

(1)、当 $m = 3$ 时，
①已知点 $P (- 1, 0)$ ，则点 $P$ 的“3-变换”点为_______；
②点 $M^{'} (1, 3)$ 的“反3-变换”点 $M$ 坐标为_______，点 $N^{'} (- 2, 3)$ 的“反3-变换”点 $N$ 坐标为_______；

(2)、已知 $C (8, 0), D (8, 6), E (0, 6)$ ，记长方形 $O C D E$ 上及内部所有点的“反 $m$ -变换”点组成的图形面积为 $S$ ．
①当 $m = 4$ 时， $S =$ _______；
②当 $0 < m < 6$ 时， $S =$ _______．（用含 $m$ 的式子表示）

查看试题解析
14. 如图已知点 $A (- 3, 0)$ ， $B (0, - 4)$ ， $E (6, 0)$ ，点 $A, C$ 关于 $y$ 轴对称，点 $D, B$ 关于 $x$ 轴对称， $△ P E F$ 是等腰直角三角形， $∠ P E F = 90 °$ ，点 $P$ 在四边形 $A B C D$ 边上从点A出发，以每秒5个单位长度沿 $A \to B \to C \to D \to A$ 方向运动，则第2025秒时，点 $F$ 的坐标为．

查看试题解析

三、解答题

15. 如图，在平面直角坐标系中， $△ A B C$ 各顶点的坐标分别为A(0，-1)，B(1，-3)，C(3，-2)，过点(-1，0)作x轴的垂线l.

(1)、作出 $△ A B C$ 关于x轴对称的 $△ A_{1} B_{1} C_{1},$ ，并写出 $△ A_{1} B_{1} C_{1}$ 各顶点的坐标；

(2)、作出 $△ A_{1} B_{1} C_{1}$ 关于直线l对称的 $△ A_{2} B_{2} C_{2},$ 并写出 $△ A_{2} B_{2} C_{2}$ 各顶点的坐标.

查看试题解析
16. 在平面直角坐标系中，将点 $P (x, y)$ 关于y轴的对称点记作点 $P_{1}$ ，再将点 $P_{1}$ 关于直线y=m的对称点记作点 $P_{2}$ ，则点 $P_{2}$ 为点 $P (x, y)$ 关于y轴和直线y=m的“DT对称点”．例如：点P（3，1）关于y轴和直线y=3的“DT对称点”为点 $P_{2} (- 3, 5)$ ．

(1)、点A（3，4）关于y轴和直线y=1的“DT对称点” $A_{2}$ 的坐标；

(2)、点 $B (3 m + n, m - n)$ 关于y轴和直线y=m的“DT对称点” $B_{2}$ 的坐标是 $(- 9, 5)$ ，求m和n的值；

(3)、若点 $C (6 x - 5, 2 x + 1)$ 关于y轴和直线y=m的“DT对称点” $C_{2}$ 在第二象限，且满足条件的x的整数解有且只有一个，求m的取值范围．

查看试题解析
17. 在平面直角坐标系中，经过点 $M (m, 0)$ 且平行于 $y$ 轴的直线记作直线 $x = m$ ．将点 $P (x, y)$ 关于 $x$ 轴的对称点记作点 $P_{1}$ ，再将点 $P_{1}$ 关于直线 $x = m$ 的对称点记作点 $P_{2}$ ，则称点 $P_{2}$ 为点 $P (x ， y)$ 关于 $x$ 轴和直线 $x = m$ 的“西雅对称点”．例如：点 $P (5, 1)$ 关于 $x$ 轴和直线 $x = 3$ 的“西雅对称点”为点 $P_{2} (1, - 1)$ ．

(1)、点 $A (4, 3)$ 关于 $x$ 轴和直线 $x = 1$ 的“西雅对称点” $A_{2}$ 的坐标是___________；

(2)、点 $B (3 m + n, m - n)$ 关于 $x$ 轴和直线 $x = m$ 的“西雅对称点” $B_{2}$ 的坐标是 $(- 9, 5)$ ，求 $m$ 和 $n$ 的值；

(3)、若点 $C (y + 1, 3 y - 12)$ 关于 $x$ 轴和直线 $x = m$ 的“西雅对称点” $C_{2}$ 在第二象限，且得到关于 $y$ 的取值范围内的所有整数解之和为6，求 $m$ 的取值范围．

查看试题解析
18. 如图1，在平面直角坐标系中，点A的坐标为（0，8），点B在第一象限，△OAB为等边三角形．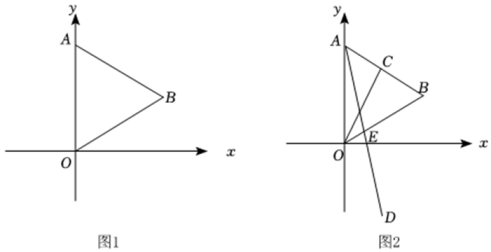

(1)、直接写出点B的纵坐标；

(2)、如图2，OC⊥AB于点C，点C关于x轴的对称点为点D，则点D的纵坐标为；

(3)、OC⊥AB于点C，点C关于x轴的对称点为点D，连接AD交OB于E，求OE的长．

查看试题解析
19. 如图，在平面直角坐标系 $x O y$ 中，直线l经过点 $M (4, 0)$ ，且平行于y轴．给出如下定义：点 $P (x, y)$ 先关于y轴对称得点 $P_{1}$ ，再将点 $P_{1}$ 关于直线l对称得点 $P^{'}$ ，则称点 $P^{'}$ 是点P关于y轴和直线l的二次反射点．

(1)、已知 $A (- 5, 0)$ ， $B (\frac{1}{2}, 1)$ ， $C (3, - 1)$ ，则它们关于y轴和直线l的二次反射点 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 的坐标分别是 $A^{'}$ ______， $B^{'}$ ______， $C^{'}$ ______；

(2)、若点D的坐标是 $(a, 0)$ ，点D关于y轴和直线l的二次反射点是点 $D^{'}$ ，求线段 $D D^{'}$ 的长；

(3)、已知点 $P (a, 1)$ ， $Q (a + 1, 1)$ ， $E (5 - a, 0)$ ， $F (7 - a, 0)$ ，以线段 $E F$ 为边在x轴上方作正方形 $E F G H$ ，若点P，Q关于y轴和直线l的二次反射点分别为 $P^{'}$ ， $Q^{'}$ ，且线段 $P^{'} Q^{'}$ 与正方形 $E F G H$ 的边有公共点，直接写出a的取值范围．

查看试题解析
20. 如图，等腰直角 $△ A B C$ 中， $B C = A C$ ， $∠ A C B = 90 °$ ，现将该三角形放置在平面直角坐标系中，点B坐标为 $(0, 3)$ ，点C坐标为 $(9, 0)$ ．过点A作 $A D ⊥ x$ 轴，垂足为D．

(1)、求OD的长及点A的坐标；

(2)、取AB中点E，连接OE、DE，请你判定OE与DE的关系，并证明你的结论；

(3)、连接OA，已知 $O A = 15$ ，试探究在x轴上是否存在点Q，使 $△ O A Q$ 是以OA为腰的等腰三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．

查看试题解析