平面直角坐标系中图形性质-浙教版数学八年级上册培优训练

试卷更新日期：2025-11-02 类型：复习试卷

进入出卷网下载

一、选择题

1. 如图，长方形纸片 $A B C D$ 的边 $B C$ 在 $x$ 轴上，且过原点，连结 $O D .$ 将纸片沿 $O D$ 折叠，使点 $C$ 恰好落在边 $A B$ 上的点 $C'$ 处 $.$ 若 $C' (- 4,3)$ ，则点 $D$ 的纵坐标为（）

A、 $9$ B、 $12$ C、 $14$ D、 $15$

查看试题解析
2. 如图，在平面直角坐标系中， $A B = A C = 13$ ，点 $B, C$ 的坐标分别为 $(7,2), (7,12)$ ，则点 $A$ 的坐标为（）

A、 $(- 5,5)$
B、 $(- 5,7)$ C、 $(- 7,5)$
D、 $(- 7,7)$

查看试题解析
3. 如图，在平面直角坐标系中，点A的坐标是 $(- 5, 0)$ ，点B的坐标是 $(0, 12)$ ，点M是 $O B$ 上一点，将 $△ A B M$ 沿 $A M$ 折叠，点B恰好落在x轴上的点 $B^{'}$ 处，则点M的坐标为（）

A、 $(\frac{10}{3}, 0)$ B、 $(0, \frac{10}{3})$ C、 $(\frac{13}{2}, 0)$ D、 $(0, \frac{13}{2})$

查看试题解析
4. 如图，△ABC中，∠A=67.5°，BC=4，BE⊥CA于E，CF⊥AB于 F，D是BC的中点.以F为原点，FD所在直线为x轴构造平面直角坐标系，则点E的横坐标是（）

A、2- $\sqrt{2}$ B、 $\sqrt{2}$ -1 C、2- $\sqrt{3}$ D、 $\frac{1}{2}$

查看试题解析
5. 如图，直角坐标系中，O为原点，A（12，0），在等腰三角形ABO中，OB＝BA＝10，点B在第一象限，C为y轴正半轴上一动点，作以∠CBD为顶角的等腰三角形CBD，且∠CBD＝∠OBA，连接AD并延长与y轴交于点M（0，m），则m的值为（）.

A、 $\frac{7}{4}$ B、 $\frac{7}{3}$ C、 $\frac{7}{2}$ D、 $\frac{10}{3}$

查看试题解析

二、填空题

6. 如图，在△ABC中，∠ABC=90°， AB=BC，点B坐标为(-1，0)，点C坐标为(1，4)，则点A的坐标为.

查看试题解析
7. 如图，已知 $A (3, 0)$ ， $C (0, 6)$ ， $A C ⊥ B C$ ，且 $A C = B C$ ，则 $B$ 点的坐标为．

查看试题解析
8. 如图，在平面直角坐标系中，已知A（a，0），B（0，b）分别在坐标轴的正半轴上．设AB＝c. 当∠ABO的平分线经过点D（ $\sqrt{3}$ ， $- \sqrt{3}$ ），则a－b＋c的值为．

查看试题解析
9. 如图，在平面直角坐标系中，A(-1，2)，B(3，-2)，则三角形AOB的面积为.

查看试题解析
10. 如图，已知 $△ A B C$ 在平面直角坐标系中，在 $△ A B C$ 中， $A B = B C$ ， $∠ A B C = 90 °$ ．已知点 $A (0, - 8)$ ， $B (2, 0)$ ，点 $C$ 的坐标为．

查看试题解析
11. 在平面直角坐标系中，A（2，0），B（0，4），过点B作直线l $∥$ x轴，点P（a，4）是线l上的动点，以AP为边在AP右侧作等腰Rt∆APQ，使∠APQ＝90°.

(1)、当a＝0时，则点Q的坐标是.

(2)、当点P在直线1上运动时，点Q也随之运动，则OQ的最小值是.

查看试题解析
12. 如图，直线 $A B$ 与x轴，y轴分别交于点 $A (\sqrt{2} ， 0)$ 和 $B (0 ， - \sqrt{2})$ ，点P是直线 $A B$ 上的一个动点，点P的横坐标为 $t (0 \leq t \leq \sqrt{2})$ ，以线段 $O P$ 为边，点O为直角顶点在y轴右侧作等腰直角 $△ O P Q ， P Q$ 与x轴交于点C．在点P的运动过程中，当t的值 $=$ 时，△OCP为等腰三角形．

查看试题解析
13. 如图，已知点A的坐标为（m，0），点B的坐标为（m﹣2，0），在x轴上方取点C，使CB⊥x轴，且CB=2AO，点C，C′关于直线x=m对称，BC′交直线x=m于点E，若△BOE的面积为4，则点E的坐标为．

查看试题解析

三、解答题

14. 如图，在平面直角坐标系中，已知四边形 ABCD 各顶点的坐标分别为A(0，0)，B(9，0)，C(7，4)，D(2，8)，求四边形ABCD 的面积.

查看试题解析
15. 如图，在直角坐标系 $x O y$ 中，点 $A (0 ， 4)$ ，点B为x轴正半轴上一个动点，以 $A B$ 为边作 $△ A B C$ ，使 $B C = A B ， ∠ A B C = 90 °$ ，且点C在第一象限内．

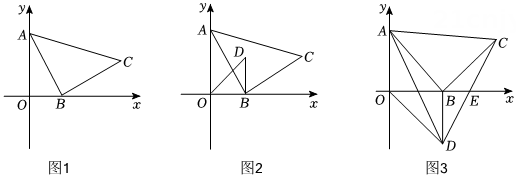(1)、如图1，若 $B (2 ， 0)$ ，求点C的坐标．

(2)、如图2，过点B向x轴上方作 $B D ⊥ O B$ ，且 $B D = B O$ ，在点B的运动过程中，探究点C，D之间的距离是否为定值．若为定值，求出该定值，若不是，请说明理由．

(3)、如图3，过点B向x轴下方作 $B D ⊥ O B$ ，且 $B D = B O$ ，连结 $C D$ 交x轴于点E，当 $△ A B D$ 的面积是 $△ B E C$ 的面积的2倍时，求 $O E$ 的长．

查看试题解析
16. 如图，在平面直角坐标系中， $A (m, 0)$ ， $B (0, n)$ ，满足 $(n - 4) ^{2} + |m + n| = 0$ ．点 $D$ 是 $x$ 轴上的动点且在点 $A$ 左侧，连结 $B D$ ，以 $B D$ 为边作 $△ B D E$ ，使 $∠ B D E = 90 °$ ， $B D = E D$ ，连结 $A B 、 E A$ ， $E A$ 交 $B D$ 于点 $G$ ．

(1)、求点 $A 、 B$ 的坐标；

(2)、如图1，若 $O A = A D$ ，求点 $E$ 的坐标；

(3)、如图2，试问动点 $D$ 在运动过程中，几何量 $A E - \sqrt{2} A D$ 的数值是否发生变化？如果不变，请求出这个定值；如果变化，请说明理由．

查看试题解析
17. 在平面直角坐标系 $x O y$ 中， $A (0, - 4), C$ 是 $x$ 轴上一点， $D$ 是 $y$ 轴上一点，

(1)、若 $C (- 2, 0), D (0, 1)$ ，判断 $△ A C D$ 的形状．

(2)、在（1）的条件下，延长 $C D$ 至 $B$ ，使 $C B = A C$ ，求点 $B$ 的坐标．

(3)、在（2）条件下，点 $E$ 是 $x$ 轴上的动点，若 $△ B C E$ 为等腰三角形，直接写出点 $E$ 的坐标．

(4)、如图，若 $A C ⊥ B C, A C = B C, A D$ 平分 $∠ B A C, D (0, a), B$ 的横坐标为 $b$ ，探究 $a$ 与 $b$ 的数量关系．

查看试题解析
18. 已知， $△ A B C$ 是等腰直角三角形， $B C = A B$ ， A点在x负半轴上，直角顶点B在y轴上，点C在x轴上方．

(1)、如图1所示，若A的坐标是 $(- 3 ， 0)$ ，点B的坐标是 $(0 ， 1)$ ，求点C的坐标；

(2)、如图2，过点C作 $C D ⊥ y$ 轴于D ，请写出线段 $O A$ ， $O D$ ， $C D$ 之间等量关系并说明理由；

(3)、如图3，若x轴恰好平分 $∠ B A C$ ， $B C$ 与x轴交于点E ，过点C作 $C F ⊥ x$ 轴于F ，问 $C F$ 与 $A E$ 有怎样的数是关系？并说明理由．

查看试题解析