平面直角坐标系规律题-浙教版数学八年级上册培优训练
试卷更新日期:2025-11-02 类型:复习试卷
一、选择题
-
1. 如图,直线 a⊥b ,在某平面直角坐标系中,x轴 ,y轴 ,点A的坐标为 ,点B的坐标为 ,则坐标原点为( )
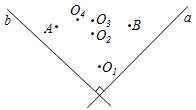 A、 B、 C、 D、2. 如图,在平面直角坐标系中,等腰直角三角形 OA1A2 的直角边 OA1 在 y轴的正半轴上,且 OA1=A1A2=1,以 OA2 为直角边作第二个等腰直角三角 形 OA₂ A3 , 以 OA3为直角边作第三个等腰直角三角OA3A4 , …,依此规律,得到等腰直角三角形 OA2017A2018 , 则点 A2017 的坐标为( )
A、 B、 C、 D、2. 如图,在平面直角坐标系中,等腰直角三角形 OA1A2 的直角边 OA1 在 y轴的正半轴上,且 OA1=A1A2=1,以 OA2 为直角边作第二个等腰直角三角 形 OA₂ A3 , 以 OA3为直角边作第三个等腰直角三角OA3A4 , …,依此规律,得到等腰直角三角形 OA2017A2018 , 则点 A2017 的坐标为( ) A、(0,21008) B、(21008 , 0) C、(0,21007) D、(21007 , 0)3. 如图,在平面直角坐标系中,已知点 ,A2在x轴的正半轴上,且 ,过点A2作 交y轴于点A3;过点A3作 交x轴于点A4;过点A4作 交y轴于点A5;过点A5作 交x轴于点A6;…按此规律进行下去,则点A2019的坐标是( )
A、(0,21008) B、(21008 , 0) C、(0,21007) D、(21007 , 0)3. 如图,在平面直角坐标系中,已知点 ,A2在x轴的正半轴上,且 ,过点A2作 交y轴于点A3;过点A3作 交x轴于点A4;过点A4作 交y轴于点A5;过点A5作 交x轴于点A6;…按此规律进行下去,则点A2019的坐标是( )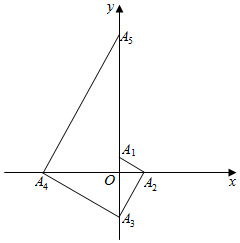 A、 B、 C、 D、4. 如图,直角坐标系中长方形的四个顶点坐标分别为 , , , , 点P从点A出发,沿长方形的边顺时针运动,速度为每秒2个长度单位,同时点Q从点A出发,沿长方形的边逆时针运动,速度为每秒3个长度单位,记P,Q在长方形边上第1次相遇时的点为 , 第二次相遇时的点为 , 第三次相遇时的点为 , ……,则点的坐标为( )
A、 B、 C、 D、4. 如图,直角坐标系中长方形的四个顶点坐标分别为 , , , , 点P从点A出发,沿长方形的边顺时针运动,速度为每秒2个长度单位,同时点Q从点A出发,沿长方形的边逆时针运动,速度为每秒3个长度单位,记P,Q在长方形边上第1次相遇时的点为 , 第二次相遇时的点为 , 第三次相遇时的点为 , ……,则点的坐标为( ) A、 B、 C、 D、5. 如图,点在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点 , 第2次接着运动到点 , 第3次接着运动到点…,按这样的运动规律,经过第2025次运动后动点的坐标是( )
A、 B、 C、 D、5. 如图,点在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点 , 第2次接着运动到点 , 第3次接着运动到点…,按这样的运动规律,经过第2025次运动后动点的坐标是( ) A、 B、 C、 D、6. 如图,一机器人从原点出发按图示方向作折线运动,第1次从原点到 , 第2次运动到 , 第3次运动到 , 第4次运动到 , 第5次运动到…则第2025次运动到的点的坐标是( )
A、 B、 C、 D、6. 如图,一机器人从原点出发按图示方向作折线运动,第1次从原点到 , 第2次运动到 , 第3次运动到 , 第4次运动到 , 第5次运动到…则第2025次运动到的点的坐标是( ) A、 B、 C、 D、7. 如图,在平面直角坐标系中有两条直线: ,对点 作如下操作.第 1 步,作点 关于 的对称点 ;第 2 步,作 关于 的对称点 ;第 3 步,再作 关于 的对称点 ;第 4 步,再作 关于 的对称点 以此类推,问:点 的坐标为( )
A、 B、 C、 D、7. 如图,在平面直角坐标系中有两条直线: ,对点 作如下操作.第 1 步,作点 关于 的对称点 ;第 2 步,作 关于 的对称点 ;第 3 步,再作 关于 的对称点 ;第 4 步,再作 关于 的对称点 以此类推,问:点 的坐标为( ) A、 B、 C、 D、8. 平面直角坐标系中,我们把横、纵坐标都是整数,且横、纵坐标之和大于的点称为“和点”.将某“和点”平移,每次平移的方向取决于该点横、纵坐标之和除以3所得的余数(当余数为时,向右平移;当余数为时,向上平移;当余数为时,向左平移),每次平移个单位长度.
A、 B、 C、 D、8. 平面直角坐标系中,我们把横、纵坐标都是整数,且横、纵坐标之和大于的点称为“和点”.将某“和点”平移,每次平移的方向取决于该点横、纵坐标之和除以3所得的余数(当余数为时,向右平移;当余数为时,向上平移;当余数为时,向左平移),每次平移个单位长度.例:“和点”按上述规则连续平移3次后,到达点 , 其平移过程如下:
若“和点”按上述规则连续平移次后,到达点 , 则点的坐标为( )
A、或 B、或 C、或 D、或9. 在平面直角坐标系上有个点 , 点P第1次向上跳动1个单位至点 , 紧接着第2次向左跳动2个单位至点 , 第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第2024次跳动至的坐标是( ) A、 B、 C、 D、10. 如图,动点A在平面直角坐标系中按图中方向运动,第一次从原点出发,依次运动到点 , , , , , …像这样的运动规律,点的横坐标是( )
A、 B、 C、 D、10. 如图,动点A在平面直角坐标系中按图中方向运动,第一次从原点出发,依次运动到点 , , , , , …像这样的运动规律,点的横坐标是( ) A、 B、 C、 D、11. 在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右、向上、向右、向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1 , 第2次移动到A2 , …,第n次移动到An,则△OA2A2018的面积是( ).
A、 B、 C、 D、11. 在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右、向上、向右、向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1 , 第2次移动到A2 , …,第n次移动到An,则△OA2A2018的面积是( ). A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
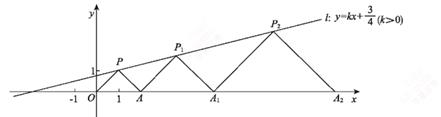
12. 如图,在平面直角坐标系中,点A,A1 , A2 , ……在工轴上,点P,P1 , P2 , 在直线l:y=kx+ (k>0)上,∠OPA=90°,点P(1,1) ,A(2,0),且AP1 , A1P2 , ……均与OP平行,A1P1 , A2P2 , ……均与AP平行,则有下列结论:①直线AP1的函数解析式为y=x-2;②点P2的纵坐标是 ;③点P2021的纵坐标为( )2021。其中正确的是(填序号)。
 13. 在平面直角坐标系中,对于任意三点A、B、C的“矩面积”,给出如下定义:“水平底” :任意两点横坐标差的最大值,“铅垂高” :任意两点纵坐标的最大值,则“矩面积” .例如:三点坐标分别为A(1,2)、B(-3,1)、C(2,-2),则“水平底” =5,“铅垂高” =4,“矩面积”S=20.若D(1,2)、E(-2,1),F(0,t )三点的“矩面积”S=15,则的 值为.14. 如图:将边长为1的正三角形OAP,沿x轴正方向连续翻转若干次,点A依次落在点A1 , A2 , A3 , A4 , …,A2019的位置上,则点A2019的坐标为.
13. 在平面直角坐标系中,对于任意三点A、B、C的“矩面积”,给出如下定义:“水平底” :任意两点横坐标差的最大值,“铅垂高” :任意两点纵坐标的最大值,则“矩面积” .例如:三点坐标分别为A(1,2)、B(-3,1)、C(2,-2),则“水平底” =5,“铅垂高” =4,“矩面积”S=20.若D(1,2)、E(-2,1),F(0,t )三点的“矩面积”S=15,则的 值为.14. 如图:将边长为1的正三角形OAP,沿x轴正方向连续翻转若干次,点A依次落在点A1 , A2 , A3 , A4 , …,A2019的位置上,则点A2019的坐标为. 15. 如图所示,在平面直角坐标系中, , , , …都是等边三角形,其边长依次为2,4,6,…其中点的坐标为 , 点的坐标为 , 点的坐标为 , 点的坐标为 , …,按此规律排下去,则点的坐标为 .
15. 如图所示,在平面直角坐标系中, , , , …都是等边三角形,其边长依次为2,4,6,…其中点的坐标为 , 点的坐标为 , 点的坐标为 , 点的坐标为 , …,按此规律排下去,则点的坐标为 . 16. 如图,在平面直角坐标系中,已知点A的坐标是 , 以为边在右侧作等边三角形 , 过作x轴的垂线,垂足为点 , 以为边在右侧作等边三角形 , 再过点作x轴的垂线,垂足为点 , 以为边在右侧作等边三角形 , …,按此规律继续作下去,得到等边三角形 , 则点的纵坐标为
16. 如图,在平面直角坐标系中,已知点A的坐标是 , 以为边在右侧作等边三角形 , 过作x轴的垂线,垂足为点 , 以为边在右侧作等边三角形 , 再过点作x轴的垂线,垂足为点 , 以为边在右侧作等边三角形 , …,按此规律继续作下去,得到等边三角形 , 则点的纵坐标为 17. 如图,在平面直角坐标系中,点A1 , A2 , A3…都在x轴上,点B1 , B2 , B3…都在直线 上,△OA1B1 , △B1A1A2 , △B2B1A2 , △B2A2A3 , △B3B2A3…都是等腰直角三角形,且OA1=1,则点B2019的坐标是.
17. 如图,在平面直角坐标系中,点A1 , A2 , A3…都在x轴上,点B1 , B2 , B3…都在直线 上,△OA1B1 , △B1A1A2 , △B2B1A2 , △B2A2A3 , △B3B2A3…都是等腰直角三角形,且OA1=1,则点B2019的坐标是. 18. 如图,在平面直角坐标系中,点在直线上,过点作轴,交直线于点B,以为直角顶点,为直角边,在的右侧作等腰直角三角形;再过点作轴,分别交直线和于 , 两点,以为直角顶点,为直角边,在的右侧作等腰直角三角形…按此规律进行下去,点的横坐标为 .
18. 如图,在平面直角坐标系中,点在直线上,过点作轴,交直线于点B,以为直角顶点,为直角边,在的右侧作等腰直角三角形;再过点作轴,分别交直线和于 , 两点,以为直角顶点,为直角边,在的右侧作等腰直角三角形…按此规律进行下去,点的横坐标为 . 19. 如图,过点A1(1,0)作x轴的垂线,交直线y=2x于点B1;点A2与点O关于直线A1B1对称;过点A2(2,0)作x轴的垂线,交直线y=2x于点B2;点A3与点O关于直线A2B2对称;过点A3(4,0)作x轴的垂线,交直线y=2x于点B3;…,按此规律作下去,则点Bn的坐标为 .
19. 如图,过点A1(1,0)作x轴的垂线,交直线y=2x于点B1;点A2与点O关于直线A1B1对称;过点A2(2,0)作x轴的垂线,交直线y=2x于点B2;点A3与点O关于直线A2B2对称;过点A3(4,0)作x轴的垂线,交直线y=2x于点B3;…,按此规律作下去,则点Bn的坐标为 .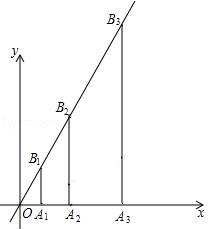 20. 如图所示,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…,那么点A4n+1(n为自然数)的坐标为(用n表示).
20. 如图所示,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…,那么点A4n+1(n为自然数)的坐标为(用n表示).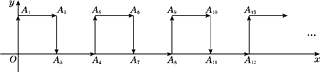 21. 如图,在平面直角坐标系中,将 绕点 顺时针旋转到 的位置,使点 的对应点 落在直线 上……,依次进行下去,若点 的坐标是(0,1),点 的坐标是 ,则点 的横坐标是.
21. 如图,在平面直角坐标系中,将 绕点 顺时针旋转到 的位置,使点 的对应点 落在直线 上……,依次进行下去,若点 的坐标是(0,1),点 的坐标是 ,则点 的横坐标是.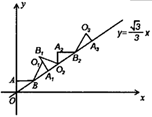 22. 如图,在平面直角坐标系中,已知点 , 点P,点Q分别从点A,点C同时出发,沿长方形的边作环绕运动,点P按逆时针方向以每秒2个单位长度的速度匀速运动,点Q按顺时针方向以每秒3个单位长度的速度匀速运动,则第2023秒P,Q两点相遇地点的坐标是 .
22. 如图,在平面直角坐标系中,已知点 , 点P,点Q分别从点A,点C同时出发,沿长方形的边作环绕运动,点P按逆时针方向以每秒2个单位长度的速度匀速运动,点Q按顺时针方向以每秒3个单位长度的速度匀速运动,则第2023秒P,Q两点相遇地点的坐标是 . 23. 数学家高斯推动了数学科学的发展,被数学界誉为“数学王子”,据传,他在计算1+2+3+4+⋯+100时,用到了一种方法,将首尾两个数相加,进而得到1+2+3+4+⋯+100= . 人们借助于这样的方法,得到1+2+3+4+⋯+n=(n是正整数).有下列问题,如图,在平面直角坐标系中的一系列格点Ai(xi , yi),其中i=1,2,3,⋯,n , ⋯,且xi , yi是整数.记an=xn+yn , 如A1(0,0),即a1=0,A2(1,0),即a2=1,A3(1,-1),即a3=0,⋯,以此类推.则a2023= .
23. 数学家高斯推动了数学科学的发展,被数学界誉为“数学王子”,据传,他在计算1+2+3+4+⋯+100时,用到了一种方法,将首尾两个数相加,进而得到1+2+3+4+⋯+100= . 人们借助于这样的方法,得到1+2+3+4+⋯+n=(n是正整数).有下列问题,如图,在平面直角坐标系中的一系列格点Ai(xi , yi),其中i=1,2,3,⋯,n , ⋯,且xi , yi是整数.记an=xn+yn , 如A1(0,0),即a1=0,A2(1,0),即a2=1,A3(1,-1),即a3=0,⋯,以此类推.则a2023= .
三、解答题
-
24. 在平面直角坐标系中,对于点P(x,y),我们把点叫作点P的前进点.已知点A1的前进点为A2 , 点A2的前进点为A3 , 点A3的前进点为A4……这样依次得到点A1 , A2 , A3 , A4 , …,Aₙ.(1)、若点A1的坐标为(3,1),写出点A2 , A3 , A4 , A5的坐标.(2)、从第(1)题的解答中,你发现了什么规律?按此规律,写出A2021的坐标.(3)、若点A1的坐标为(a,b),对于任意的正整数n,点A,均在x轴上方,则a,b应满足什么条件?25. 如图,在直角坐标系中,第一次将△OAB变换成△OA1B1 , 第二次将△OA1B1变换成△OA2B2 , 第三次将△OA2B2变换成
 (1)、观察每次变换前后三角形的变化规律,按此变化规律,将△OA3B3变换成△OA4B4 , 则A4的坐标是 , B4的坐标是.(2)、按第(1)题找到的规律,将△OAB进行n次变换,得到△OAₙBₙ.
(1)、观察每次变换前后三角形的变化规律,按此变化规律,将△OA3B3变换成△OA4B4 , 则A4的坐标是 , B4的坐标是.(2)、按第(1)题找到的规律,将△OAB进行n次变换,得到△OAₙBₙ.①推测A。的坐标是 ▲ , B。的坐标是 ▲ .
②求△OAₙBₙ的面积S.