平面直角坐标系两点距离公式的应用-浙教版数学八年级上册培优训练

试卷更新日期：2025-11-02 类型：复习试卷

进入出卷网下载

一、选择题

1. 已知 $A (2, a)$ ， $B (b, - 3)$ 是平面直角坐标系上的两个点， $A B ∥ x$ 轴，且点B在点A的右侧．若 $A B = 5$ ，则（）

A、 $a = - 3$ ， $b = - 3$ B、 $a = - 3$ ， $b = 7$ C、 $a = 2$ ， $b = 2$ D、 $a = - 8$ ， $b = 2$

查看试题解析
2. 点 $P (3 ， - 4)$ 到原点的距离为（）

A、5 B、4 C、3 D、 $- 3$

查看试题解析
3. 已知 $A (- 2 ， 4) ， B (2 ， 4)$ ，那么线段AB的长度是（）

A、4 B、6 C、8 D、无法确定

查看试题解析
4. 在平面直角坐标系中，点A(-5，6)，B(3，-4)，经过点A 的直线a与x轴平行，如果点 C 是直线a上的一个动点，那么当线段 BC 的长度最短时，点C 的坐标为( )

A、(6，3) B、(-4，-5) C、(3，6) D、(-5，-4)

查看试题解析
5. 如图，在平面直角坐标系中， $A (- 1, 1)$ ， $B (- 1, - 2)$ ， $C (3, - 2)$ ， $D (3, 1)$ ，一只瓢虫从点A 出发以2个单位长度/秒的速度沿 $A \to B \to C \to D \to A$ 循环爬行，问第2022秒瓢虫在（）处．

A、 $(1, 1)$ B、 $(- 1, - 2)$ C、 $(1, - 2)$ D、 $(3, - 2)$

查看试题解析
6. 在平面直角坐标系内有一点 $A (2, - 1)$ ， $O$ 为原点， $P$ 是坐标轴上的一个动点，若以点 $P$ 、 $O$ 、 $A$ 为顶点的三角形是等腰三角形，则符合条件的动点 $P$ 的个数为（）

A、 $8$ B、 $6$ C、 $4$ D、 $2$

查看试题解析
7. 如图，直线 $y = k x + 6$ 过点 $A (1, a)$ ，且与 $x$ 轴交于点 $B (2, 0)$ ，点 $C$ 是 $y$ 轴上的一个动点，则 $△ A B C$ 的周长的最小值是（）

A、 $3 \sqrt{2} + \sqrt{10}$ B、 $3 \sqrt{3} + \sqrt{10}$ C、 $5 \sqrt{2} + 3 \sqrt{5}$ D、 $3 \sqrt{5} + 2 \sqrt{10}$

查看试题解析
8. 在平面直角坐标系 $x O y$ 中，点 $A (0 ， a)$ ， $B (b ， 24 - b)$ ， $C (2 a - 3 ， 0)$ ， $0 < a < b < 24$ ，若 $∠ A O C$ 的对称轴是直线 $O B$ ，且 $A B = B C$ ，则 $a + b$ 的值为（　　）

A、15或21 B、9或11 C、15或20 D、15或19

查看试题解析

二、填空题

9. 在直角坐标平面中，已知 $A (- 2, a)$ ， $B (1, a)$ ，那么 $A B =$ ．

查看试题解析
10.

(1)、如图①，在平面直角坐标系中，M是直线y=-x上的动点，过点M作MN⊥x轴，交直线y=x于点N，当MN≤8时，设点 M 的横坐标为m，则m 的取值范围为.

(2)、如图②，有一种动画程序，屏幕上正方形区域ABCD 表示黑色物体甲，其中A(1，1)，B(2，1)，C(2，2)，D(1，2)，用信号枪沿直线y=2x+b发射信号，当信号遇到区域甲时，甲由黑变白，则b的取值范围为时，甲能由黑变白.

查看试题解析
11. 如图，在 $Rt △ A B C$ 中， $∠ C = 90 °$ ， $A C = 2$ ， $B C = 3$ ．将 $△ A B C$ 沿射线 $C B$ 平移得到 $△ A^{'} B^{'} C^{'}$ ，将 $A B$ 绕着点 $A$ 逆时针旋转 $90 °$ 得到线段 $A D$ ，连接 $D A^{'}$ ， $D B^{'}$ 在 $△ A B C$ 的平移过程中， $△ A^{'} B^{'} D$ 的周长的最小值为．

查看试题解析
12. 五个边长为 1 的正方形如图摆放在平面直角坐标系中，过 $(a, 0), (3, 3)$ 的一条直线将这五个正方形分成面积相等的两部分，则 $a$ 的值是.

查看试题解析
13. 如图，在平面直角坐标系中， $△ A B C$ 的顶点坐标分别为 $A (- 4 ， 1)$ ， $B (0 ， 5)$ ， $C (0 ， 1)$ ，点 $D$ 与点 $A$ 关于 $y$ 轴对称，连接 $B D$ ，在边 $A B$ 上取一点 $E$ ，在 $B D$ 的延长线上取一点 $F$ ，并且满足 $A E = D F$ ，连接 $E F$ 交边 $A D$ 于点 $G$ ，过点 $G$ 作 $E F$ 的垂线交 $y$ 轴于点 $H$ ，则点 $H$ 的坐标为

查看试题解析

三、解答题

14. 【阅读理解】
我们知道，任意两点关于它们所连线段的中点成中心对称，在平面直角坐标系中，任意两点 $P (x_{1}, y_{1})$ ， $Q (x_{2}, y_{2})$ 的对称中心的坐标为 $(\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2})$
【观察应用】
（1）如图，在平面直角坐标系中，若点 $P_{1} (0, - 1)$ ， $P_{2} (2, 3)$ 的对称中心是点 $A$ ，则点 $A$ 的坐标为；
（2）另取两点 $B (- 1.6, 2.1)$ ， $C (- 1, 0)$ ．有一电子青蛙从点 $P_{1}$ 处开始依次关于点A，B，C做循环对称跳动，即第一次跳到点 $P_{1}$ 关于点A的对称点 $P_{2}$ 处，接着跳到点 $P_{2}$ 关于点B的对称点 $P_{3}$ 处，第三次再跳到点 $P_{3}$ 关于点C的对称点 $P_{4}$ 处，第四次再跳到点 $P_{4}$ 关于点A的对称点 $P_{5}$ 处，……则 $P_{3}$ ， $P_{8}$ 的坐标分别为；
【拓展延伸】
（3）求出点 $P_{2023}$ 的坐标，并直接写出在x轴上与点 $P_{2023}$ ，点 $C$ 构成等腰三角形的点的坐标．

查看试题解析
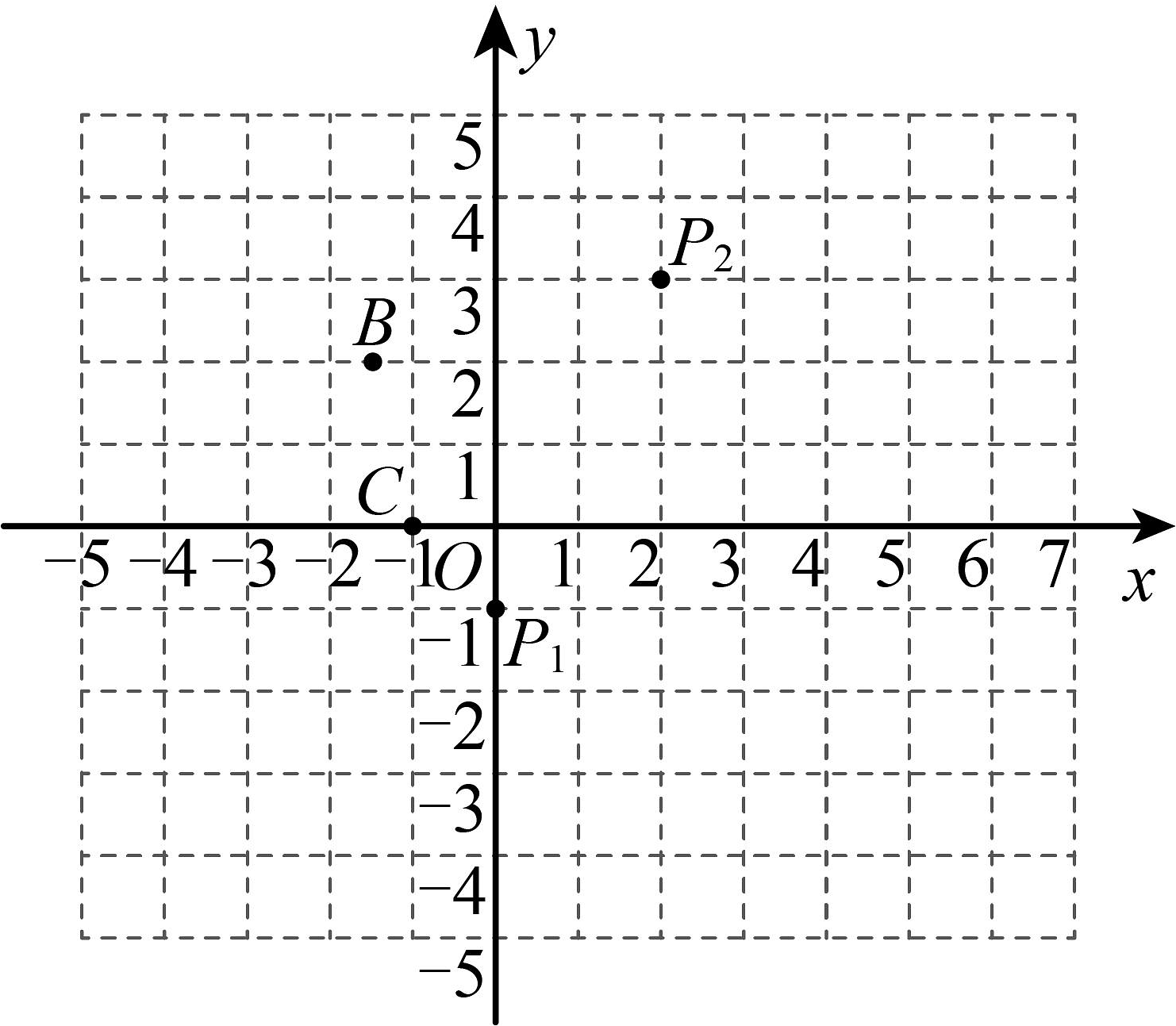15. 阅读下列一段文字，然后回答下列问题．已知在平面内两点 $P_{1} (x_{1}, y_{1})$ 、 $P_{2} (x_{2}, y_{2})$ ，其两点间的距离 $P_{1} P_{2} = \sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}}$ 同时，当两点所在的直线在坐标轴或平行于坐标轴时，两点间距离公式可简化为 $P_{1} P_{2} = |x_{2} - x_{1}|$ 或 $P_{1} P_{2} = |y_{2} - y_{1}|$ ．

(1)、已知 $A (- 2, 3)$ 、 $B (4, - 5)$ ，试求A、B两点间的距离；

(2)、已知A、B在平行于y轴的直线上，点A的纵坐标为6，点B的纵坐标为 $- 2$ ，试求A、B两点间的距离．

(3)、已知一个三角形各顶点坐标为 $A (0, 6)$ 、 $B (- 3, 2)$ 、 $C (3, 2)$ ，请判定此三角形的形状，并说明理由．

(4)、已知一个三角形各顶点坐标为 $A (- 1, 3)$ 、 $B (0, 1)$ 、 $C (2, 2)$ ，请判定此三角形的形状，并说明理由．

查看试题解析
16. 【定义理解】在平面直角坐标系中，有 $A (m, 0)$ ， $B (0, n)$ 两点，若存在点C使得 $∠ A B C = 90 °$ ，且 $A B = B C$ ，则称点 $C$ 为m的“等垂点”．
例如：在 $A (1, 0)$ ， $B (0, 1)$ ， $C (- 1, 0)$ 三点中，因为 $∠ A B C = 90 °$ ，且 $A B = B C$ ，所以点C为1的“等垂点”．
【探究应用】
（1）点 $A (2, 0)$ ， $B (0, 2)$ ，则 $C (2, 4)$ ____________2的“等垂点”（填“是”或“不是”）．
（2）如图1，若点 $A (4, 0)$ ， $B (0, 3)$ ，则点 $C$ 是4的“等垂点”，则点 $C$ 的坐标为____________．
（3）如图2，若一次函数 $y = 3 x - 5$ 上存在5的“等垂点”，求5的“等垂点”C 的坐标．
【拓展提升】
（4）若在直线 $y = k x + b (k > 0)$ 上存在无数个5的“等垂点”，且直线 $y = k x + b (k > 0)$ 与x轴交于点E，与y轴交于点F，点M在线段 $E F$ 上，点 $P$ 在 $△ E O F$ 内， $E P = 4$ ， $O P = 3$ ，连接 $M P$ ，设 $E M = a$ ，直接写出 $△ E P M$ 面积 $S$ 关于a的表达式．

查看试题解析